夹层板大挠度问题的力学表征与数值模拟

李 伟，靳诚忠，刘思远

(沈阳飞机设计研究所 综合强度部，沈阳 110035)

夹层板大挠度问题的力学表征与数值模拟

李 伟，靳诚忠，刘思远

(沈阳飞机设计研究所 综合强度部，沈阳 110035)

随着材料制备工艺的发展和成型加工技术的日趋完善，夹层板在现代航空领域结构设计中获得了广泛应用，以获得理想的重量及其它功能性指标，工程分析时往往利用薄板理论进行近似分析，这忽略了夹层板的良好的抗弯特性，给分析结果带来较大误差。在薄板大挠度问题及夹层板相关理论的基础上，提出分段叠加法分析大挠度夹层板的变形机理，并利用有限元进行了数值模拟，结合某型飞机蜂窝轮舱壁板静力试验验证了夹层板大挠度变形机理的合理性，证明了叠加法的有效性。

飞行器设计；夹层板；大挠度；分段叠加法

近年来随着空天领域的迅猛发展，使得飞行器对结构材料的要求更为严格：在减轻结构重量的同时还要满足承载的要求(超轻质、高比强度、高比刚度)以及多功能性[1-2](散热、电磁屏蔽、致动等)，这使夹层板(蜂窝夹芯版或点阵夹芯板)广为应用，同时随着航空宇航设计理念的发展，飞行器的新颖结构进一步对夹层板壳的结构与材料提出了新的要求。非线性理论问题、各向异性材料问题等都成为进行深入研究的重要课题。早在50年前，Reissner[3]首先建立了具有软夹芯和极薄表层的夹层矩形板的大挠度理论，此时视表层如薄膜一样，忽略了表层的抗弯刚度。在此基础上刘人怀[4-5]进一步建立了夹层圆板和矩形板的更为精确的非线性弯曲理论。目前工程分析时主要将夹层板等效为均质板，利用中面应力代替表层应力进行强度计算。试验表明给方法误差较大。Tagarielli和Fleck[6]夹层材料三点弯曲梁的失效模式，本文结合利用夹层板特性结合薄板大挠度理论提出大挠度夹层板在载荷作用下变形/失效机理，利用有限元进行数值验证，提出大变形分析方法。大变形分析方法及失效均经过试验验证，并与工程分析结果进行对比，计算误差降低明显，该方法对于对夹层板设计具有重要的意义。

1 工程中夹层板的计算方法

夹层结构的设计思想与工字梁相似，即主要承载的面板起缘条作用，而夹芯主要承受剪应力，起着腹板的作用。在夹层结构的理论研究中，已提出过不少的计算模型。仅就线性理论来说，大概有以下几种计算模型：(1)Reissner理论：将表层薄板看作为薄膜，即认为它只承受平面力，忽略了其本身的抗弯刚度，夹芯则认为只承受剪切作用；(2)Hoff理论[7]：将表层看作为普通的薄板，考虑了本身的抗弯刚度，不仅考虑了面板沿厚度均匀分布的平面力，同时也考虑沿厚度程线性变化的非均匀分布力，夹芯只承受剪切作用；(3)波鲁沙科夫(Прусаков)-杜庆华理论:将面板看做普通薄板,夹芯除了承受剪切外还考虑夹芯存在的横向弹性变形的作用。工程中并未利用上述理论获得精确解而通常近似地将夹层板简化为具有等效弯曲刚度与等效平面拉压刚度的均质板，在同样边界条件下计算板中的内力与力矩，然后按面板承受正应力而夹芯只承受横向剪应力的原则求取夹层板中各点应力。具有等效弯曲刚度与等效平面拉压刚度的均质板，其板厚teq与弹性模量Eeq，泊松比μeq可按下式确定。

(1)

(2)

(3)

其中E1,E2为面板弹性模量，μ1,μ2分别为为面板材料泊松比，t1,t2为面板厚度，h为夹芯厚度。

在两块面板完全相同时板中心挠度：

(4)

板中心面板应力：

(5)

(6)

其中m1,m2,m3为与夹层板长宽比有关的修正系数。

2 分段叠加法分析大挠度夹层板变形机理

牛春匀[8]指出板可以看成二维梁结构，在横向载荷作用下，板发生弯曲变形，并产生剪应力，但不会在中性面上产生正应力，对于很薄的板或者膜板由于变形后板的曲率和变形很大，产生薄膜应力以平衡横向载荷。

结合夹层板特点提出分段叠加法认为面外载荷作用下板壳变形属几何非线性范畴，其结构响应分为三个阶段，即：弹性弯曲阶段，弹性弯曲向膜力作用的转换阶段，膜力阶段。弹性弯曲阶段板自身刚度为主导，体现出线性特征，随着载荷增加，板壳变形进一步增加，板中心非线性的薄膜力为主导，板壳变形机理如图1所示其中过渡阶段与板件的剪切性能、横向承载能力、厚度及相对宽度(几何尺寸)等参数有关。

图1 分段叠加法分析板的变形机理

对于面板应力则可以表述为：

(7)

3 大挠度夹层板变形机理的数值模拟及试验验证

某型飞机轮舱壁板为铝蜂窝夹层结构，厚度为19.6 mm，上下面板厚度t=0.8 mm，芯体为铝蜂窝材料，结构简图如图2所示。壁板载荷为沿两个方向线性变化的气动吸力，试验时板中心处位移为14.95 mm，属于大挠度夹层板问题。刘人怀[3]应用幂级数法给出了均布载荷作用下具有不同边界条件的夹层圆板的大挠度问题的精确解，而对于矩形夹层板尤其在非均匀载荷作用下则很难给出精确解。

图2 某型飞机蜂窝夹芯壁板结构简图

数值计算方法目前被广泛地应用于那些数学方程比较复杂，物理边界形状(载荷)又不规则的问题，本文则利用有限元软件对分段叠加法给出的变形机理及应力计算过程进行验证。数值模拟过程中将面板看做普通薄板,夹芯除了承受剪切外还考虑夹芯横向弹性变形的作用。利用有限元进行了2种求解：1是线性求解，2是几何非线性(大挠度)，2种算法位移云图如图3所示,计算与试验结果对比如表1和表2所示，几何非线性计算与试验测量板中心挠度对比如图4所示。

图3 有限元线性计算与非线性计算位移云图

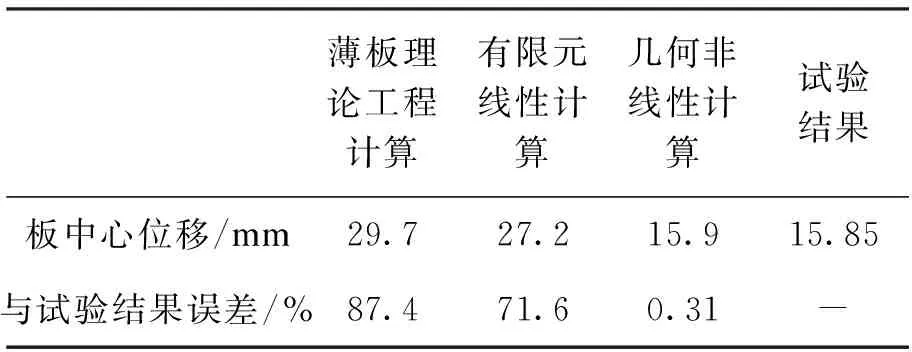
表1 不同算法壁板中心位移与试验测量结果对比

图4 几何非线性计算位移与试验测量结果对比

表2 不同算法面板中心最大主应力与试验测量结果对比

通过不同算法与试验结果对比可以发现：(1)薄板理论工程算法及有限元线性计算应力与试验结果误差较大，说明壁板变形已超出弹性范畴；(2)几何非线性计算应力与试验实测应力基本一致，证明了叠加法计算大挠度夹层板应力的有效性；(3)几何非线性计算挠度与试验测量位移基本一致，说明该型飞机轮舱壁板已经出现几何非线性特征，处于弹性变形向大挠度变形转换阶段，变形机理分析合理。

4 结论

本文基于经典板壳理论提出面外载荷作用下夹层板的变形机理属几何非线性范畴，结合薄板大挠度及夹层板相关理论的基础上，利用分段叠加法分析大挠度夹层板的变形及应力状态。利用有限元进行了数值模拟，结合某型飞机蜂窝轮舱壁板静力试验验证了夹层板大挠度变形机理的合理性，证明了叠加法的有效性，为该类结构在空天领域的应用提供理论支持。

[1]Gibson L J,Ashby M F.Cellular solids:structure and properties[M].2nd edition.Cambridge:Cambridge University Press,1997.

[2]杨亚政，杨嘉陵，曾涛，等.轻质多孔材料研究进展[J].力学季刊，2007,28(4):503-516.

[3]Reissner,E.Finite deflection of sandwich plate[J].J Aeron Sci,1950,17(2):125-130.

[4]刘人怀.夹层圆板大挠度问题的精确解[J].应用数学和力学，1982，3(1):11-23.

[5]刘人怀.夹层圆板的非线性弯曲[J].应用数学和力学，1981，2(2):173-191.

[6]Tagarielli V L,Fleck N A.Deshpande V S.Collapse of clamped and simply supported composite sandwich beams in three-point bending[J].Composites:Part B,2004(35):523-534.

[7]Hoff N J.Bending and buckling of rectangular sandwich plates[R].NACA TN-2225,1950.

[8]牛春匀.使用飞机结构应力分析及尺寸设计[M].北京：北京航空工业出版社，2009.

(责任编辑：宋丽萍 英文审校：刘敬钰)

Mechanicalperformanceandnumericalsimulationofsandwichplatewithlargedeflection

LI Wei，JIN Cheng-zhong，LIU Si-yuan

Integrated Stress Department，Shenyang Aircraft Design & Research Institute,Shenyang 110035)

With the development of material manufacturing techniques and the gradual perfection of contour processing technology,sandwich plates have been widely used in modern aircraft structure design to obtain ideal weight and other functional indicators.The thin plate theory is often used in engineering approximate analysis,which ignores the good bending characteristics of sandwich plates and brings large errors to the analytical results.Based on the large deflection problem of thin plates and related theories of sandwich plates,the method of subsection superposition is proposed to analyze the deformation mechanism of the large deflection of sandwich plates,which is simulated numerically by finite element.Combining the static test of certain type of aircraft honeycomb sandwich compartment panel,the paper verifies the rationality of deformation mechanism and proves the effectiveness of the superposition method.

aircraft design;sandwich plate;large deflection;method of subsection superposition

2013-10-12

李伟(1979-)，男，辽宁义县人，工程师，主要研究方向：飞机强度设计，E-mail:liweidlut@aliyun.com。

2095-1248(2014)01-0024-04

O342; V215.5

A

10.3969/j.issn.2095-1248.2014.01.006