超音速气流中受热壁板的非线性颤振特性

王广胜，杨晓东

(1.沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136；2.北京工业大学 机电工程学院，北京 100124)

超音速气流中受热壁板的非线性颤振特性

王广胜1，杨晓东2

(1.沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136；2.北京工业大学 机电工程学院，北京 100124)

随着高速飞行器技术的快速发展，壁板热颤振成为国内外研究人员的关注热点。壁板热颤振对飞行器性能有重大影响，甚至影响飞行安全。以超音速气流下的无限展长二维壁板结构作为研究对象，计入热效应的影响，根据Kirchhoff平板理论和Von Karman大变形几何非线性壁板理论建立系统的运动微分方程。并以壁板在x=0.25处为算例绘制了其前三阶弯曲构型的静态分岔图，对不同轴向载荷条件下壁板的屈曲构型进行了分析。考虑到温差ΔT是影响热应力的重要因素，对比了不同温差条件下，壁板的静气动弹性变形图，结果表明，温差越大，壁板偏离静平衡位置的位移越大。

一般力学；热颤振；壁板颤振；超音速气流；气动热效应

随着超音速飞行器技术的飞速发展，飞行器的飞行马赫数越来越高。对于高马赫数(一般大于2.2)飞行的飞行器，由于超音速和高超音速的气流绕经飞行器，气流受强烈的压缩作用将会导致温度的升高，而且边界层内的剧烈摩擦作用也将会使气体温度大大升高，从而导致飞行器结构温度升高。所以，对于此类飞行器在颤振设计中需考虑气动加热的影响，壁板的热颤振问题成为一个很重要的气动弹性问题。

气动加热产生的温度效应对壁板颤振特性的影响主要体现在以下两个方面[1]：(1)材料的机械性能将会随着温度的升高而发生改变。例如，材料的弹性模量会随着温度的升高而降低。(2)结构热应力将会在温度分布不均处或者结构变形受到约束的地方产生。由于材料性能的变化和结构热应力的存在，颤振边界和颤振特性将会产生变化，从而影响飞行器的性能甚至飞行安全。

Houbolt早在1958年首次研究了均匀分布温度场下二维壁板的颤振特性，建立了相关的控制方程，并对二维壁板的颤振边界以及屈曲失稳特性进行了研究分析[2]。1976年Yang和Han采用有限元方法研究了相同温度场条件下二维壁板的热屈曲颤振问题[3]。Xue和Mei将温度效应以热应力的形式引入到板结构的动力学方程中，从而比较直观和简便地把复杂的温度分布情况模拟出来。并用有限元法分析了超音速气流中任意温度下非线性壁板颤振问题[4]以及在温度影响下二维壁板的颤振响应和疲劳寿命[5]。目前有关壁板热颤振的研究大多集中于平板的颤振问题，但是也有部分文献研究了带有初始几何曲率壁板的热颤振问题。Ghoman和Azzouz在2008年到2009年分别运用时域和频域方法研究了曲壁板在存在热载荷时的非线性颤振特性，指出曲壁板不会出现热屈曲[6-7]。在国内，张蕊丽等对曲壁板的非线性热颤振问题进行了初步探究[8]。2012年，杨智春等应用数值求解的方法研究了带初始几何曲率的二维各向同性材料壁板的非线性热颤振特性[9]。

热效应对结构气动弹性特性的影响非常复杂，陈文俊总结了前人的研究成果，归纳出了11条结论[10]。但是，在目前的研究现状下，不可能同时兼顾所有这些因素，目前在研究中所采用的是两个简化假设：(1)温度场不受结构变形的影响；(2)相对于颤振的响应时间来说，温度变化是一个很缓慢的过程。本文在计入热效应的条件下，推导了两端简支二维壁板的振动微分方程，并通过具体算例得出了壁板前三阶弯曲构型的静态分岔图，而且对比了不同温差下壁板的屈曲程度。

1 二维壁板在超音速流下的控制方程

建立二维壁板在超音速气流中的力学模型，如图1所示，考虑壁板受温度变化ΔT影响下的简支无限展长的壁板模型，其长度为L，厚度为h，密度为ρ，在其上表面有沿x方向的超音速气流，流速为U∞，马赫数为M∞，空气密度为ρ∞。

图1 二维壁板在超音速气流中的力学模型

仅考虑板的横向振动，采用Von Karman大变形几何非线性壁板理论，应变位移关系表示为[11]：

(1)

应力为：

(2)

(3)

由Kirchhoff平板理论可以得到壁板的振动方程为：

(4)

其中，w为壁板在z方向的位移，Nx为面内力，Mx为弯矩，qa是气动载荷。由此可计算单位长度壁板的面内力：

(5-a)

(5-b)

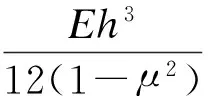
(6)

由于二维壁板的两端都有约束，位移边界条件为w|x=0,L=0，故：

(7)

由于面内力为常数，对其沿x向取平均并由式(7)可得：

(8)

在壁板颤振的超音速、高超音速非定常气动力的计算中，目前广泛采用形式简单且具有较好的精度活塞理论[13]，当来流马赫数较小时，一般采用一阶线性活塞理论便可以较准确地计算系统的气动力，其表达式为：

(9)

其中ξ，η分别表示气动刚度系数和气动阻尼系数。

(10)

其中ρ∞、U∞和M∞为自由流密度、来流速度和马赫数。

整理化简(6)式并做无量纲化处理，可得系统的振动方程为：

(11)

超音速气流中的二维壁板受气动热的影响，会在热载荷的作用下产生静气动弹性变形，为了研究两端简支的二维壁板静气动弹性变形，将上述控制方程去掉时间相关项、阻尼项和强迫项，可得：

(12)

2 二维壁板平衡构型计算

用Ψ(x)表示去掉时间相关项后的w(x,t)，表示二维壁板的屈曲构型，由式(11)可得：

(13)

两端简支的二维壁板的边界条件为：

Ψ|x=0,1=0,Ψ″|x=0,1=0

(14)

将式(14)中的积分项记为由Ψ(x)确定的常数，令

(15)

其中Γ为常数，故式(14)可写为：

Ψ(4)+(P-Γ)Ψ″=0

(16)

上式可记为：

Ψ(4)+λ2Ψ″=0

(17)

其中

λ2=P-Γ

(18)

式中λ2是表征临界屈曲载荷的特征值。

将式(16)代入式(19)可得

(19)

方程(18)的通解[12]为：

Ψ(x)=c1+c2x+c3cosλx+c4sinλx

(20)

将(16)式代入边界条件式(13)中，可得方程组：

(21)

由式(20)的行列式可得特征方程为：

csinλ=0或λ=mπ

(22)

故壁板的屈曲构型为：

Ψ(x)=csin(mπx) (其中m=1,2,3…)

(23)

将式(24)代入式(20)可得

λ2=P-Γ=P-3c2λ2

(24)

可知边界条件中常数c和载荷P有关。

3 数值算例

由图2可知：(1)随着轴向载荷的逐渐加大，壁板在P=π2处发生了突变，平衡点也由原来的一个(x=0)变成了3个。(2)当轴向载荷P大于第一阶临界屈曲载荷时，即P>π2时，在x=0处的平衡点变为不稳定平衡点，且壁板在临界值P=π2处出现分岔，壁板发生屈曲。轴向载荷越大，壁板偏离平衡位置越远。(3)当轴向载荷继续增大，超过第二阶临界屈曲载荷时，即P>4π2时，壁板存在三种平衡：第一种是不稳定的静平衡构型；第二种是步骤(2)中的屈曲构型；第三种是新产生的屈曲构型，屈曲构型如图2所示。(4)当轴向载荷继续大于第三阶临界屈曲载荷，即P>9π2时，壁板存在三个非平凡解，相应的对应如图2所示三个屈曲构型。

图2 二维壁板在x=0.25处前三阶弯曲构型静态分岔图

通过以上的静态分岔图分析可以得知，温度对壁板的稳定性有着很重要的影响，热应力越大，系统的构型就越复杂。由(14)式可知，对于选定的系统模型，温差ΔT是影响热应力的重要因素，故本文再次通过算例研究了不同温差ΔT下壁板偏离平衡位置的程度。图3描绘了三种不同温差(ΔT=1、ΔT=3、ΔT=5)下，壁板系统偏离平衡位置的情况。

图3 不同温差下二维壁板的弯曲构型

由图可知，当温差ΔT不同时，壁板在同一位置偏离平衡位置的程度也不同，温差T越大，壁板偏离平衡位置就越远。由此可知，温差的大小对壁板的弯曲构型有很大的影响。

4 结论

本文运用Von Karman大变形非线性应变-位移关系，基于Kirchhoff平板理论，建立了热环境下二维壁板在超音速流作用下的颤振微分方程，分析了温度变化对壁板颤振的影响规律，可得出如下结论：

(1)热应力是降低壁板稳定性的一个因素。随着热应力的增大，壁板系统的轴向载荷大于临界载荷时，壁板偏离平衡位置，并发生屈曲。热应力继续增大时，壁板系统同时存在多种平衡位置，对应着多种屈曲构型。

(2)温差T是影响热应力的一个重要因素。当温差越大时，壁板同一位置偏离平衡点的位移也越大，温差的存在使得壁板表现出的热颤振特性更加复杂。

[1]杨智春，夏巍，孙浩.高速飞行器壁板颤振的分析模型和分析方法[J].应用力学学报，2006，23(4):537-542.

[2]Houbolt J C.A study of several aerothermoelastic problems of aircraft in high-speed flight[D].Eidenossischen Technischen Hochschule,The Swiss Federal Institute of Technology,Zurich Switzerland,1958.

[3]Yang T Y,Han A D.Flutter of thermally buckled finite element panels[J].AIAA Journal,1976,14(7):975-977.

[4]Xue D Y,Mei C.Finite element non-linear panel-flutter with arbitrary temperature in supersonic flow[J].AIAA Journal,1933,31(1):154-162.

[5]Xue D Y,Mei C.Finite element nonlinear flutter and fatigue life of two dimensional panels with temperature effects[J].Journal of Aircraft,1993,30(6):993-1000.

[6]Ghoman S,Mei C,Azzouz MS.Frequency domain method for flutter analysis of curved panels under yawed supersonic flow at elevated temperature[R].AIAA,2008-2312,2008.

[7]Ghoman S,Mei C,Azzouz MS.Time domain method for nonlinear flutter of curved panels under yawed supersonic flow at elevated temperature[R].AIAA,2009-2598,2009.

[8]张蕊丽，杨智春.曲壁板在超音速气流中的分岔特性[J].力学学报，2010,42(5):863-869

[9]杨智春，周建，谷迎松.超音速气流中受热曲壁板的非线性颤振特性[J].力学学报,2012,44(1):30-38.

[10]陈文俊.气动加热对飞行器气动弹性特性的影响[J].现代防御技术，1998,26(3):20-28.

[11]Chu H N,Herrmann G.Influence of large amplitudes on free flexural vibration of rectangular elastic plates[J].Journal of Applied Mechanics,1956,23(10):532-540.

[12]Nayfeh A H,Emam S A.Exact solutions and stability of the postbuckling configurations of beams[J].Nonlinear Dynamics,2008,54(4):395-408.

[13]Ashley H,Zartarian G.Piston theory-A new aerodynamic tool for the aeroelastician[J].Journal of Aeronautical Science,1956,23(10):1109-1118.

(责任编辑：吴萍 英文审校：刘敬钰)

Nonlinearthermalflutterfeaturesofheatedpanelsinsupersonicairflow

WANG Guang-sheng1,YANG Xiao-dong2

1.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136;2.School of Mechanical and Electrical Engineering,Beijing University of Technology,Beijing 100124)

Panel thermal flutter has become the research focus both at home and abroad with the rapid development of high-speed craft technology.Panel thermal flutter has a great influence on vehicle performance,and even affects the flight safety.The nonlinear flutter analysis of panel with thermal effect is carried out.Based on the Kirchhoff thin plate theory and the Von Karman′s nonlinear large deformation strain-displacement relations,the dynamic equations of the flat panel are established.The paper takes the point atx=0.25 as an example to draw its first three curved configuration static bifurcation diagrams,and the buckling configuration of panel of different axial load conditions is analyzed.As the difference in temperature is an important factor affecting the thermal stress,the paper compares the elastic deformation of different temperature conditions,and results show that the greater the temperature difference is,the greater displacement of the panel deviation from the static equilibrium position will be.

general mechanics;thermal flutter;panel flutter;supersonic flow;aerodynamic heating effect

2013-05-28

国家自然科学基金(项目编号：11172010,10702045)

王广胜(1987-)，男，山东泰安人，在读研究生，主要研究方向：非线性动力学与结构振动，E-mail:wzss1987@126.com； 杨晓东(1977-)，男，河北沧州人，教授，主要研究方向：非线性动力学与结构振动，E-mail:jxdyang@163.com。

2095-1248(2014)01-0020-04

O322

A

10.3969/j.issn.2095-1248.2014.01.005