高频超声清洗中声场分布的仿真及实验研究

谢爱云，黄雅婷，冯 涛，董秀萍

(北京工商大学材料与机械工程学院，北京 100048)

高频超声清洗中声场分布的仿真及实验研究

谢爱云，黄雅婷，冯 涛，董秀萍

(北京工商大学材料与机械工程学院，北京 100048)

高频超声乃至兆声清洗广泛应用于半导体器件的超精密清洗，可以有效去除纳米颗粒污染。其中，声能在声场中的分布决定了清洗效果，包括去除均匀性和清洗对象破坏。对于矩形清洗槽内的声场分布，采用简正分解理论直接求解声压分布。结果表明，兆声声能集中于声源辐射轴所在的局部区域，声压波腹和波节分布反映声源振动面形状，而超声波声能扩散至全声场。采用水听器对超声波声场声压分布进行测量，与理论结果相符。由于截断误差和非线性空化误差的存在，理论值小于实验测量结果。

兆声清洗；纳米颗粒；声场；计算机仿真

兆声清洗广泛应用于半导体制造行业。兆声清洗由超声波清洗发展而来，20～800 kHz为超声，800 kHz以上频率的声波称为兆声波[1]。兆声清洗采用兆声清洗槽水浴[2]或兆声喷嘴喷射清洗液[3]，将声波能量通过清洗液传递到物料表面。高频交变声压导致流体振动、空化气泡产生、微气泡振动、边界层减薄等诸多效应[4-5]。在高速流体对表面不断冲击下，表面吸附的颗粒等污染物暴露后被提拉或滚动除去。

随着超大规模集成电路的广泛使用和计算机制造技术的飞速发展，铜和低介电材料的使用和大马士革镶嵌加工工艺已经成为互连加工标准工艺[6]，下一代半导体器件的线宽已达22 nm。铜的化学性质活泼，低介电材料的机械强度低于传统材料，加之小特征尺寸对表面污染和缺陷的容忍度降低，怎样在提高表面质量的同时避免缺陷发生，成为化学机械抛光以及其后清洗工艺中的难题[7-8]。对于兆声清洗声场内能量分布的控制是解决以上2点的重要途径[9]。因此，对声场分布的测量、仿真和预测是有效控制声场的首要问题。水听器常用于声压场的测量[10]，近年来又发展了利用声致发光测量空化效应[11]、荧光颗粒追踪声流[12]等技术。声场计算一般利用有限差分法求解波动方程，但对于计算域和边界条件较为简单的声场，微分方程的求解显得较为繁琐[13]。

简正分解理论和声源镜像原理常用于室内声场计算[14-15]，本文通过对清洗槽边界条件及其内部声波传播特点进行分析和合理简化，建立了简正分解理论适用的声场模型，对超声和兆声清洗槽内声波传播的声压场直接求解，通过计算机仿真，预测声压分布情况，利用水听器测量清洗槽内的声压，实验结果与仿真结果相符合。

1 声场测试

1.1实验设备

实验系统包括信号采集和数据处理2部分。信号采集部分由清洗机、水听器和示波器组成，数据处理由计算机完成。测量系统示意图如图1所示。在超声波清洗机工作过程当中，利用水听器逐点测量清洗液(水)中的声压值，并转换为电信号，由示波器采集后输入计算机进行分析和处理。

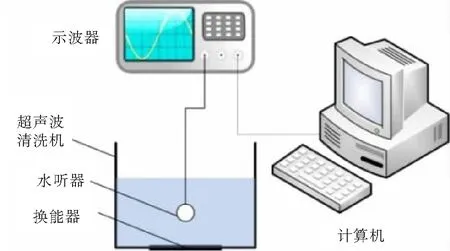
图1 超声波声场测试实验系统示意图Fig.1 Schematic diagram of experimental system for ultrasonic sound field measurement

信号采集部分具体的设备参数如下。

1)BG-01超声波清洗机 超声波清洗机容积为150 mm×140 mm×100 mm，输出频率为40 kHz，功率为80 W，底部有一个圆形换能器，半径约为36 mm，中心位置略偏离底面中心。

2)CS-3型水听器 实验中所选水听器由中国科学院声学研究所研制，测量探头直径为8 mm，传感元件压电陶瓷管，测量频率最高为200 kHz。水听器输出阻抗Xc与被测信号频率有关，

Xc=1/(2πfC)。

(1)

式中：电容C为10～100 pF；超声波频率f为40 kHz。计算出水听器的阻抗量级为105Ω，超声波在水中的波长为37 mm，探头直径小于波长的1/4，可以保证测量精度。

3)泰克TDS2014b数字存储示波器 示波器为美国Tektronix公司产品，最大采样率为1 GSa/s(即1 s采样个数为1 G)，带宽为100 MHz，记录长度为2 500点，时间轴分度为5 ns～50 s。对于40 kHz超声波，采样频率选25 MHz，所选示波器满足采样定理和带宽要求。示波器的阻抗为1 MΩ，大于水听器阻抗一个数量级，满足阻抗匹配。

1.2主要步骤

1)在清洗槽中加入高度为94 mm的水，室温(约20 ℃)，接通电源，待声场稳定后开始测量，测量过程中及时加水使液面高度变化不超过1 mm。

2)对距底面30 mm的平面进行逐点扫描测量，采样点分布为11行、13列，共143个点，行列平行于清洗槽边界，间距10 mm，中心采样点位于底面的垂直中心线上。水听器在各个采样点位置的偏移距离不超过1 mm，摆动幅度不超过0.5 mm。由于水听器尺寸限制，清洗槽边界部分无法测量，实测范围为120 mm×100 mm。

3)水听器的输出端连接示波器显示波形，读取电压信号，通过前面板的USB接口将波形数据转存至计算机并进行数据处理。

4)利用Matlab软件运行数据处理程序，对原始信号进行低通滤波，计算滤波后的信号幅值，绘制该平面内的声压幅值分布图。

1.3数据处理

1.3.1 数字滤波

采用Matlab软件设计数字低通滤波器对原始信号进行滤波处理，只保留超声频率，即40 kHz附近的声压信号。图2所示为典型的采样点的信号处理过程，包括以下几部分。

1)读入数据并绘制时域图和幅频谱图。图2 a)为原始信号时域图，大致包含3个半周期；图2 b)为原始信号的幅频谱图，在40 kHz附近有最大值，同时还存在高频的干扰。

2)设计数字低通椭圆滤波器对原始信号进行滤波。椭圆滤波器在通带和阻带内都具有等波纹振幅特性，在相同阶数下，相比其他滤波器具有最小的通带和阻带波动。技术指标采用通带和阻带截止频率分别为50 kHz和80 kHz，通带最大衰减量为1 dB，阻带最小衰减量为50 dB，采样频率为25 MHz。

3)绘制滤波后的时域图和幅频谱图。图2 c)为滤波后的时域图，为标准正弦波形；图2 d)为滤波后的幅频谱图，经过滤波处理后，高频干扰信号被成功滤除，超声频率的声压信号得到保留。

图2 采样原始波形及数字滤波结果Fig.2 Original waveforms and digital filtered results of the sampling

1.3.2 声压幅值的计算

水听器测得的数据为电压信号，需要转变成声压信号。水听器灵敏度级M0为[16]

M0=20×lg(M2/M1)。

(2)

式中：M1为基准灵敏度；M2为水听器的灵敏度。通过查阅水听器接收灵敏度表可知在40 kHz时，水听器灵敏度级M0=-210 dB，静水中的基准灵敏度取M1=1×106V/Pa。代入已知数据，得到40 kHz下水听器的灵敏度M2=31.6×10-6V/Pa。

根据水听器输出的各采样点电压幅值U，可以计算声压幅值PA，

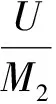
2 声场模型及仿真

2.1声场模型

实验中所用清洗机为单声源清洗机，底板上有一个圆形换能器，清洗槽几何形状如图3所示，底部为S=Lx×Ly的长方形，清洗液深度为Lz。声源振动面是半径为r的圆形，圆心位置为(lx,ly,lz)，静止时振动面与底板处在同一水平面，为便于加工制造，单声源一般位于底面靠近中心位置。

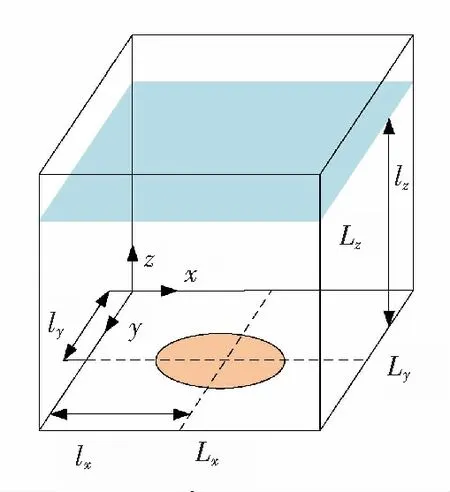
图3 清洗槽模型Fig.3 Cleaning tank Model

2.2驻波简正分解理论

当温度为20 ℃、标准大气压时，钢、水和空气的特性阻抗分别为4.68×107瑞利、1.48×106瑞利和4.15×102瑞利。三者之间差别超过一个数量级，所以清洗槽与水边界简化为刚性边界，空气与水边界简化为自由边界(声压值恒为零)，因此清洗液所占空间构成三维波匣。对于换能器功率较低的情形，不考虑强空化作用，满足线性声学条件。则三维波动方程为

(3)

式中：c为清洗液中的声速；P为声压。为简化计算，考虑x和y方向的反射边界，z向采用镜像法叠加，暂不考虑z向反射波，则x，y方向存在驻波，z方向无限延伸，只存在行波，所以式(3)中各方向的波函数分别为

(4)

系数kx，ky，kz满足：

(5)

式中：波数k=ω/c=2πf/c；f为频率；ω为圆频率。质点振动速度正比于声压梯度，可以解得x，y，z方向上的质点速度：

(6)

其中ρ为介质密度。因为z方向无限延伸，所以x，y为刚性边界条件，即vx|x=0,Lx=0和vy|y=0,Ly=0，可以确定参数

(7)

于是对应于一组整数(n，m)，有(n，m)次简正波，即波动方程的一个特解Pnm：

Pnm=Anmcos(kxx)cos(kyy)ej(ωt-kzz)。

(8)

受实数波的限制，简正波次(n，m)应满足：

(9)

振幅参数Anm可由底面声源振动分布进行求解，可以表示为

Anm=ρωanm/kz,

(10)

其中常系数：

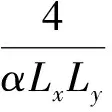
(11)

当n=m=0时，a=4；当n或m仅一个为零时，a=2；当n和m均不为零，a=1。实际声场中的总声压应为各次简正波的线性叠加。再依据镜像原理，对清洗液与空气间自由边界形成的反射波叠加，反射波等效为与实声源关于液面对称位置存在一个虚声源，虚声源与实声源幅值相同，相位相反，可以得到总声压函数：

P= ∑Anmcos(kxx)cos(kyy)(ej(ωt-kzz)-ej(ωt-2kzLz+kzz))=

∑Cnm(ej(ωt-kzz)-ej(ωt-2kzLz+kzz)。

(12)

通过波矢的矢量求和，容易计算出实际声压幅值PA为

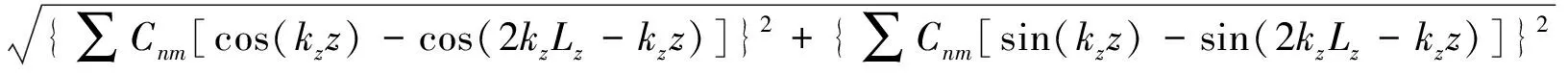
(13)

3 结果与讨论

单声源声场中距底面30 mm处声压分布如图4所示，视图方向为x-y面，x轴方向刻度范围15～135 mm，y轴方向刻度范围20～120 mm。数值计算采用Matlab软件平台自行编写求解程序。图4 a)为超声波(40 kHz)声场理论计算结果，PA/P0为无量纲的声压幅值；图4 b)为超声波(40 kHz)实验测量结果，U为示波器输出的电压波形的振幅，单位为V；图4 c)为兆声波(1 MHz)声场理论计算结果。

图4 距底面30 mm的水平面声压幅值分布图Fig.4 Sound pressure amplitude distribution on the horizontal plane 30 mm above the bottom

3.1单声源超声波声场

理论计算采用与实验设备相同的参数，清洗槽的长度Lx=150 mm，宽度Ly=140 mm，液面高度Lz=94 mm。底面声源振动面中心位置坐标为(75 mm，55 mm)，半径r=36 mm，超声波频率f=40 kHz，圆频率ω=2.5×105s-1。忽略水中气泡的影响，水中的声速可以认为与纯水中的声速相等，取c=1.48×103m/s，则输出超声波的波数k=ω/c=1.69×102m-1，波长λ=c/f=37 mm，水的密度ρ=1.0×103kg/m3。计算中采用无量纲的单位，速度单位取为换能器振动面的速度幅值v0，压强取P0=ρcv0。

从声场当中的声压幅值分布看，声波能量分散在整个平面内，声压最大值出现在换能器圆平面的中心轴线上，波腹与波节交替出现，围绕换能器所在圆平面的中心轴呈矩形环状分布。

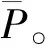
(14)

(15)

3.2单声源兆声波声场

由前述分析，简正分解理论更适用于兆声波声场。改变频率输入值，f=1 MHz，其他参数与计算单声源超声声场时的参数相同。由距底面30 mm的水平面的兆声波声场分布可知，声场中声源辐射面(半径36 mm)对应的半径38 mm左右的圆形区域内，声压幅值明显高于其他区域，表明此区域集中了绝大部分的声能。这主要由于兆声波的波长很短，声波指向性高，能量集中于换能器中心轴线。声源振动面中心为波腹，以声源中心为圆心向外，声压波腹和波节呈圆环状交替出现，相邻波腹间的距离约为10 mm，声源振动面边界处声压迅速减小。超声场的波腹波节变化情况为矩形环状分布，反映了清洗槽形状特征，而兆声场的圆形环状分布则反映了换能器的形状，与清洗槽形状无关。因此对于兆声波清洗来说，声场优化针对声源设计进行即可。此外，兆声波的波腹波节较密集，在清洗时应注意采用样品小幅振动等方式，保证样品表面的声场均匀。

4 结 论

针对典型的超声波清洗设备，给出了采用驻波的简正分解理论计算声场分布的方法，给出频率40 kHz底面单声源声场的数值计算结果。利用水听器对40 kHz超声波声场的实验测量验证理论结果，并给出1 MHz频率的底面单声源兆声波声场理论计算结果。

频率40 kHz的超声波，声波能量向辐射面以外的区域扩散，声波能量分散在整个平面上，声压最大值出现在换能器中心轴上，波腹和波节交替出现，围绕换能器中心轴呈矩形环状分布。实验测量结果与理论计算结果相符。由于截断误差和非线性空化误差的存在，所以理论值小于实验测量结果。

频率1 MHz的兆声波频率，声波的指向性很高，声波能量集中在声源辐射面内，声源振动面中心为波腹，以声源中心为圆心向外，声压波腹和波节呈圆环状交替出现，反映声源振动面形状，声源振动面边界处声压迅速减小，辐射面以外的区域几乎无声能分布。

/

[1] 雷 红. CMP后清洗技术的研究进展[J].半导体技术，2008,33(5):369-373. LEI Hong. Advances in post-CMP cleaning technology[J]. Semiconductor Technology, 2008,33(5)：369-373.

[2] 刘玉岭，李薇薇，檀柏梅. 微电子工艺中的清洗技术现况与展望[J].河北工业大学学报，2002,31(6):11-17. LIU Yuling, LI Weiwei, TAN Baimei. Present situations and prospects of cleaning technology in microelectronics[J]. Journal of Hebei University of Technology,2002,31(6):11-17.

[3] HYUNSE K, YANGLAE L, EUISU L. Development of a single-beam megasonic system for nano-particle cleaning[J]. The Electrochemical Society, 2009, 25 (5): 281-286.

[4] GLENN W G, BUSNAINA A A. Roles of cavitation and acoustic streaming in megasonic cleaning[J]. Particulate Science and Technology,1999(17):229-238.

[5] HABUKA H, FUKUMOTO R, OKADA Y, et al. Dominant forces for driving bubbles in a wet cleaning bath using megasonic wave[J]. Journal of Electrochemical Society, 2010, 157(6)：585-588.

[6] 唐心亮, 智兆华, 刘玉岭，等. ULSI碱性抛光液对铜布线平坦化的影响研究[J]. 河北科技大学学报，2011,32(4)：380-383. TANG Xinliang, ZHI Zhaohua, LIU Yuling, et al. Study on effect of alkaline slurry on copper planarization in ULSI[J]. Journal of Hebei University of Science and Technology，2011,32(4)：380-383.

[7] XUN G, TAKENAO N, AKINOBU T, et al. Tribological study of brush scrubbing in post-chemical mechanical planarization cleaning in non-porous ultralow-k dielectric/Cu interconnects[J]. Journal of Electrochemical Society, 2011, 158(11):1145-1151.

[8] PACCO A,HALDER S,KENIS K, et al. Cleaning and damage performance of single wafer cleaning tools using physical removal forces[J].The Electrochemical Society, 2009, 25(5):311-317.

[9] 刘永进,杜建科,冯小强. 单晶圆兆声清洗技术研究及兆声喷头方案优化[J].电子工业专用设备, 2011(1):15-17. LIU Yongjin，DU Jianke，FENG Xiaoqiang. Study of single-wafer megasonic cleaning and optimization of megasonic nozzle[J]. Equipment for Electronic Products Manufacturing, 2011(1):15-17.

[10] KOCH C, JENDERKA K V. Measurement of sound field in cavitating media by an optical fibre-tip hydrophone[J]. Ultrasonics Sonochemistry, 2008(15):502-509.

[11] HAUPTMANN M , STRUYF H, MERTENS P .Towards an understanding and control of cavitation activity in 1 MHz ultrasound fields[J]. Ultrasonics Sonochemistry, 2013，20:77-88.

[12] KIM W, KIM T H, CHOI J, et al. Mechanism of particle removal by megasonic waves[J]. Appled Physics Letters, 2009,94(8)：1908-1910.

[13] 黄志刚.基于数值仿真的流体振动抛光机理研究[D]. 广州：广东工业大学，2007. HUANG Zhigang, Research of the Machining Mechanisms of Polishing Based on Vibrations of Liquid with Numerical Simulations[D]. Guangzhou：Guangdong University of Technology，2007.

[14] 杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社，2001. DU Gonghuan, ZHU Zhemin, GONG Xiufen. Fundamentals of Acoustics[M]. Nanjing: Nanjing University Press, 2001.

[15] LEHMANN E A, JOHANSSON A M. Prediction of energy decay in room impulse responses simulated with an image-source model[J]. Acoustical Society of American, 2008,124(1):269-277.

[16] 陈克安，曾向阳，李海英.声学测量[M].北京：科学出版社，2005. CHEN Kean, ZENG Xiangyang, LI Haiying. Acoustic Measurement[M].Beijing: Science Press, 2005.

Simulation and experiments research of acoustic field distribution in high frequency ultrasonic cleaning

XIE Aiyun, HUANG Yating, FENG Tao, DONG Xiuping

(School of Materials and Mechanical Engineering, Beijing Technology and Business University, Beijing 100048, China)

High frequency ultrasonic, even megasonic bath cleaning has been one of the most successful techniques for nano-particle removal in semiconductor manufactural. The megasonic energy in sound field determines the cleaning effect, including the uniformity removal and object destruction cleaning. The distribution of sonic pressure in a wet cleaning bath is simulated based on normal mode decomposition theorem. The results show that megasonic wave can focus on the local area of sound radiation zone axis, and the distribution of wave nodes reflects the shape of vibration source, which is different from low frequency ultrasonic with diffuse sound energy. The measurement of ultrasonic sound pressure hydrophone is consistent with the theoretical results. The theory value is lower than the experiment value due to the cut-off error and nonlinear cavitation effect.

megasonic cleaning； nano-particle； acoustic field； computer simulation

2014-03-14；

2014-04-18；责任编辑：张士莹

国家自然科学基金(51205006)

谢爱云(1989-)，男，湖北荆州人，硕士研究生，主要从事半导体制造及摩擦学方面的研究。

黄雅婷博士。E-mail:huangyating@th.btbu.edu.cn

1008-1542(2014)04-0324-06

10.7535/hbkd.2014yx04003

TN305

A

谢爱云，黄雅婷，冯 涛，等.高频超声清洗中声场分布的仿真及实验研究[J].河北科技大学学报,2014,35(4):324-329.

XIE Aiyun, HUANG Yating, FENG Tao,et al.Simulation and experiments research of acoustic field distribution in high frequency ultrasonic cleaning[J].Journal of Hebei University of Science and Technology,2014,35(4):324-329.