小提琴共鸣箱振动特性的有限元仿真与实验研究

张承忠， 叶邦彦， 曹云凤， 梁立东， 赵学智

(1.华南师范大学软件学院，佛山 528225；2.华南理工大学机械与汽车工程学院，广州 510640)

小提琴音色优美，音域宽广，既是艺术界的乐器王后，又属于科技界的精密声学设备[1-2]. 一直以来，人们通过各种科学方法和实验，寻求制作优秀提琴的规律[3]. 作为小提琴的主要部分，共鸣箱承受来自琴弦和琴码的张力和压力，并经过充分振动才能发出好的声音，其影响因素较多，机理复杂. 德国科学家Cremer的专著介绍了小提琴的物理原理以及研究的各种实验方法[4]. 文献[5]、[6]研究小提琴面板、背板在不同尺寸及形状下的振动情形，以及小提琴共鸣箱内部空气的振动现象. Gough[7]用有限元方法分析小提琴的结构模式及小提琴共鸣箱体的几个主要结构参数的变化对箱体振动的影响. 美国科学家Hutchins和哈佛大学的物理学家Frederick合作研究了小提琴琴板的声学特性[8]. 国内学者研究了提琴自由琴板振型以及音柱对振型影响[9].

本文针对以往小提琴共鸣箱有限元仿真存在的问题，着重提高模型的真实性和精确度，将琴码和共鸣箱作为一个整体进行研究. 提琴共鸣箱几何形状复杂，有限元法是对这种复杂结构进行数值计算分析的首选[10-11]. 本研究首先根据小提琴共鸣箱实体创建CAD模型，包括面板、背板、侧板、腔内结构和辅助组件，然后对小提琴琴板和琴体进行有限元仿真，研究其模态及频响，为了验证有限元分析的结果，采用振动传感器测量拉弦和拨弦时面板、背板的振动情况，验证共鸣箱的频率响应特性. 以进一步弄清小提琴共鸣箱耦合共振的关键问题.

1 建模方法

1.1 提琴共鸣箱的有限元模型

小提琴共鸣箱的面板和背板为三维曲面，形状复杂，面板上还有F孔和低音梁. 制琴师制作时不仅要做出它们的轮廓，还要求面板和背板的谐振特性适当配合才能得到好的声音效果. 为了能够准确地进行有限元模拟，首先采用“切割法” 由三维建模软件Solidworks创建共鸣箱的有限元模型. 小提琴面板和背板的等高线和厚度分布如图1所示. 根据图中尺寸、厚度分布和等高线进行多截面放样，得到面板、背板和侧板等部件的三维模型.

提琴的低音梁和音柱对提琴发音影响很大，而且结构比较特殊(图2A).采用板-梁复合结构建立模型. 网格划分采用自由网格，并满足声学计算中最高分析频率(4 000 Hz)对应波长至少包括6个结构单元的要求. 图2B显示了包括小提琴琴码的共鸣箱系统结构和网格.

图1 面板和背板的等高线和厚度分布

Figure 1 Contour and thickness distribution of front plate and back plate of violin

图2 小提琴共鸣箱模型的结构与网格划分

1.2 共鸣箱材料特性

提琴的面板、低音梁和音柱用云杉制作；背板、侧板、琴头等用枫木制成. 在有限元分析中，材料属性是否正确对仿真结果有直接影响. 本研究与常规机械构件的有限元模拟不同，考虑木材的各向异性. 木材的力学性能，包括密度和弹性模量等都必须符合提琴的实际材料特性[12]，如表1所示. 并将其弹性模量、剪切模量和泊松系数分解为沿纵、横和垂直3个方向的分量.

表1应用于仿真中的小提琴共鸣箱的材料属性

Table 1 Material properties of violin components using in finite element method

材料参数枫木云杉密度/(kg·m-3)540410杨氏模量Ex/MPa12 4307 590杨氏模量Ey/MPa833592杨氏模量Ez/MPa1 740326.4切变模量Gxy/MPa920463切变模量Gyz/MPa311486切变模量Gxz/MPa1 10622.8泊松比μxy 0.509 0.245泊松比μyz0.3540.372泊松比μxz0.4340.467

2 小提琴共鸣箱的有限元仿真

2.1 共鸣箱的振动载荷与模态分析

小提琴共鸣箱的有限元分析除考虑外力的作用外，还须考虑共鸣箱面板的预应力状态. 仿真时，首先是分析其静态结构，其载荷矩阵为：

[K]{x}={F}.

(1)

考虑面板预应力状态的模态方程为：

式中[K]为刚度矩阵，[M]为质量矩阵，[S]为应力刚度矩阵，ωi为振动频率，φi为模态.

通过受力分析确定边界条件(图3). 其中A、B点分别为弦枕和尾枕端点，C点为琴码顶端. 琴弦的张力F分别作用在A、B处，在C点处存在对琴码的竖直向下的压力T.

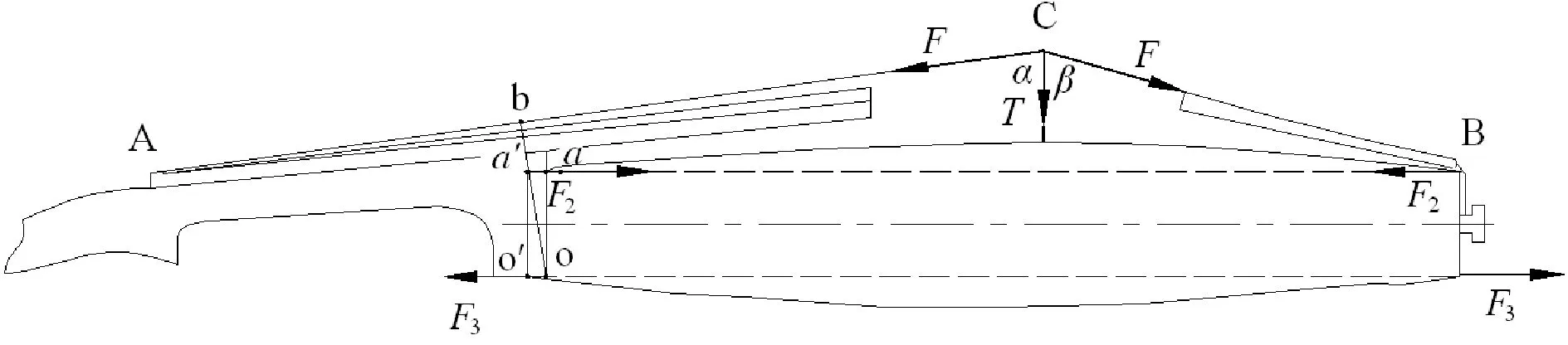
图3 小提琴受力分析

小提琴上弦后，F2为面板上端的纵向压力，F3为背板端部的纵向压力. 假设Mo(F)为弦枕所受力对点o力矩的矢量和，由静态力矩平衡方程则可求出F2和F3.

小提琴的低音梁和音柱对提琴发音影响很大，由于音柱的作用，共鸣箱的发音与音箱不同，面板的振动主要由音柱传递，因此可以忽略空气的作用，但要考虑F孔的结构，它主要通过影响面板的形状和强度起作用. 仿真时选取标准参数的面、背板组成共鸣箱(取表3的6号面板)进行材料参数设置、网格划分，根据图3的受力分析，添加静载荷及约束， 包括琴码脚与面板的接触刚度等，再运用静态结构求解模块来定义分析类型、分析选项、确定载荷数据和载荷步骤选项，然后运用求解器进行求解，得到小提琴共鸣箱静态力作用下的变形情况. 在静态结构分析的基础上，对小提琴共鸣箱进行模态分析，求解出小提琴腔体的振动模态和固有频率(图4).

图4 小提琴共鸣箱的振动模态和固有频率

从图4中的振动模态可分辨面板和背板的振动情况. 两板颜色相同表明振动具有相同的位移方向；出现蓝色和红色意味着相位不同. 当小提琴一对琴板由侧板组成共鸣箱时，由此产生的边缘约束会改变板的振动模态. 此外，两琴板之间通过音柱和侧板的相互作用也会产生新的耦合共振.

表2显示了该标准共鸣箱的5个仿真计算固有频率与文献[13]-[15]中仿真值及实验测量值的比较，结果基本一致. 差异来自测量误差和提琴建模形状、材料力学性能等的不同. 说明木材结构与特性决定的固有模态对小提琴音质的影响很重要. 但文献[13]对共鸣箱进行模态分析时只考虑面板、背板和侧板组成的腔体，忽略了琴码等接触位置的作用力对共鸣箱模态的影响. 本文在提琴受力分析基础上精确设置约束条件，得到的结果更符合提琴的真实情况.

表2琴体共鸣箱固有频率数值计算和实验测量结果的比较

Table 2 Natural frequencies comparison of calculated values and experimental measurements of violin box

模态仿真计算频率/Hz测量频率/Hz仿真值文献值[13]文献值[14]文献值[15]#1427.20410.5432.56410.5#2476.38470.8464.66466.1#3582.46570.2559.59574.1#4706.04730.6……#5761.14767.9…656.1

2.2 共鸣箱结构参数的影响

当小提琴面板和背板的固有频率满足某些特征关系才能制作好的乐器[8]. 但当一对琴板组装成小提琴共鸣箱时，振动系统变得极为复杂. 为了进一步研究影响共鸣箱振动的因素，本文采用不同的面板结构参数(表3)组成共鸣箱，对其振动特性进行研究.

表3 小提琴面板的结构参数Table 3 Structure parameter of violin front plate

首先，研究音柱对提琴共鸣箱振动模态的影响. 文献[8]、[13]仅考虑音柱的位置和音柱粗细对固有频率的影响，除此之外，本文还考虑无音柱的状态和音柱的不同接触刚度对共鸣箱固有频率的影响. 仿真时选取标准厚度2号面板构成的共鸣箱，比较无音柱和不同接触刚度有音柱条件下共鸣箱的振动情况(表4). 仿真结果表明，音柱的不同接触刚度对共鸣箱的模态形状的影响显著，无音柱时对低音影响很大，高音变化相对较小. 音柱与面板的接触刚度(即音柱的松紧)对低频影响较小，当音柱接触刚度增大到一定值时，共鸣箱的高阶共振频率趋向稳定值. 这一结论为提琴音柱状态调整提供了参考.

表4音柱不同接触刚度时共鸣箱共振频率

Table 4 Natural frequencies of violin box with various contact stiffness of sound-post

音柱接触刚度/(N·mm-3)共振频率/Hz#1#2#3#4…#8#9无音柱65191329580…7731 1640.01430497579683…8611 2800.1472583667806…9671 3671.0482585667806…9681 419104825936 687808…9701 419

其次，研究低音梁对共鸣箱的影响. 低音梁的作用除加强面板刚度外，还使面板具有一定的预应力，并将琴码的振动传到整个面板. 选取2号面板构成的共鸣箱. 取标准低音梁高为14 mm，面板预应力是由面板中部向上的加载力使面板产生3 mm挠度变形时形成的. 模拟结果如表5所示.低音梁高度较大和面板有预应力时，共鸣箱的固有频率较高. 因此可通过调整低音梁的尺寸和面板预应力来调整共鸣箱的固有频率.

表5不同低音梁和预应力状态的共鸣箱共振频率

Table 5 Natural frequencies of violin box with various bass bar size and front plate pre-stress state of violin

低音梁状态共振频率/Hz#1#2#3#4…#8#9无低音梁375582653745…885944低音梁(7 mm)378583659777…916953标准低音梁388585667781…933968低音梁有应力431633730840…9691 024

然后，选取表3中面板号1、2、6、7四种不同拱高面板分别与相同的侧板和背板组成共鸣箱，得到的固有频率如表6所示.面板的拱高对共鸣箱的振动影响大，1号平板面板构成的共鸣箱其共振频率较低，与6号面板相比，拱高较低的2号面板低频的共振频率较低，但高频共振频率稍高. 6号面板与7号高拱面板比较，低频的共振频率较接近，但高频相差比较大. 这结论与实际效果相符：当面板的拱高适中时，G弦不会太沉闷，传远性较好，而高频又不太尖噪.

表6不同拱高面板的共鸣箱共振频率

Table 6 Natural frequencies of violin box with various arch rise of front plate

面板号共振频率/Hz#1#2#3#4#5#8#9#1010.0011.1347292…1462162492388585667781806…8569339686427582647706761…7858729147397624681821883…9099831 027

表7为不同厚度面板的共鸣箱的共振频率，是选取2、3、4三种面板组成共鸣箱的结果. 面板厚度适中其共振频率范围较宽；面板太厚时共振频率偏高，这与实际情况相符.

表7不同厚度面板的共鸣箱共振频率

Table 7 Natural frequencies of violin box with various front plate thickness

面板号共振频率/Hz#1#2#3#4#5#8#9#104391486535597651…7578789032388482585667781…8569339683487622757826914…1 0361 1101 141

由表3中2和5两种相同拱高但弧度形状不同的面板得到不同拱弧度形状面板共鸣箱的共振频率(表8).面板拱的形状不同时，共鸣箱的共振频率差别不大，但是中间平两边弧度陡的面板构成的共鸣箱其共振频率略高.

表8不同拱弧度形状面板的共鸣箱共振频率

Table 8 Natural frequencies of violin box with different arch shape of front plate

面板号共振频率/Hz#1#2#3#4#5#8#9#102388482585667781…8569339685398513618698788…8961 0071 060

2.3 共鸣箱的频率响应分析

通过workebench的谐响应模块对小提琴共鸣箱的频率响应特性进行研究. 为了与振动实验测量的频率响应相比较，取频率响应的范围为0～2 500 Hz，模拟时必须根据提琴的受力情况设置合适约束(图5). 其中音柱两端的弹性接触刚度取EFS1=1 N/mm3，驱动力为1.732 N正弦力作用在琴码G弦处，频率在分析范围内变化.

图5 共鸣箱频率响应分析的弹性支承和驱动力配置

Figure 5 The elastic supports and driving force used for analysis of violin box vibration frequency responses

共鸣箱面板和背板的频率响应仿真如图6所示. 面板的共振峰在响应范围的分布比较均匀，背板共振峰则较多分布在高频段. 其频率响应与后面共鸣箱测振实验时相应位置的频率响应结果很接近. 小提琴面板和背板频率响应的不同是因为面板、背板的材料和形状结构不同，同时音柱的作用使面、背板的振动机理不同产生的，较小程度上受粘在面板上的低音梁的影响.

图6 小提琴共鸣箱模拟的频率响应

3 共鸣箱振动测试实验

3.1 共鸣箱振动测试系统设计

小提琴共鸣箱振动测试系统由加速度传感器、电荷放大器和数据采集仪及计算机组成(图7)，加速度传感器检测到的小提琴面板和背板的振动信号经放大与采样后通过计算机处理和显示，并可保存为数据文件以便后续使用. 实验中使用的压电式加速度传感器YD-8的特性为：频响30 000 Hz，质量3 g. 由质量引起的误差可通过补偿算法排除.

图7 小提琴共鸣箱振动测试系统

3.2 滑弦频率响应分析

小提琴共鸣箱频率响应测试的关键是选择合适的激振方法. 由于提琴的结构和使用特点，通常的锤击法不适宜. 根据琴弦亥姆霍兹运动可知，弦振动波形是不对称的锯齿波[5]，逆程变化很陡，含有丰富的高次谐波，因此本文采用滑弦激振，实验时，4根琴弦调整到标准音高，数据采样频率为6 000 Hz，加速度传感器的安装位置，面板安装在琴码之前，距离码脚边线4.5 mm处. 背板则安装在琴马下的中心位置.

图8为G弦滑奏时面板和背板的频率响应，符合前述共鸣箱的频率响应仿真分析结果. A1腔体模态频率在500 Hz附近，它对小提琴音质的影响较大[15]. 有研究表明，优质小提琴在500～600 Hz之间存在一个共振峰[16].

图8 滑奏G弦时频率响应

4 结论

本文通过有限元仿真和实验方法研究了小提琴共鸣箱的振动特性，得到如下结论：

(1)根据有限元仿真对象的特点，将提琴琴码和共鸣箱作为一个系统进行研究，考虑了材料的各向异性、面板预应力状态、码脚和音柱与共鸣箱的接触刚度以及驱动力的形式等，采用板-梁复合结构，建立提琴精确的有限元仿真模型，为了验证有限元分析的结果. 创新性采用滑弦拉奏激励，振动传感器检测的方法，使有限元模拟结果更符合提琴的真实情况.

(2)通过有限元仿真和实验，分析了小提琴面板拱高、拱的形状、板厚和面板预应力、音梁尺寸和音柱接触刚度等结构参数对共鸣箱振动状态的影响，和小提琴共鸣箱结构参数与固有频率和频响的对应关系，明确了以往不清楚的背板在提琴振动谐响峰所起的作用. 使提琴制作时能根据需要，综合考虑各因数的影响，避免了重复实验和盲目性.

参考文献：

[1] Cho A. Probing the secrets of the finest fiddles[J]. Science,2010,328(1): 1468-1470.

[2] Auer L. Violin master works and their interpretation[M]. New York: Dover Publications, 2012.

[3] Heron-Allen E. Violin-making: A Historical and Practical Guide[M]. New York: Courier Dover Publications, 2013.

[4] Cremer L. The physics of the violin[M]. Cambridge, MA: MIT press, 1984.

[5] Lu Y. Comparison of finite element method and modal analysis of violin top plate[D]. McGill University, 2013.

[6] Bissinger G. Global modeling of the violin radiativity profile[J]. The Journal of the Acoustical Society of America, 2010,127(3): 1791-1791.

[7] Gough C. A finite element approach towards understanding violin structural modes[J]. The Journal of the Acoustical Society of America, 2010, 127(3): 1791-1791.

[8] Hutchins C M. The acoustics of violin plates[J]. Scientific American, 1981, 245(4): 170-186.

[9] 张爱林, 贾瑞清, 李直高, 等. 小提琴自由琴板振型分析系统及音柱对振型影响的实验研究 (上)[J]. 乐器, 2009(3): 16-19.

Zhang A L, Jia R Q, Li Z G. Modal analysis of violin plates and impact of sound post on the modals [J]. Instrument,2009(3): 16-19.

[10] 陈瑛, 吴明珠, 胡新荣. 一种改进的质点-弹簧织物建模与仿真[J]. 华南师范大学学报:自然科学版, 2013, 45(5): 43-46.

Chen Y, Wu M Z, Hu X R. An improved mass-spring cloth model and simulation[J]. Journal of South China Normal University: Natural Science Edition, 2013, 45(5): 43-46.

[11] 王石榴. Steward 动感平台体感仿真数值化算法研究[J]. 华南师范大学学报: 自然科学版, 2013, 45(5): 36-39.

Wang S L. Research of steward motion platform somatosensory simulation numerical algorithm [J]. Journal of South China Normal University: Natural Science Edition, 2013, 45(5): 36-39.

[12] Simpson W, TenWolde A. Wood handbook: Wood as an engineering material[M]. Madison, WI: US Department of Agriculture, 1999.

[13] Bretos J, Santamara C, Moral J A. Vibrational patterns and frequency responses of the free plates and box of a violin obtained by finite element analysis[J]. The Journal of the Acoustical Society of America, 1999, 105(3): 1942-1950.

[14] Pyrkosz M, Van Karsen C. Comparative modal tests of a violin[J]. Experimental Techniques, 2013, 37(4): 47-62.

[15] Marshall K D. Modal analysis of a violin[J]. The Journal of the Acoustical Society of America, 1985, 77(2): 695-709.

[16] Georgas P, Schajer G S. Simultaneous measurement of plate natural frequencies and vibration mode shapes using ESPI[M]. Springer New York: In Imaging Methods for Novel Materials and Challenging Applications, 2013,85-90.