寻找2014高考物理实验题中的线性关系
(1.浙江永嘉县上塘中学,浙江 永嘉 325100;2.北京市第八十中学,北京 100102)
在高中物理实验中,各个物理量的关系错综复杂,有些物理量之间存在着线性关系,有些物理量之间存在着非线性关系.图像法是解决上述问题的一个比较直观的途径,但图像法在解题过程中遇到非线性变化关系时,就只能定性研究而难以定量计算.实际上在处理这样的一些非线性数据或问题时,我们可以采用转化的思想,可以将这种非线性关系转化为线性关系,将曲线变化规律转化为直线变化规律,这样有助于分析问题和定量求解.
线性关系图像能形象直观地表达物理规律,有效地减少偶然误差对实验结果的影响,能更方便地分析实验误差,能获得未经测量或无法直接测量的物理量,在实验探究中有广泛的应用.在实验中探究两个物理量间的关系时,通常先引导学生猜想它们之间可能存在的各种关系,然后由实验中测量的数据作出它们对应的图像.在分析和处理实验数据时,我们经常会研究二个变量之间的数学关系,并且希望两个变量之间满足一种简单直观的函数关系——线性关系.因此,寻求、建立和利用线性关系自然就成为高中物理实验中一项重要任务.本文对如何适当地转化物理量的形式,从而建立起它们之间的线性关系等相关问题进行研讨.
高中物理实验中物理量之间有直接线性关系的并不少见,如“探究小车速度随时间变化的规律”实验中的速度与时间的关系;“探究加速度与物体质量、物体受力的关系”实验中的加速度与力的关系;“用伏安法测一节干电池的电动势和内电阻”实验中的路端电压与电流的关系都是直接的线性关系.物理量之间的非线性关系对实验数据的分析和处理往往带来不便,对实验结论的得出自然会增加难度,因此对物理量之间的关系要实施非线性向线性的转化.实验中利用图像来处理实验数据有着直观、简便的特点,更受高考命题者的青睐.笔者认真对比2014年各地高考实验试题,发现以下几题,既符合新课程的实验能力考查要求,又非常新颖,对大部分的考生来说是一个不小的挑战.笔者认真解答这些试题后总结发现:只有把握住线性关系这个技巧,才能有效突破这类图像处理问题.
1 运动学实验中的线性处理

图1
例1(2014安徽卷) 图1是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹.
(1)以下是实验过程中的一些做法,其中合理的有.
a.安装斜槽轨道,使其末端保持水平
b.每次小球释放的初始位置可以任意选择
c.每次小球应从同一高度由静止释放
d.为描出小球的运动轨迹,描绘的点可以用折线连接
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图2中y-x2图象能说明平抛小球运动轨迹为抛物线的是.
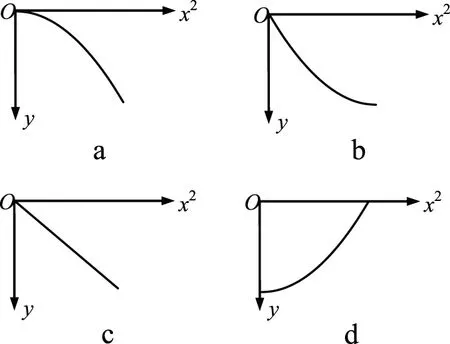
图2
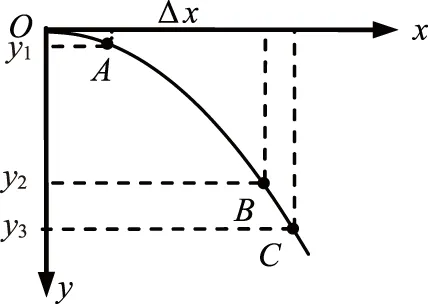
图3
(3)图3是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取三点A、B、C,测得A、B两点竖直坐标y1为5.0cm、y2为45.0cm,A、B两点水平间距Δx为40.0cm.则平抛小球的初速度v0为m/s,若C点的竖直坐标y3为60.0cm,则小球在C点的速度vC为m/s(结果保留两位有效数字,g取10m/s2).
解析:(1)“研究平抛物体运动”的实验斜槽轨道末端保持水平为了保证水平初速度.从同一高度由静止释放为了保证每次的水平初速度相同,a、c正确.


2 力学实验中的线性处理
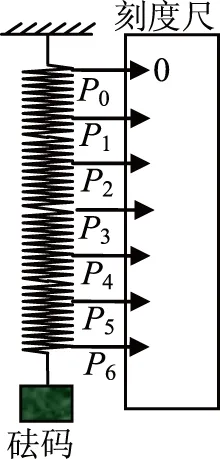
图4
例2(2014新课标全国卷Ⅱ) 某实验小组探究弹簧的劲度系数k与其长度(圈数)的关系,实验装置如图4所示:一均匀长弹簧竖直悬挂,7个指针P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处;通过旁边竖直放置的刻度尺,可以读出指针的位置,P0指向0刻度;设弹簧下端未挂重物时,各指针的位置记为x0;挂有质量为0.100kg砝码时,各指针的位置记为x;测量结果及部分计算结果如下表所示(n为弹簧的圈数,取重力加速度为9.80m/s2).已知实验所用弹簧的总圈数为60,整个弹簧的自由长度为11.88cm.

P1P2P3P4P5P6x0 (cm)2.044.066.068.0510.0312.01x (cm)2.645.267.8110.3012.9315.41n102030405060k(N/m)163①56.043.633.828.81/k(m/N)0.0061②0.01790.02290.02960.0347
(1)将表中数据补充完整:①,②;
(2)以n为横坐标,1/k为纵坐标,在坐标纸上画出1/k~n图像;
(3)图中画出的直线可以近似认为通过原点;若从实验中所用的弹簧截取圈数为n的一段弹簧,该弹簧的劲度系数k与其圈数n的关系的表达式为k=③N/m;该弹簧的劲度系数k与其自由长度l0(单位为m)的表达式为k=④N/m.
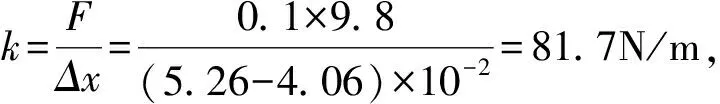
(2)根据表中的数据画出图象,如图5所示.

图5
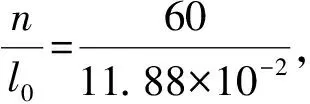
例3(2014新课标全国卷Ⅰ) 某同学利用图6所示实验装置及数字化信息系统获得了小车加速度a与钩码的质量m的对应关系图,如图7所示.实验中小车(含发射器)的质量为200g,实验时选择了不可伸长的轻质细绳和轻定滑轮,小车的加速度由位移传感器及与之相连的计算机得到,回答下列问题:

图6
(1)根据该同学的结果,小车的加速度与钩码的质量成(选填“线性”或“非线性”)关系.
(2)由图7可知,a-m图线不经过原点,可能的原因是.

图7
(3)若利用本实验装置来验证“在小车质量不变的情况下,小车的加速度与作用力成正比”的结论,并直接以钩码所受重力mg作为小车受到的合外力,则实验中应采取的改进措施是,钩码的质量应满足的条件是.
解析:(1)根据图中描出的各点作出的图像是一条曲线而不是一条直线,故小车的加速度和钩码的质量成非线性关系.如果将横坐标质量m改成倒数1/m,则很容易得到加速度a与1/m的线性关系.
(2)根据图7可知:当钩码有一定质量,即细线有一定拉力时,小车加速度仍等于0,说明小车合力等于0,原因是除了拉力外小车还受到摩擦力作用.
(3)实验改进部分有两个要求:第一个就是图像不过原点,需要平衡摩擦力,即要调整轨道倾斜度;第二个就是图像不是直线,因为小车的合力即细线的拉力并不等于钩码的重力,只要满足钩码质量远小于小车质量的条件,就可以得出在小车质量不变的情况下拉力与加速度成正比的结论.
3 电学实验中图像的线性处理

图8
例4(2014四川卷) 图8是测量阻值约几十欧的未知电阻Rx的原理图,图中R0是保护电阻(10Ω),R1是电阻箱(0~99.9Ω),R是滑动变阻器,A1和A2是电流表,E是电源(电动势100V,内阻很小).
在保证安全和满足要求的情况下,使测量范围尽可能大.实验具体步骤如下:
(1)连接好电路,将滑动变阻器R调到最大;
(2)闭合S,从最大值开始调节电阻箱R1,先调R1为适当值,再调滑动变阻器R,使A1示数I1=0.15A,记下此时电阻箱的阻值R1和A2示数I2.
(3)重复步骤(2),再测量6组R1和I2;
(4)将实验测得的7组数据在坐标纸上描点(如图9).
根据实验回答以下问题:
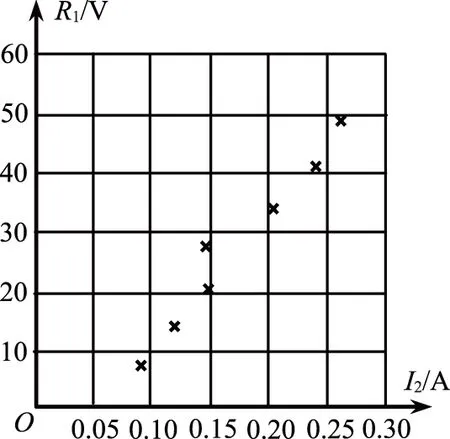
图9
①现有四只供选用的电流表:
A.电流表(0~3mA,内阻为2.0Ω)
B.电流表(0~3mA,内阻未知)
C.电流表(0~0.3A,内阻为5.0Ω
D.电流表(0~0.3A,内阻未知)
A1应选用,A2应选用.
②测得一组R1和I2值后,调整电阻箱R1,使其阻值变小,要使A1示数I1=0.15A,应让滑动变阻器R接入电路的阻值(选填“不变”、“变大”或“变小”).
③在坐标纸上画出R1与I2的关系图.
④根据以上实验得出Rx=Ω.
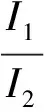
②当R1减小时,如果在滑动变阻器的电阻值保持不变的情况下,电路的总电阻减小,由闭合电路的欧姆定律可得总电流I增大,由分压关系知,并联部分分得的电压减小,则I2减小,由I1=I-I2可知I1将增大.所以当R1减小时,要保持I1=0.15A,则需将滑动变阻器R接入电路的阻值变大.

图10
③根据题目中已知描出的点,平滑连接,删除错误的点,使点分布在图像的两侧(如图10).

以上几道例题,命题者从新颖的角度展示了图像中直线斜率的丰富内涵.不同的试题,赋予了不同的内容,但是如果抓住了图像处理中的线性关系,所有问题都将迎刃而解.笔者认为在平时的实验教学中,不但要注重动手能力的培养,而且也要注意思想方法的渗透,只有这样才能真正提高学生的实验能力.因此在平时的实验复习中,要培养利用图像解决问题的意识,当测量数据成非线性关系时,应洞察两个物理量的变化关系,掌握这类问题的处理策略,从线性关系角度建立合适的坐标,来解决相关的物理问题.
若物理规律中的物理量之间的关系可以转化为最简单的正比关系,则用线性关系图像法处理较为方便、直观.利用线性关系图像处理实验数据时,可剔除那些明显不在直线上的点,以减少偶然误差;用图像法处理数据,因该直线的斜率不变,利用直线的斜率求得的物理量,理论上可消除系统误差.利用线性关系图像的合理外推可以得到实验中测不到的数据,如电源的电动势、电源的短路电流等.

