运动巧分解 “化难”细无声

(江苏省宜兴第一中学，江苏 宜兴 214200)

一般曲线运动是高考试题中常见的一类难题，有关该类问题的求解策略较多，本文拟通过运用“运动的分解”这一常规思想来巧解带电粒子在磁场中一般的曲线运动．

1 方法

带电粒子在磁场中一般的曲线运动可分解成匀速直线运动和匀速圆周运动的合成．即把初速度分解为两个方向，一个匀速直线运动，这个分速度大小必须满足对应的洛伦兹力与所受的恒力的合力等值反向，另一个分速度则就是做匀速圆周运动的速度．此种方法适用于解决带电粒子在复合场中一般的曲线运动，要求带电粒子除洛伦兹力是变力外其它力必须是恒力．

2 应用

例1 在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O点静止释放，小球的运动曲线如图1所示．已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g．求：

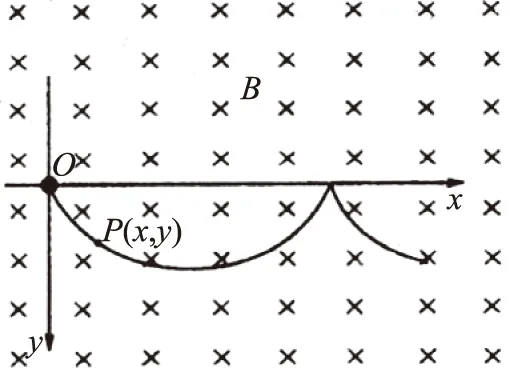
图1

(1)小球运动到任意位置P(x，y)的速率v；

(2)小球在运动过程中第一次下降的最大距离ym；

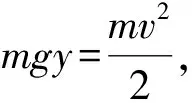
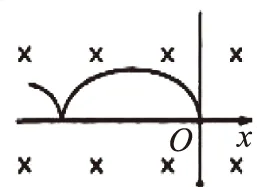
图2

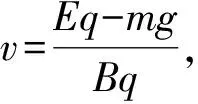
对于初速度不为零的复合场中的运动同样适用，只是两个方向上的速度不是等值反向，而是满足两速度的合速度即为初速度．

例2 如图3所示，在竖直平面内，直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场，左侧到直线距离为d1=0.4m的A处有一个发射枪．发射枪将质量m=0.01kg，带电量q=+0.01C的小球以某一初速度v0水平射出，当竖直位移为d1/2时，小球进入电磁场区域，随后恰能做匀速圆周运动，且圆周最低点C到直线PQ的距离为d2=0.8m．不计空气阻力，g取10m/s2．试求：

图3

(1)小球水平射出的初速度v0和电场强度E；

(2)小球从水平射出至运动到C点的时间t；

(3)若只将PQ右侧的电场强度变为原来的一半，小球进入电磁场区域后做曲线运动，轨迹的最低点为C′，求最低点C′离发射点A的竖直方向距离d及运动过程中的最小速度v．

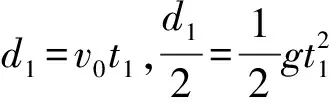
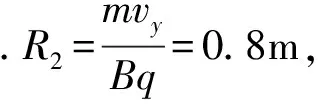
当小球运动至圆周运动的最高点时，速度与匀速向右的速度等值反向，所以它在运动过程中的最小速度为0．

由此可见这种方法不仅适用于初速度为零，同样适用于以任何速度进入磁场中的运动，只要带电粒子进入磁场后除洛伦兹力是变力外，其余力为恒力就可．速度分解的原则也简单易掌握，即一个分速度所产生的洛伦兹力与所受恒力等值反向,另一个分速度则是做匀速圆周运动的速度．所以这种方法不失为解决带电粒子在复合场中一般曲线运动的好方法．