导弹中末制导弹道交接律研究

张 磊,方洋旺,高 翔,刁兴华

(空军工程大学 航空航天工程学院,西安 710038)

复合制导采用不同的导引规律,充分发挥不同制导方式的优点,能够提高中远程导弹的抗干扰能力和制导精度,大大提高了导弹在复杂作战环境下的整体作战效能。复合制导过程一般分为4个阶段:初制导段、中制导段、交接过渡段以及末制导段[1]。其中交接过渡段是导弹从中制导向末制导过渡的中间过程,又被称为中末制导交班。通常情况下中末制导交班主要包括2个方面的含义[2]:一是导引头交班,即导引头必须可靠截获目标;二是弹道交班,即导弹弹道的平滑交接。

在中制导段,针对导引头交班问题,通过合理设计的中制导律,可以使得在末制导启控时弹目之间的连线位于导引头视场范围,满足导引头交班的条件[2]。但由于中远程导弹在中制导和末制导阶段分别采用不同的制导律,因而具有不同的弹道特性,当导弹由中制导转到末制导时,可能会出现过载变化剧烈的情况,导弹的运动状态不一定能够立刻适应末制导的要求,这样会导致弹体的不稳定[3]。因此,研究导弹不同制导律作用下的弹道的平滑交接问题,实现导弹中末制导交班时弹道的平滑过渡具有十分重要的实际意义。文献[4]在中制导段和末制导段之间引入弹道交接过渡段,并提出交接过渡段制导的概念,设计了2种复合制导的弹道交接算法——零基交接和自适应交接制导算法。文献[5]采用正弦函数设计了交接段自适应制导算法并分析了算法的航向误差。在零基交接算法中,交接律使得导弹的加速度过渡到0,然后再由0过渡到末制导加速度,虽然能够实现一阶平滑交接,但实际加速度的减小过程有可能使过渡段瞄准误差进一步增大以致导弹丢失目标,且有可能使交接过程中的需用加速度增大、过渡时间变长。而自适应交接制导算法改进了上述缺点,能够实现一阶平滑交接,但无法实现导弹弹道的二阶平滑交接。

本文基于中末制导交接过渡段制导的思想,给出了导弹弹道的平滑交接的条件,将中制导和末制导两种制导律的加速度作为交接律的变量进行加权,设计了一种新的中末制导弹道交接律。

1 导弹弹道交接规律

导弹弹道的平滑交接主要包括两方面:一是导弹弹道的一阶平滑交接,对应于导弹速度矢量能够平滑过渡,即速度矢量的导数存在且连续;二是导弹弹道的二阶平滑交接,对应于导弹加速度矢量能够平滑过渡,即加速度矢量的导数存在且连续。

在交接过渡段,末段导引头开始工作,而中段导引律也仍可以起作用,用两种导引律的加速度作为变量的连续函数来设计交接律,使得导弹的两种制导律能够平稳交接。设a(t)为交接过渡段交接律作用下的导弹加速度矢量,导弹中制导律和末制导律条件下的弹道加速度矢量分别为a1(t)和a2(t),则满足导弹弹道的平滑交接的条件如下。

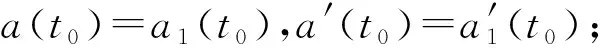
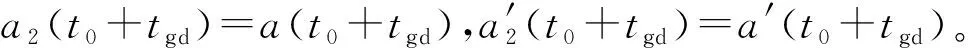
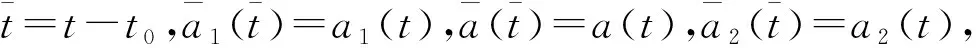
那么,导弹弹道平滑交接的条件就转化为:

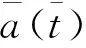
2 平滑算子设计

由平滑交接的条件可知:

则将式(3)分别代入式(1)、式(2),化简得:

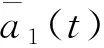
2.1 一次函数平滑算子

假设一次函数交接律如文献[3]的表述形式,即:

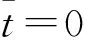
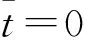
所以,文献[3]所设计的一次函数形式的交接律无法实现二阶平滑交接。

下面,本文提出2种新方法设计交接过渡段制导律,可以同时满足弹道一阶和二阶平滑交接。

2.2 三角函数平滑算子

假设式(1)中的加权系数,即平滑算子为

将式(5)代入式(11)、式(12),可得:

分别求解式(13)、式(14),可得:

将式(15)代入式(11),可得:

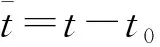
2.3 多项式函数平滑算子

假设式(1)中的加权系数,即平滑算子为

将式(5)代入式(17)、式(18),可得:

分别求解式(19)、式(20),可得:

将式(21)代入式(17),可得:

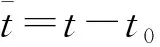
3 仿真实例

下面通过数字仿真来验证所设计的中末制导交接律的性能,在同等情况下将其与采用一次函数形式平滑算子的交接律进行比较,考察不同交接律作用下的导弹加速度的变化情况。

目标的初始位置为(10 000 m,10 000 m),速度300 m/s,速度初始倾角45°,直线运动10 s后以50 m/s2的法向加速度向左转弯,持续时间10 s,再直线运动10 s后以-50 m/s2的法向加速度向右转弯,持续时间10 s,然后作直线运动。导弹中制导开始时刻位于坐标原点,速度为500 m/s,指向目标发射。中制导采用最优制导律,在距目标10 000 m处进行中末制导交接,交接时间为3 s,末制导采用最优滑模制导律。最优制导律和最优滑模制导律[7]分别为

式中:R(t)为弹目相对距离,q为视线角。

仿真结果如图1～图3所示。

图1 直接交接时的仿真结果

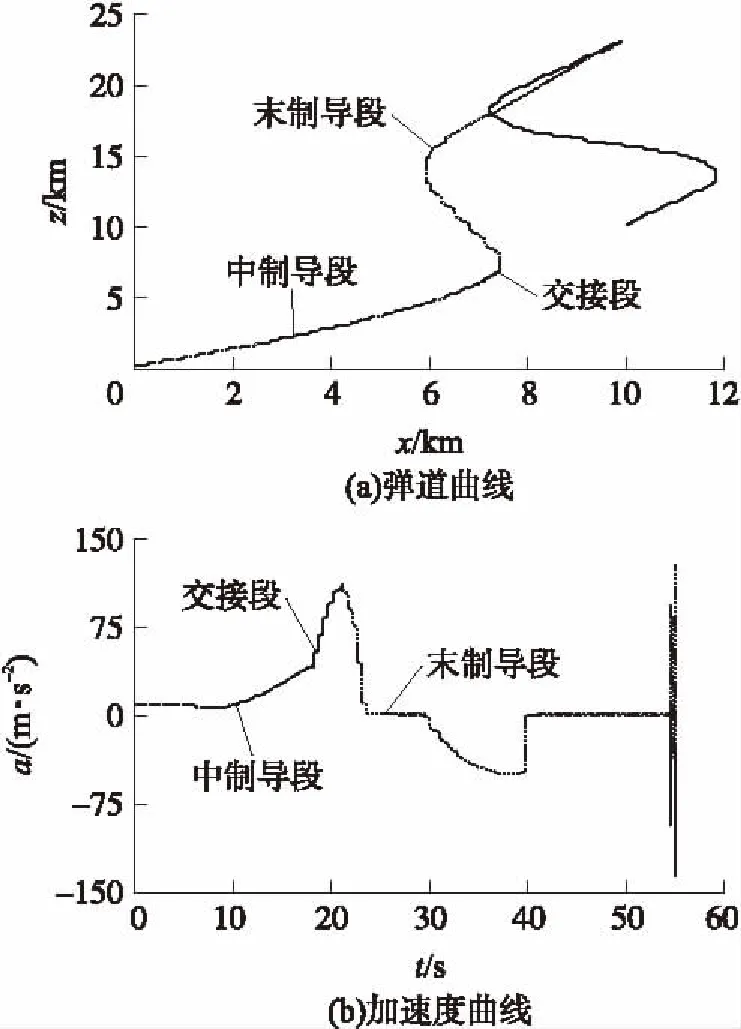
图2 一次函数交接律的仿真结果

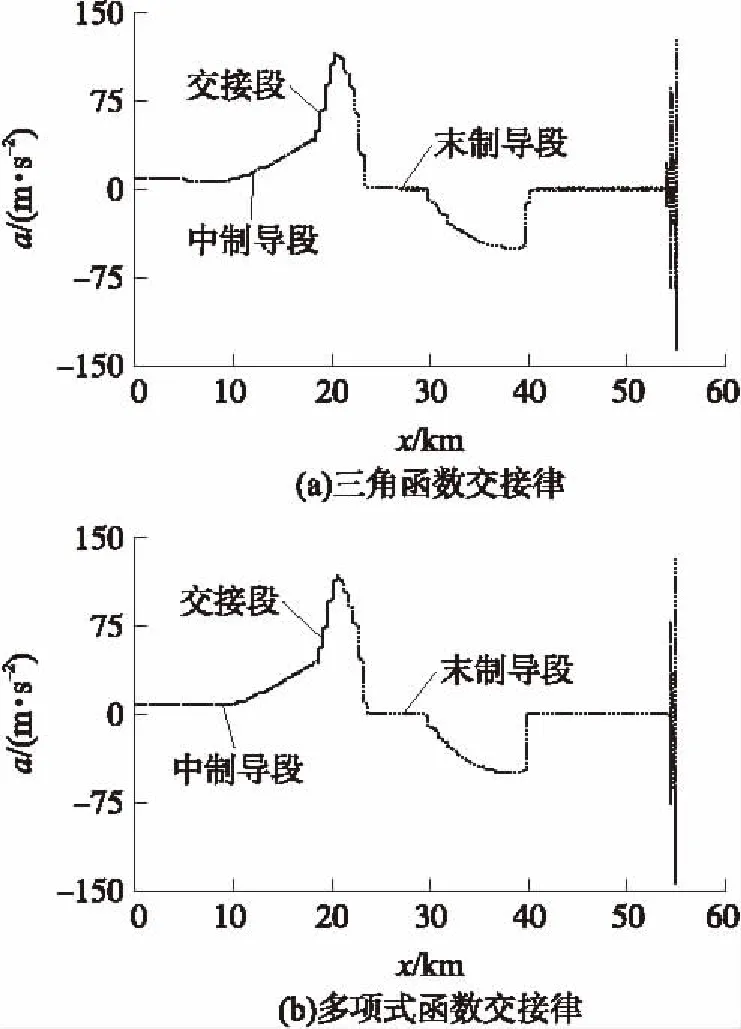
图3 加速度曲线

图1为不采用过渡过程,直接由中制导切换至末制导情形下的仿真结果;图2为采用一次函数形式的交接律的弹道仿真结果,图2(a)、图2(b)分别为各种条件下的弹道曲线和加速度变化曲线;图3中的3(a)、3(b)两图分别为三角函数交接律的加速度变化曲线和多项式函数交接律的加速度变化曲线。由于弹道是慢变量,其变化是十分缓慢和不明显的,仿真中弹道曲线差距不大,因此图未给出弹道曲线。

导弹中末制导弹道交接的目的就是使导弹加速度能够从中制导加速度曲线平滑过渡到末制导曲线上。尽管中末制导分别采用不同的导引规律,通过引入中末制导弹道交接律,能够在确定时间内实现导弹加速度的平滑过渡。对比图2和图3可以看出,采用本文所设计的交接律的加速度曲线更为平滑,不仅能够实现弹道的一阶平滑过渡,而且能够实现二阶平滑过渡;而采用一次函数形式平滑算子的交接律的加速度曲线在t0和t0+tgd时刻的导数不存在(如图2(b)所示),无法实现二阶平滑过渡。

4 结束语

中远程导弹在中末制导交班过程中存在着导引头交班和弹道交班的问题,为了解决中制导段和末制导段间的弹道加速度的平滑过渡问题,本文分别基于三角函数和多项式函数设计弹道平滑过渡算子,实现了中末制导交接段的二阶弹道平滑。与一次函数形式平滑算子的交接律相比,本文设计的中末制导交接律结构明晰,计算简单,具有一定的实际应用价值。

[1] 杨军.导弹控制系统设计原理[M].西安:西北工业大学出版社,1997.

YANG Jun.Design theory of missile control system[M].Xi’an:Northwestern Polytechnical University Press,1997.(in Chinese)

[2] 罗喜霜,张天桥.多用途导弹中末段交班研究[J].弹道学报,2001,13(4):47-50.

LUO Xi-shuang,ZHANG Tian-qiao.Study of handing over between midcourse guidance and terminal guidance for multi-purpose missile[J].Journal of Ballistics,2001,13(4):47-50.(in Chinese)

[3] 王冠军.中远程空空导弹复合制导研究[D].西安:西北工业大学,2004.

WANG Guan-jun.Study on compound guidance of medium and long range missile[D].Xi’an:Northwestern Polytechnical University,2004.(in Chinese)

[4] 侯明善,刘怀勋,张金鹏.中远距战术导弹复合制导的交接规律[J].电光与控制,1998,5(4):14-17.

HOU Ming-shan,LIU Huai-xun,ZHANG Jin-peng.Shifted law of compound guidance of medium and long range tactical missile[J].Electronics Optics and Control,1998,5(4):14-17.(in Chinese)

[5] 王延.近距空空导弹中末制导交接班策略研究[D].西安:西北工业大学,2006.

WANG Yan.Study on handing-off between midcourse and terminal guidance of medium and long range missile[D].Xi’an:Northwestern Polytechnical University,2006.(in Chinese)

[6] 赵占祥.GPS/SINS/MMW复合制导关键技术研究[D].南京:南京理工大学,2006.

ZHAO Zhan-xiang.The research of key techniques of GPS/SINS/MMW compounded controlling and guiding system[D].Nanjing:Nanjing University of Science and Technology,2006.(in Chinese)

[7] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.

ZHOU Di.New guidance laws for homing missile[M].Beijing:National Defense Industry Press,2002.(in Chinese)