步枪弹对复合防护人体上躯干冲击有限元分析

徐 诚,陈 菁,张起宽,康建毅,董 萍,刘 海

(1.南京理工大学 机械工程学院, 南京 210094; 2.第三军医大学 大坪医院野战外科研究所创伤、烧伤与复合伤国家重点实验室,重庆,400042)

枪弹冲击防弹衣后有生目标钝性损伤及其机理研究,既可为提高枪弹威力提供技术途径,又可为个体防护改进和钝性损伤医治提供科学依据,受到了世界各国学者的重视。早期国内外对枪弹冲击防弹衣后的钝性损伤研究主要集中在对带防护的活体动物[1]进行实验,也有采用人尸体进行试验的[2],由于动物与人体相比,解剖尺寸差异较大,且人尸体与人体活体肌张力相差较大,该类研究局限性较大。近年来有限元方法开始应用于防弹衣后有生目标钝性损伤力学机理研究中。Roberts[3]等构建了HSTM假人上躯干有限元模型,进行了手枪弹撞击有软质防护的假人上躯干数值计算,并与模拟假人靶标试验结果进行了对比,证实了该途径的有效性。董萍[4]等也用有限元数值模拟了手枪弹撞击带软质防护的假人上躯干靶标的动态响应。但手枪弹最大撞击速度只有330 m/s,而步枪弹的最大撞击速度可达700～910 m/s,并且软质防弹衣和复合防护衣结构差异较大,目前国内外对高速步枪弹对穿着软硬复合防护衣的人体上躯干的冲击响应了解很少。本文采用有限元方法模拟高速步枪弹撞击有复合防护的人体靶标,分析胸部的冲击响应特征,以期为软硬复合防弹衣后钝性损伤的冲击机理分析、防护结构设计和损伤评估提供依据。

1 有限元模型

1.1 人体上躯干有限元模型

为获得准确的人体三维数据和有限元模型,对一正常成年中国男性进行CT扫描,获取人体上躯干建模源图像;利用医学图像处理软件Mimics进行三维模型重建,获得人体上躯干的三维表面模型,如图 1所示。该模型由“心脏、肺脏、肝脏、胃”等内脏器官、“胸骨、软骨、肋骨、脊柱”等胸廓骨骼、纵膈、皮肤和肌肉组成。基于三维表面模型进行有限元网格划分,将骨骼、脏器、纵膈划分为线性四面体实体单元(总数为X,节点数为N),用三角形壳单元(总数为Y,节点数为N)划分皮肤和周围肌肉,各部分单元类型和数目如表1所示。骨架和内脏器官组装的有限元模型如图2所示,完整的人体上躯干有限元模型如图3所示,共695 812个单元,其中壳单元9 612个,实体单元686 200个,人体上躯干内各器官和骨架定义为自动单面接触。

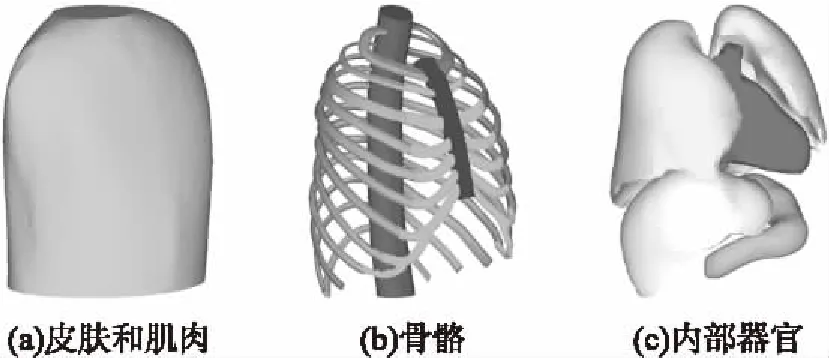
图1 人体上躯干表面模型

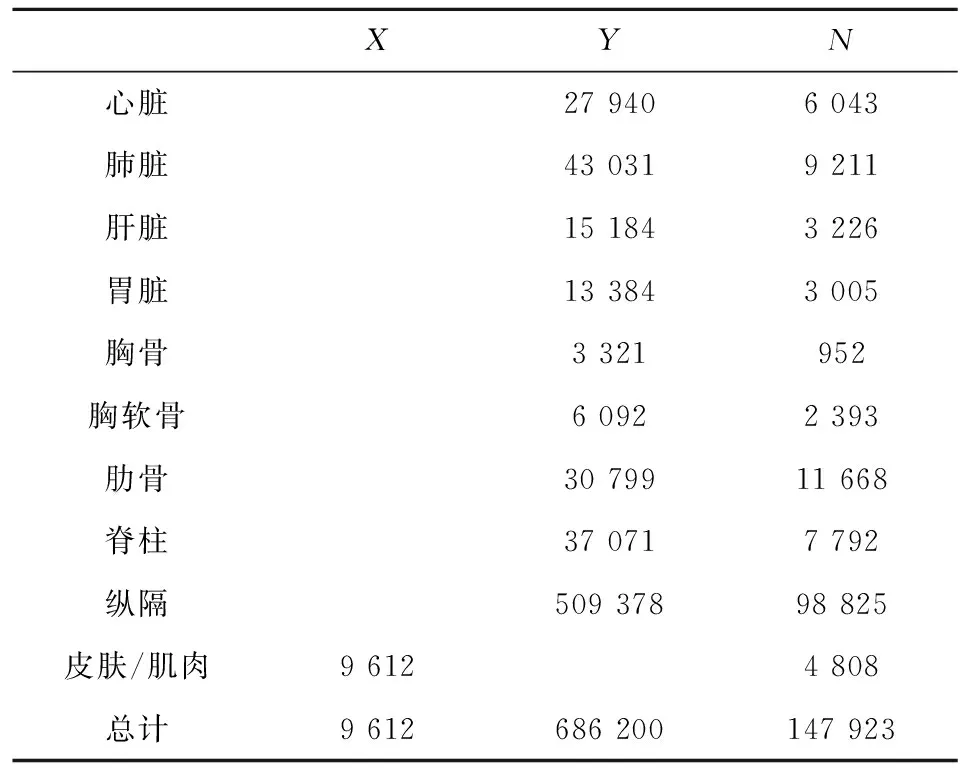
表1 有限元模型各部分的单元数及节点数

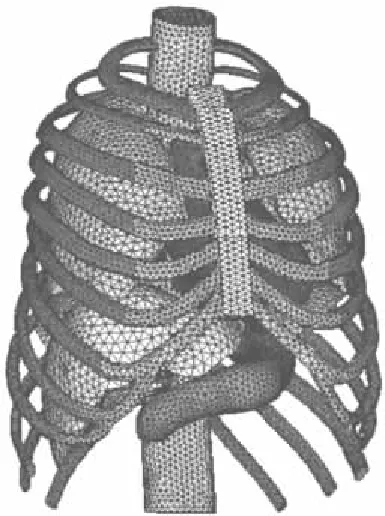
图2 骨架和内脏器官组装的有限元模型

图3 人体上躯干有限元模型

1.2 软硬复合防弹衣和枪弹有限元模型

本文研究的软硬复合防弹衣属于NIJ Ⅳ级防弹衣,它的软内衬材料是超高分子聚乙烯纤维,硬防护面板是硬氧化铝陶瓷,硬防护面板后的背板是高聚乙烯纤维增强树脂基复合材料。

防弹衣计算模型是27 cm×24 cm的弯板,Al2O3陶瓷板厚度为7.6 mm,高聚乙烯复合纤维背板厚度为12 mm,软防护厚度为9 mm,弹丸采用速度为910 m/s的某小口径步枪弹。弹着点取为胸骨正中间位置。软硬复合防弹衣在弹着点5倍弹径范围内采用较密的网格,其余部位的单元沿面内方向按比例逐渐加大。陶瓷板和高聚乙烯背板是硬质固体,被划分为312 000个六面体单元。软防护是由46层的层合材料粘接而成,采用四边形壳单元分层建模,共划分了368 000个单元。步枪弹的被甲、铅套和弹芯的单元类型为六面体网格,共划分单元5 136个,枪弹与软硬复合防弹衣有限元模型如图4所示。

图4 枪弹与软硬防弹衣有限元模型

1.3 材料本构模型

本文采用弹性材料模型描述骨骼材料特性,其中肋骨和胸骨的模型参数采用Caruso[5]等的实验数据,脊柱的模型参数采用Wang[6]和Duck[7]的实验数据。采用粘弹性材料模型描述“肺脏、心脏、肝脏、胃、皮肤以及纵膈”的材料特性,材料模型参数来自Saraf[8]的实验数据。

陶瓷材料采用高速侵彻条件下的断裂损伤模型MA_JOHNSON_HOLMQUIST_ CERAMICS(JH-2)[9]。陶瓷材料参数见表2,表中,ρ为材料密度;G为剪切模量;A,B,C,M,n为材料常数;D1,D2为断裂参数;K1,K2,K3为状态方程参数；T为最大拉伸强度;EH为Hugoniot弹性极限;pH为Hougoniot弹性极限时的压力[9][9]。高聚乙烯复合纤维采用带损伤的复合材料模型MAT_COMPOSITE_ DAMAGE[10]。步枪弹各部分采用Johnson-Cook材料模型,材料参数见文献[10]。

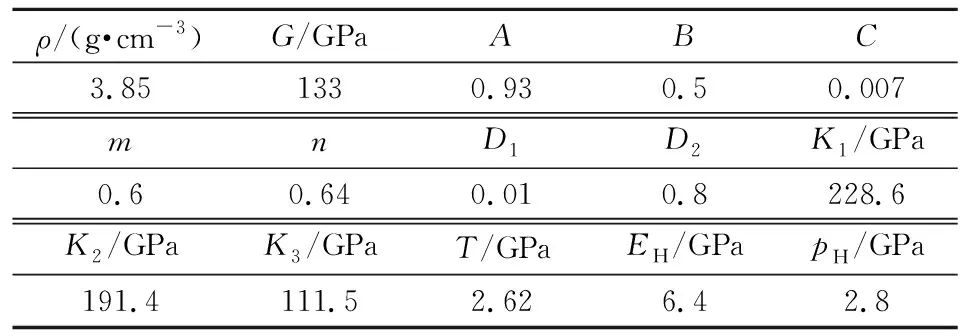
表2 Al2O3陶瓷材料模型参数[9-10]

2 数值计算结果与分析

2.1 模型的实验验证

如图5所示,计算模型由步枪弹、软硬复合防弹衣和人体上躯干靶标3部分定位组装而成,弹着点为胸骨中央前段,撞击速度为910 m/s。实验采用穿有复合防弹衣的假人模拟靶标,假人模拟靶标由仿人胸廓骨骼结构和明胶组成,质量、刚度等物理参数与有限元模型基本相同。某步枪弹以910 m/s高速撞击穿有复合防弹衣的假人模拟靶标,实验弹着点、撞击速度和计算相同,实验结果与有限元模型计算结果比较如表3所示,其中穿透复合防护深度为DC,靶标背板凸起直径为DD,靶标背板凸起高度为DH,胸骨加速度为az,对应的数值模拟与实验结果的相对误差分别为δDC,δDD,δDH,δaz。数值计算结果与实验结果相对误差在16%之内,数值仿真结果和实验结果基本吻合。

图5 穿有软硬复合防弹衣的人体靶标模型

表3 实验数据与数值仿真数据对比

2.2 数值计算结果与分析

2.2.1 侵彻软硬复合防护情况

步枪弹撞击作用下复合防弹衣的破坏与变形过程如图6所示。陶瓷靶板受到弹体的撞击形成陶瓷锥,陶瓷破碎,陶瓷锥不断扩大;弹芯变形墩粗,速度显著下降。陶瓷被破碎侵彻后,弹头继续侵彻背板(高聚乙烯板),冲击波同时向弹道方向和周向传播,使背板和软防护出现鼓包。弹头侵彻导致背板的纤维产生剪切、拉伸断裂等形式破坏,吸收能量,直到弹芯速度为零。因此“陶瓷破碎、背板及软防护层的凸起”是软硬复合防护破坏变形的主要形式。计算发现:在步枪弹侵彻过程中,软硬复合防弹衣最大凸起高度为7.1 mm。在撞击后t=4 μs时刻,防弹衣表面等效应力场呈圆形,直径比枪弹直径略大。随着枪弹逐步侵彻防护层,防弹衣表面等效应力场范围不断扩大,形状为拟圆形,在t=72 μs时,直径是5.6 cm,截面积是24.62 cm2。当t>80 μs时,应力变小,并逐步消失。

图6 复合防弹衣变形过程(v=910 m/s)

2.2.2 人体上躯干靶标皮肤和骨骼的动态响应

图7给出了步枪弹以910 m/s的速度撞击复合靶标后靶标皮肤应力场的演化过程。t=32 μs时刻靶标的皮肤才受到动态应力作用,比复合防弹衣晚了28 μs,表皮应力斑也呈圆形,在弹着点中心应力最大,向四周逐步减少。随后,应力斑面积逐渐增大,应力斑的最大直径出现在t=400 μs时,直径为13.8 cm,面积为149.5 cm2,此时最大应力为0.058 MPa。

图8给出了步枪弹以910 m/s的速度撞击后靶标骨架应力场的情况。在靶标出现应力作用后,骨架出现应力波作用(t>32 μs)。由于骨架的刚度比表皮大,其应力场并不是像表皮那样从冲击点开始以近似圆形向四周变化,而是从撞击点开始沿胸骨往上下两边扩散。在t=100.0 μs时出现最大应力斑,此时最大应力值为14.4 MPa。

图7 上躯干靶标表皮等效应力场变化情况

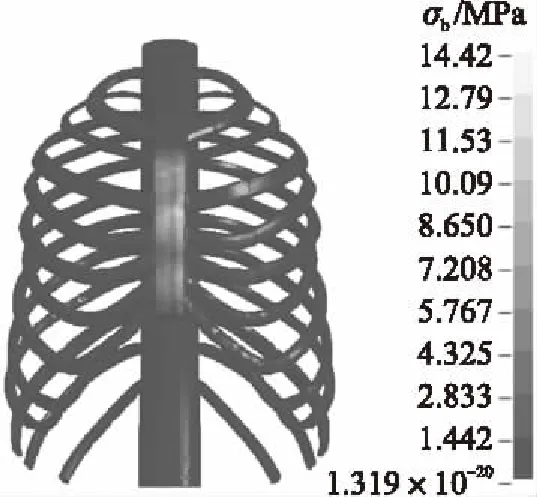
图8 910 m/s撞击后的靶标骨骼应力场情况(t=100 μs)

加速度损伤也是损伤评估的指标之一,弹着点胸骨加速度随时间变化曲线如图9所示,最大加速度峰值为19 649g,脉宽为29 μs,说明人体靶标骨架系统受到强烈的加速度冲击作用。从图9可看出,到达最大加速度后数值就上下波动,做阻尼运动并最终减为0,这是骨架采用粘弹性材料模型的结果。

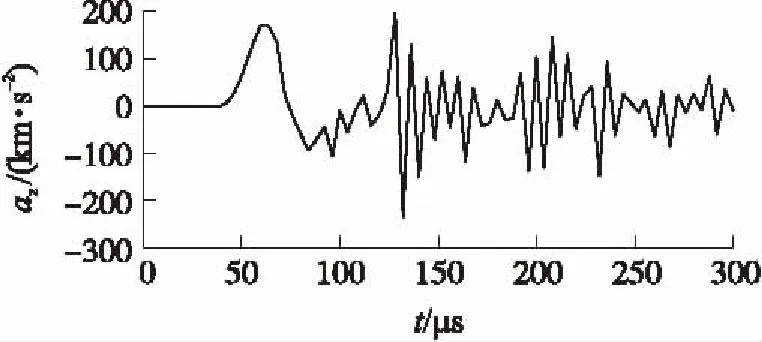
图9 胸骨加速度曲线

2.2.3 主要内脏器官的压力响应情况

由于压力传递和作用与心脏、肺脏、肝脏、胃等器官钝性损伤呈显著的正相关关系,本文在各个脏器选取典型网格单元测量压力值,具体压力测量和取值点见图10。步枪弹高速撞击穿有软硬复合防弹衣的人体上躯干靶标模型,穿透陶瓷面板后仍具有一定动能,继续侵彻背板,直到速度减为0。尽管软硬防弹衣能拦截枪弹,但撞击产生的压力波仍会通过防护材料传递到人体。压力波从弹着点由近及远向四周传递,依次传递到心脏、肺脏、肝脏和胃。图11所示为典型脏器压力云图(t=122 μs)。

图10 弹着点和压力取值位置

图11 t=122 μs时主要器官上的压力场云图

各内脏器官的压力-时间曲线如图12所示,压力波在t=40 μs时传递到心脏。计算发现心脏压力场以撞击点为中心,以近似圆形向四周传播;心脏压力出现时刻比骨架滞后了8 μs。压力波在t=48 μs时传播到肺脏,在t=64 μs时传播到肝脏,在t=68 μs时传播到胃;在t=140 us时,心脏压力斑最大,面积约为38.46 cm2。心脏压力在122 μs出现峰值,为0.95 MPa,压力脉冲宽度为51 μs;肺脏于159 μs出现最大值,为0.22 MPa;肝脏在223 μs出现峰值,为0.18 MPa;胃在246 μs出现峰值,为0.087 MPa,距离弹着点越近的部位压力峰值越大。

图12 器官压力曲线

3 结论

本文建立了步枪弹高速撞击带软硬复合防护的人体上躯干靶标有限元计算模型,给出了人体上躯干的心脏、肺脏、肝脏、胃脏、胸骨、软骨、肋骨、脊柱和表皮等网格划分方法及材料模型;同时还给出了软硬复合防护的氧化铝陶瓷板、高聚乙烯板和软防护的网格划分方法及材料模型。计算结果与实验结果基本吻合,验证了模型的正确性。

对步枪弹高速撞击软硬复合防弹衣的人体上躯干靶标冲击响应进行了数值模拟计算,获得了皮肤、心脏、肺脏、肝脏、胃以及胸骨的动态响应情况,定量揭示了复合防护后人体上躯干靶标动力响应特性和人体上躯干靶内压力的传递机制。弹着点位置为胸骨中间部位的数值计算表明:

①在步枪弹侵彻过程中,对软硬复合防弹衣和皮肤的冲击应力以撞击点为峰值中心,高应力区峰值和面积不断增加;冲击应力沿弹道方向的传递顺序依次为陶瓷面板、高聚乙烯纤维背板、超高分子聚乙烯纤维软质材料内衬、皮肤、骨架和器官。

②软硬复合防护的破坏和变形主要表现为陶瓷破碎、背板及软防护层的凸起。在步枪弹侵彻过程中复合防弹衣最大凸起高度可达7.1 mm。

③人体上躯干靶标表皮上的最大应力斑呈现拟圆形向四周扩散,在t=400 μs时达到最大,直径大约为13.8 cm,面积约为149.5 cm2。

④弹着点胸骨加速度最大达到19 649g,步枪弹通过软硬复合防弹衣对骨架系统产生强烈加速度冲击。

⑤人体上躯干靶标各脏器压力曲线以振荡形式衰减,步枪弹高速撞击软硬复合防弹衣,通过压力波间接损伤人体的内脏器官,其中心脏压力在122 μs时出现峰值,最大可达0.95 MPa。

[1] 王正国,刘宝松,李晓炎.颅脑和胸部撞击伤发生机制研究[J].中国危重病急救医学,2001,13(7):400-403.

WANG Zheng-guo,LIU Bao-song,LI Xiao-yan.Mechanism of craniocerebral and thoracir impact injuries[J].Chinese Critical Care Medicine,2001,13(7):400-403.(in chinese)

[2] BIR C.Development of biomechanical response corridors of the thorax to blunt ballistic impacts [J].Journal of Biomech,2004,37(1):73-79.

[3] ROBERTS J C,MERKLE A C,BIERMANN P J,et al.Computational and experimental models of the human torso for non-penetrating ballistic impact [J].Journal of Biomech,2007,40(1):125-136.

[4] 董萍,张启宽,陈菁.利用有限元研究非贯穿弹道冲击防弹衣后人体躯干的力学响应[J].医用生物力学,2012,27(3):270-275.

DONG Ping,ZHANG Qi-kuan,CHEN Jing.Finite element analysis on mechanical responses of human torso with body armor to non-penetrating ballistic impact[J].Journal of Medical Biomechanics,2012,27(3):270-275.(in Chinese)

[5] CARUSO K S,HIJUELOS J C,BIERMANN P J,et al.Development of synthetic cortical bone for ballistic and blast testing [J].Journal of ADV MATER,2006,38(3):27-36.

[6] WANG H C.Development of a side impact finite element human thoracic model[D].Detroit,MI:Wayne State University,1995.

[7] DUCK F A.Physical properties of tissue[M].London:Academic Press,Harcourt Brace Jovanovich Publishers,1990.

[8] SARAF H,RAMESH K T, LENNON A M, et al.Mechanical properties of soft human tissues under dynamic loading [J].Journal of Biomech,2007,40(9):1 960-1 967.

[9] HOLMQUIST T J,TEMPLETON D W,BOSHNOI R D.Constitutive modeling of aluminum nitride for large strain,high strain-rate,and high-press application[J].International Journal of Impact Engineering,2001,25(3):211-231.

[10] TASDEMICRCI A,HALL I W.Numerical and experimental studies of damage generation in multi-layer composite materials at high strain rates[J].International Journal of Impact Engineering,2007,34(2):189-204.