反向灰色模型的初值优化在道路沉降中应用

吴 彦，张铎强，徐 南

(河海大学 地球科学与工程学院，江苏 南京 210098)

反向灰色模型的初值优化在道路沉降中应用

吴 彦，张铎强，徐 南

(河海大学 地球科学与工程学院，江苏 南京 210098)

针对灰色GM(1,1)模型预测单调递减数据会出现不合理计算误差的问题,建立反向灰色GOM(1,1)模型，利用遗传算法改进x(1)(n)的初始值范围，求出最佳初始值x替换x(0)(1)作为模型初始条件。通过选取高速公路地面沉降数据进行实例计算，证实优化后模型的有效性。

GM(1,1)模型；GOM(1,1)模型；初始条件；遗传算法；道路沉降

灰色预测是灰色系统理论的主要内容之一，GM(1,1)模型是灰色系统理论的基础与核心，被广泛应用于工业、农业、社会经济等领域，成为预报领域的一个重要方法。灰色模型受数据随机性的影响较大，当原始数据呈单调增加时，应用GM(1,1)模型较合理；对于单调递减的数据列，采用反向累加序列的灰色模型，较好地克服这些问题。

本文在灰色预测模型的基础上，研究改进反向灰色模型，应用于道路沉降的监测中。首先利用原始数据建立反向灰色模型GOM，然后利用遗传算法改进x(1)(n)的初始值范围，求出最佳初始值x替换x(0)(1)作为新模型的初始条件，进一步优化反向GOM(1,1)模型，进而求出新的预测值。通过数据比较表明优化后的模型预测精度更高，具有一定的应用价值。

1 原始GM(1,1)模型

1.1 GM(1,1)模型的建立

设非负原始序列X(0)={x(0)(1),x(0)(2),…，x(0)(n)}，X(0)一次累加生成序列X(1)={x(1)(1),x(1)(2),…，x(1)(n)}，其中，

(1)

当X(1)={x(1)(1),x(1)(2),…，x(1)(n)}是时间t的连续可微函数并满足一阶微分方程

(2)

则GM(1,1)模型的响应函数为

(3)

x(0)(k)的预测值为

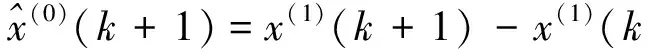
(4)

1.2 GM(1,1)应用前提

对GM(1,1)模型中的参数a，b的求解提出改进方法。事实上，并非所有的非负数据都适合建立GM(1,1)模型。当原始数据具有指数增长趋势时，采用灰色GM(1,1)模型进行分析预测是合理的；当原始数据具有单调递减趋势时，采用反向灰色GOM(1,1)模型进行预测。对于沉降这样一个动态过程或动态系统而言，沉降序列一般开始变化较大，后来变化较小且逐渐趋于稳定，越新的数据更能代表系统当前的状态和未来的发展趋势。采用改进的反向累加生成建立的反向GOM(1,1)模型会更合理，更有利于长期准确预报。

2 初始值的反向优化

2.1 反向累加运算

针对灰色GM(1,1)模型预测单调递减数据会出现不合理计算误差的情况，宋中民等提出反向累积生成灰色GOM(1,1)模型，拓展灰色预测模型的形式，使灰色预测的精度得到提高。

设非负递减原始序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，X(0)的一次反向累加生成序列X(1)={x(1)(1),x(1)(2),…,x(1)(n)}，其中，

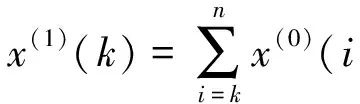
(5)

反向累减式：

x(0)(k)=x(1)(k)-x(1)(k+1).

(6)

若x(1)具有递减趋势，满足微分方程

(7)

称为反向GOM(1，1)模型，a，b通过最小二乘法求得，用GOM(1,1)模型进行拟合、预测。

GOM(1,1)的灰色模型为

(8)

2.2 初始值的优化

灰色模型以x(0)(1)为预测模型的初始值，这些数据比较陈旧。根据新信息对认知的作用大于旧信息的原理，通过遗传算法对以x(1)(n)为初始值范围进行改进，求出最佳初始值x替换x(0)(1)作为模型的初始条件。

遗传算法是一种高效的全局性搜索优化算法，它能在自适应地操作搜索进度的同时自动地寻找并获取搜索空间的相关知识，最终取得最优解。

图1 初始值优化流程

3 实 例

选取某软土路基，路段每100 m设置一个沉降观测断面，每隔半个月观测一次。对其中一个断面的10期变形实测数据，分别采用优化后的GOM(1，1) 模型和反向GOM(1，1)模型利用监测点前7期的数据建模对后3期进行预测，并将预测值与实测数据进行比较，检验模型的预报精度。

图2是变形监测点的10期沉降数据随时间变化的序列图，看出实测数据具有明显的下降趋势。图3是通过遗传算法寻找最优初值的过程。表1为两种预报模型的预测值与实测值的比较，表2给出预报模型的精度分析。

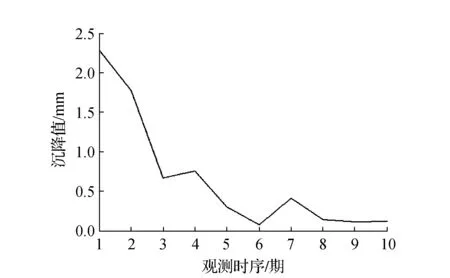
图2 沉降数据分布曲线

图3 寻找初值最优值

表1 优化模型与反向灰色模型计算结果对比

表2 两模型残差值个数统计

从表1、表2分析可以看出，优化后的反向GOM(1,1)模型具有较好的预测效果、较高的预测精度，可以用于沉降监测。

4 结束语

道路沉降的变形因素有多种，若采用不合适的方法建立模型进行预测，不能得到预期的效果。本文在传统灰色模型的基础上，通过优化模型的反向初始值，利用遗传算法改进x(1)(n)的初始值范围，求出最佳初始值x替换x(0)(1)作为模型的初始条件。结合实例计算证实改进后的优化GOM(1,1)灰色模型有效地提高预测精度，具有一定的实用价值。

[1]孟德光，张立山，刘明远．应用灰色模型预测沉降的一种改进方法[J]．南昌工程学院学报，2009(4)：30-33．

[2]党耀国，刘思峰，刘斌．以x(1)(n)为初始条件的GM模型[J]．中国管理科学，2005，13(1)：132-134．

[3]杨晓松，张双成.新陈代谢GM(1,1)模型在建筑物沉降监测中的应用[J].交通科技与经济，2014，16(5)：100-102.

[4]何霞,刘卫锋．两个初值修正灰色GOM(1,1)模型及其等价性研究[J]．杭州师范大学学报：自然科学版,2011,10(3):217-222．

[5]马符讯，徐南，马成.自适应变异粒子群优化灰色模型在变形分析中的应用[J].测绘工程,2014,23(5):55-57．

[6]宋中民,邓聚龙．反向累加生成及灰色GOM(1，1)模型[J]．系统工程，2001，19(1)：66-69．

[7]宋中民，肖新平．反向累加生成及灰色GOM(1，1)模型[J]．武汉理工大学学报：交通科学与工程版，2002，26(4)：531-533．

[8]喜文飞，史正涛.基于卡尔曼滤波的动态灰色理论模型研究[J].测绘工程，2014，23(3)：24-27.

[责任编辑：张德福]

Initial value optimization of opposite grey model and its application to road surface subsidence prediction

WU Yan，ZHANG Duo-qiang，XU Nan

(School of Earth Sciences and Engineering，Hohai University，Nanjing 210098，China)

According to the problem that the grey GM(1,1) model may has unreasonable calculation errors during predicting monotone decreasing dates，an opposite grey GOM(1,1) model is made by using the genetic algorithms to improve the range of initial value based onx(1)(n) and seek a best one as the initial condition of the model. An example of highway subsidence is selected to be tested in order to confirm that the improved model is effective.

GM(1,1) model;GOM(1,1) model;initial condition;genetic algorithm;road subsidence

2013-09-27;补充更新日期：2014-10-31

河海大学大学生创新训练计划(201205xcx175)

吴 彦(1991-)，男，本科.

TU196

：A

：1006-7949(2014)12-0060-03