基于选权迭代法的抗差整体最小二乘及其应用

杨勇喜,贾东振,何秀凤

(河海大学 卫星及空间信息应用研究所，江苏 南京 210098)

基于选权迭代法的抗差整体最小二乘及其应用

杨勇喜,贾东振,何秀凤

(河海大学 卫星及空间信息应用研究所，江苏 南京 210098)

在测量数据处理中，观测向量与系数矩阵同时存在偶然误差时，整体最小二乘法能够得到更高精度的参数解,但整体最小二乘法无抗差能力，观测向量中的粗差将对参数求解产生较大影响。为解决上述问题，采用拉格朗日极值法推导了基于选权迭代法的抗差整体最小二乘计算公式,通过三维坐标转换参数求解实例对3种选权迭代法进行分析。结果表明,IGG法在抗差整体最小二乘解法中抗差效果最好。

粗差；抗差整体最小二乘；选权迭代；三维坐标转换；IGG法

测量平差参数求解中，观测向量仅存在偶然误差时，可采用最小二乘法(LS)求得参数的最优解。若观测向量存在粗差，则采用抗差最小二乘法(抗差LS)剔除或减弱粗差的影响[1]。对于系数矩阵和观测向量同时存在偶然误差的情况，需要采用整体最小二乘方法。整体最小二乘问题首先由Golub和Van Loan[2]提出，并给出了奇异值分解的解法。后来Schaffrin提出了基于拉格朗日求极值的迭代法[3]。魏木生[4]、俞锦成[5]等对整体最小二乘理论进行了深入细致的研究。实际应用领域，如线性回归[6]、空间后方交会[7]、建筑物沉降预测[8]等，整体最小二乘法均能够得到更合理、更高精度的解。但是整体最小二乘方法没有抗差能力，如果观测向量存在粗差，参数估计将会偏离实际[9-10]。将选权迭代法应用于整体最小二乘法的抗差估计，可以有效地抵御粗差对参数估计的影响。陈玮娴[11]、陈义[12]等都曾将选权迭代法应用于三维坐标转换的整体最小二乘估计，但是选权迭代法有多种形式，哪种形式最有效，现有文献鲜有提及。本文推导了基于选权迭代法的抗差整体最小二乘计算公式，并通过三维坐标转换对不同的选权迭代法进行了对比和分析。结果表明，IGG法抗差效果最好。

1 数学模型

1.1 抗差整体最小二乘法

对于观测方程L=AX，当观测向量L与系数矩阵A独立时，EIV(Errors-In-Variables)模型[13]为

L-eL=(A-EA)X.

(1)

式中：L∈Rm×1为观测向量，eL∈Rm×1为观测向量的偶然误差，A∈Rm×n为系数矩阵(列满秩)，EA∈Rm×n为系数矩阵的偶然误差，X∈Rn×1为待求参数。对应的随机模型

(2)

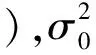
L-AX0-Aδx-eL+BeA=0.

(3)

式中B=(X0)T⊗Im，Im∈Rm×m。

整体最小二乘的目标函数为

(4)

(5)

式中，ρ(eL(i))为M估计中选取的函数。利用拉格朗日求极值的方法，建立拉格朗日函数[11]

2λT(L-AX0-Aδx-eL+((X0)T⊗Im)eA).

(6)

对上式求eL偏导数，并令其为0。

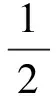
(7)

(8)

类似地，式(6)分别对eA,λ,δx求偏导数，令其为0，并求出极值点

(9)

L-AX0-Aδx-eL+BeA=0,

(10)

(11)

(12)

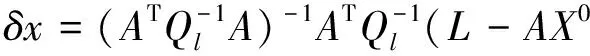
(13)

由以上推导，结合文献[11]，得到如下的计算步骤(上标i为第i步迭代)：

1)设置初值

2)从i=0开始，依次计算

⊗Im,

(14)

根据式(13)得

(15)

并计算

X(i+1)=X(i)+δx(i+1),

(16)

(17)

(18)

1.2 常用选权迭代法

选权迭代法在抗差估计中应用广泛，常用的有以下3种形式。

1.2.1 胡贝尔法(Huber)

胡贝尔法确定的权因子为

(19)

当所有改正数均在-c和c之间时，胡贝尔估计就是经典的最小二乘估计。而当改正数大于c时，其w(v)与改正数成反比，v越大，对应的w(v)越小，权也越小，与此相应该观测值对参数估计的影响也越小。

1.2.2 汉佩尔法(Hampel)

汉佩尔法确定的权因子为

(20)

1.2.3 IGG法

IGG法是周江文在1989年提出的一种抗差权函数构造方法[14]，对应的权因子为

(21)

2 算例及分析

采用文献[15]中的七参数坐标转换模型，求解WGS-84坐标系和北京54坐标系下三维坐标的转换参数。根据前面的求解步骤，计算分析不同选权迭代形式的抗差整体最小二乘法的结果。

表1给出了5个已知点在WGS-84和北京54坐标系下的坐标值，根据布尔莎模型求解WGS-84和北京54坐标系之间的转换参数。

首先采用最小二乘方法和整体最小二乘方法对七参数求解，然后在#1点的X坐标加入3 m的粗差，再采用两种方法求解，结果见表2。

表1 已知点在WGS-84坐标系和北京54坐标系下的坐标值 m

表2 LS和TLS参数计算结果

由表2可知，未加入粗差时整体最小二乘方法的估计结果比最小二乘方法的精度高。加入粗差后，最小二乘方法和整体最小二乘方法均严重偏离了结果。

采用抗差整体最小二乘方法对加入粗差后的坐标进行参数估计。抗差估计中的选权迭代方法依次采用胡贝尔法、汉佩尔法和IGG法。对于胡贝尔法设计4个方案。方案1：c=σ；方案2：c=1.5σ；方案3：c=2σ；方案4：c=2.5σ。参数计算结果如表3所示。

表3 胡贝尔法各方案比较

由表3可以看出，方案3即c=2σ时抗差估计效果最佳，当c=2.5σ时与含粗差的整体最小二乘方法计算结果一致。

对于汉佩尔方法也设计4个方案。方案1：a=σ,b=1.5σ,c=3σ；方案2：a=1.5σ,b=2σ,c=4σ；方案3：a=2σ,b=2.5σ,c=5σ；方案4：a=2.5σ,b=3σ,c=6σ。参数计算结果如表4所示，方案1的抗差估计效果最佳。对于IGG法，k依次取1,10-1,10-2,10-4。参数估计结果如表5所示。

表4 汉佩尔法各方案比较

表5 IGG法各方案比较

由表5中数据可知，k的取值对结果影响很小，这与文献[1]中的论述是一致的。

由上面的计算可知，3种选权迭代方法都有抵御粗差的能力，胡贝尔法方案3与汉佩尔法方案1的结果接近，但精度稍差；IGG法精度最高。IGG法从测量误差理论来看，如果数据中只含有偶然误差，界限mσ中m取1.5(在±1.5σ之外的概率仅为0.13)，这个区间以外的观测值既不能完全排除又要限制其有害的影响。当超过2.5σ(概率为0.01)，认为是粗差，给予淘汰。IGG方案充分考虑了测量数据的实际情况，是一种十分有效的抗差方案。

3 结 论

为解决观测向量中粗差对整体最小二乘结果产生显著影响的问题，本文首先采用拉格朗日极值法推导了基于选权迭代法的抗差整体最小二乘计算公式，然后通过三维坐标转换参数求解实例对3种选权迭代法进行了分析，得出以下结论：

1)在不含粗差情况下，整体最小二乘法比最小二乘法有更高精度的参数解，但是整体最小二乘法没有抵御粗差的能力，需要加入抗差算法。

2)选权迭代法应用于整体最小二乘法，可以较好地抵御粗差的影响，但是抗差能力有差异。计算结果表明，胡贝尔法与汉佩尔法抗差能力相当，IGG法抗差能力最好。

[1]周江文,黄幼才,杨元喜. 抗差最小二乘法[M]. 武汉：华中理工大学出版社,1997.

[2]GOLUB G H,VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis.1980,17(6):883-893.

[3]SCHAFFRIM B. A note on Constrained Total Least-Squares Estimation[J]. Linear Algebra and Its Applications,2006,417:245-258.

[4]魏木生. 广义最小二乘问题的理论和计算[M]. 北京:科学出版社,2006.

[5]俞锦成. 关于整体最小二乘问题的可解性[J]. 南京师范大学学报:自然科学版,1996(1):12-16 .

[6]鲁铁定,陶本藻,周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报:信息科学版, 2008,33(5):504-507.

[7]陈义,陆珏,郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报:信息科学版,2008,33(12):1271-1274.

[8]袁豹,岳东杰, 李成仁. 基于总体最小二乘的改进 GM (1, 1) 模型及其在建筑物沉降预测中的应用[J]. 测绘工程, 2013, 22(3): 52-55.

[9]龚循强，刘国祥，李志林，等.总体最小二乘拟合问题求解方法的比较研究[J].测绘科学，2014，39(9)：29-33.

[10]邓兴升，孙虹虹，汤仲安.高斯牛顿迭代法解算非线性Bursa-Wolf模型的精度分析[J].测绘科学，2014，39(5)：93-95.

[11]陈玮娴,袁庆. 抗差总体最小二乘方法[J]. 大地测量与地球动力学,2012,32(6):111-114.

[12]陈义,陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报,2012,41(5):715-722.

[13]YUNZHONG SHEN, BOFENG LI, YI CHEN. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy. 2011,85(4): 229-238.

[14]张勤,张菊清,岳东杰. 近代测量数据处理与应用[M] 北京:测绘出版社,2011.

[15]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉:武汉大学出版社,2003.

[责任编辑：刘文霞]

Robust total least-squares based on selecting weight iteration method and its application

YANG Yong-xi，JIA Dong-zhen，HE Xiu-feng

(Institute of Satellite Navigation and Spatial Information System, Hohai University,Nanjing 210098,China)

In the measurement data processing,total least squares method can get more accurate parameter solution when observation vector and the coefficient matrix all exist random errors. But total least squares method doesn’t have the ability to resist the gross errors,which will have great impact on parameters. To solve the above problem,it minimizs the target function of classical Lagrange approach and deduces the robust total least-squares estimation calculation formula based on selecting weight iteration.Then the three selecting weight iteration methods are applied to three-dimensional coordinate transformation. The results show that IGG method works best in the robust total least-squares method.

gross errors; robust total least-squares method; selecting weight iteration; 3D coordinate transformation; IGG method

2013-11-27;补充更新日期：2014-10-15

国家自然科学基金资助项目(41274017)；江苏省科技支撑计划资助项目(BE2010316)

杨勇喜(1989-)，男，硕士研究生.

P207

：A

：1006-7949(2014)12-0056-04