利用Bayes判别分析进行矢量地图修改检测
郭建忠,谢明霞,2,陈 科
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.75719部队,湖北 武汉 430074)
利用Bayes判别分析进行矢量地图修改检测
郭建忠1,谢明霞1,2,陈 科1
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.75719部队,湖北 武汉 430074)
针对现有的矢量地图修改检测方法计算速度慢、效率低等问题,设计利用Bayes判别分析进行地图修改检测的方法。首先对同一幅修改前后的矢量地图分别进行栅格化,并进行配准;然后利用Bayes判别分析方法对配准后的栅格图像进行变化检测,获得矢量地图的修改区域;最后将修改区域与审校结果进行对比,发现错修改和漏修改问题。实际矢量地图数据的修改检测实验结果验证了利用Bayes判别分析方法实现地图修改检测的有效性和可行性。
矢量地图;Bayes判别分析;变化检测
在矢量地图生产中,经常会遇到地图在审校修改过程中,由于制图人员的疏忽和误操作将原地图数据中正确地方进行了改动(误删或者误移)等问题,严重影响了矢量地图生产成果的质量。矢量地图的整个生产过程无论过去、现在以至不久的将来都将无法也不可能摆脱人的主观因素的影响,错误的发生是不随人的主观意志而转移的,制图生产单位只能采取有效的层层把关措施严格限制这种错误,但无法完全、彻底地排除错误的发生。因此,如何利用现有的技术提供或编制对矢量地图修改前后进行对比分析的工具,从而辅助制图人员在地图修改过程中及时、有效地发现错修改或漏修改地方显得尤为重要。
在检测矢量地图修改情况时,通常采用要素遍历、坐标比较等方法,这类针对矢量地图要素及其坐标的方法,当地图要素较多时,其计算速度慢,且效率较低[1]。针对这一不足,本文首先对基于最大后验概率准则的Bayes判别分析进行了介绍,然后设计利用Bayes判别分析进行矢量地图修改检测的方法流程,最后将此方法应用于实际生产过程中的矢量地图修改的前后对比。实际矢量地图数据的修改检测实验结果验证了本文利用Bayes判别分析方法实现地图修改检测的有效性和可行性。
1 基于最大后验概率准则的Bayes判别分析
1.1 最大后验概率准则
设有k个类π1,π2,…,πk,且类πi的概率密度函数为P(x|πi),样品x来自类πi的先验概率为pi,i=1,2,…,k,满足p1+p2+…+pk=1。利用Bayes理论,则可认为变量x服从一个包含各类密度成份的混合密度分布,其概率密度函数为
).
(1)
x属于πi的后验概率(即当样品x已知时,它属于πi的概率)为

(2)
最大后验概率准则采用如下的判别规则[2]:

(3)
1.2 先验概率与概率密度函数的求解
先验概率可以根据类的大小、历史资料及经验等加以确定,常常带有一定的主观性。利用先验信息来进行判别是Bayes判别的一大特点。
对于概率密度函数的求解,一般通过对其样本直方图进行拟合获得其大致分布类型,在假设样本分布符合该分布类型的前提下,根据样本值对分布函数中各未知参数进行参数估计(如EM算法、Bayes点估计法、区间估计等),对获取的参数估计值进行参数分析(该过程可以通过SPSS软件完成),所得的分析结果若满足一定的值域内,则假设成立,根据参数估计值获得样本的概率密度函数[3-4]。
2 利用Bayes判别分析进行矢量地图修改检测
矢量地图是一个综合的要素集,包括地物的几何(形状)数据、属性数据和拓扑数据[1]。由于地图直观显示的是地物的几何特征,因此,本文的研究仅针对矢量地图几何数据的修改检测。
传统的采用逐要素遍历的方法对矢量地图进行修改检测时,首先要将修改前后的各要素进行对应,无法对应的要素即为新增或删除的要素;要素对应后,对成对要素中的坐标进行判断,若坐标不同,即为发生位移的要素。在此过程中,要素的对应和坐标的判断都不易实现,且当要素数量较多时,采用要素遍历方法对矢量地图进行修改检测需
要花费较长的时间,其检测精度和速度都无法满足实际应用的需要[5-7]。本文将矢量地图修改检测问题转化为图像的变化检测问题,抛开了矢量地图中的要素概念,将要素问题转化为像素问题,其实质就是要将同一幅地图数据修改前后的差异图像中的像元分为两类——变化像元类πc和未变化像元类πn,判断每个像元属于哪一类并标上相应的类别标记,从而生成一幅将变化区域与未变化区域区分开来的地图修改检测结果图。因此,修改区域提取实际上可以理解为典型的两类判别分析问题。在实际的地图生产过程中,利用Bayes判别分析进行矢量地图修改检测方法的具体流程如下(相应流程如图1所示):
Step 1:对同一幅修改前后的矢量地图数据分别进行出版处理,得到相应的栅格图像;
Step 2:对两幅栅格图像进行配准;
Step 3:根据先验信息获取地图修改前后变化类πc和未变化类πn的先验概率pc和pn;
Step 4:根据各类的样本直方图获得大致的总体分布,根据1.1节中所介绍的概率密度函数的求解方法获得各类的参数估计值及概率密度函数P(x|πc)和P(x|πn);
Step 5:利用获得的先验概率和概率密度函数根据式(2)计算相应的类的后验概率函数P(πc|x)和P(πn|x);
Step 6:对未标识样本集中的各样本进行判别,
Forx(x∈未判别样本集) 分别计算P(πc|x)和P(πn|x); If(P(πc|x)>P(πn|x)) Thenx∈πc; Elsex∈πn至下一个未标识样本;
End For
即计算各样本属于各类的后验概率值,样本属于所计算的各类后验概率最大的一类;
Step 7:根据变化检测结果获得矢量地图修改区域,将其与审校结果进行对比分析,发现矢量地图错修改和漏修改问题。
3 实验分析
3.1 矢量地图修改检测
选取某地区的地图数据,将修改前后的数据分别生成eps或其它数据格式的图像(如jpg、bmp等),如图2所示。

图1 利用改进Bayes判别分析进行地图修改检测流程
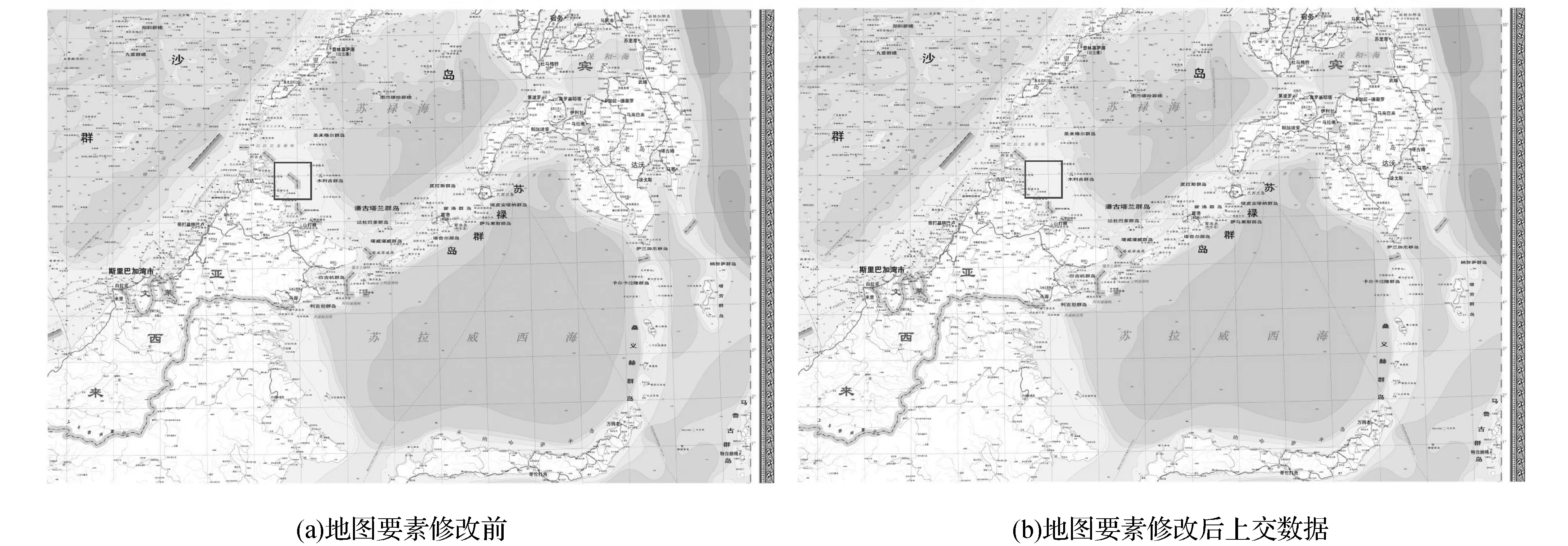
图2 实验数据(方框标识的为误修改部分)
由于地图修改前后的eps图像的差异图像主要分为变化和未变化两部分,因此,差异图像的直方图中将存在两个波峰,由于变化部分相对于未变化部分要少得多,故一个波峰明显,另一个波峰则相对很隐蔽。由于未变化类别的像元值较小,将主要集中在直方图的左边界附近,而变化类别的像元值较大,分布在靠近直方图右边界的范围上[8]。基于这一特点,可以选取两个阈值Tn和Tc,选取方法如下:
Tn=MD(1-α),Tc=MD(1+α).
(4)
式中:MD为地图修改前后差异图像中像元的中值,(MD=(max{XD}-min{XD})/2),α∈(0,1)为权重调节因子,分别以两个像元子集
πn={X(i,j)|X(i,j) πc={X(i,j)|X(i,j)>Tc} (5) 作为未变化类和变化类两类像元的初始样本集,而没有被这两个子集所包含的像元则被标记为无标识样本,即Tmin=Tn,Tmax=Tc,如图3所示,其中,X(i,j)表示差异影像上第i行第j列的像元值。对于地图修改前后变化类和未变化类的先验概率,可通过差异图像中像元的中值获取,即分别计算差异影像中大于等于或者小于MD的像元的个数为Nc和Nn,则 (6) 其中,N为差异影像中像元的总个数。 图3 两类像元初始子集的确定 根据变化和未变化像元类的正态分布特性估计其参数值,从而获得两类的后验概率密度函数,对未标识像元值进行判别、循环、更新、再判别,直至所有未标识像元值判别完毕。利用Bayes判别分析进行地图修改检测的结果如图4所示。将变化检测结果与审校结果进行对比,可以发现此处修改为作图人员的误删除,通过对矢量地图的快速修改检测,可以对地图修改过程中存在的问题进行及时发现,从而较大程度避免了地图错漏修改问题的存在,有效提高了地图成图质量。利用本文提出的改进Bayes判别分析方法能够有效地进行地图修改检测。 图4 利用改进Bayes判别分析进行地图修改检测结果(方框中标识的为检测到的地图修改部分) 3.2 效率分析 以上实验所选取的矢量地图数据包含1万多要素(点、线、面要素),采用传统的逐要素遍历的方法对矢量地图进行修改检测时,需要对修改后的各点、线、面要素与修改前的各点、线、面要素进行一一对比检查,若找到与其相对应的要素,则需再进行坐标检查,判断该要素是否发生位移变化;若未找到对应要素,则判断该要素为新增要素。修改前后各要素一一对比检查完后,修改前矢量地图数据中未对应要素即为被删除要素。假设某幅矢量地图数据包含N个要素,从以上过程中可以看出,采用逐要素遍历的方法至少需要遍历N次(即每个要素检查一次找到对应要素),若每检查一个要素需要1 s,则检测一幅矢量地图需要花费的时间至少在小时级,且当属性数据相同,几何数据接近的两要素发生位移时,采用逐要素遍历的方法无法对修改前后的要素进行对应。同等情况下,对1 000×1 000像素的图像进行变化检测的时间大约需要十几秒,当图像较大时,可以对其进行分割,逐块并行检测,然后对检测结果进行拼接。采用传统的逐要素遍历的方法,很难实现根据要素对矢量地图进行分割,一方面由于对修改前后矢量地图中各要素进行对应较困难,即分割点不容易获取;另一方面,对于新增和删除的要素,在分割结点前后容易出现误判断的情况。 本文将地图制图过程中对要素进行修改时是否存在要素的误移、误删、误增等问题转化为对修改前后地图数据生成的eps或其它数据格式的图像的变化检测问题,通过对实际地图数据的修改检测实验验证了本文提出的利用Bayes判别分析进行矢量地图修改检测方法的有效性和在地图制图过程中使用的可行性。 [1]李宇光,李连营,李清泉,等.基于栅格化思想的矢量电子地图几何变化检测[J].地理空间信息,2010,8(1):142-146. [2]王学民.应用多元分析[M].上海:上海财经大学出版社,2004:138-155. [3]卢纹岱.SPSS for Windows 统计分析[M].北京:电子工业出版社,2007:647-651. [4]李亚平,杨华,陈霞.基于EM和BIC的直方图拟合方法应用于遥感变化检测阈值确定[J].遥感学报,2008(1):85-91. [5]李连营,李清泉,赵卫锋,等.导航电子地图增量更新方法研究[J].中国图象图形学报,2009,14(7):1238-1244. [6]徐敬海,李清泉.基于时态GIS的导航电子地图增量更新研究[J].武汉大学学报:信息科学版,2008,33(11):1182-1185. [7]吴中恒.导航电子地图数据变化自动检测模型与方法[D].武汉:武汉大学,2006. [8]陈科,张保明,谢明霞.模糊Bayes理论在遥感影像变化检测中的应用[J].计算机工程与应用,2010,46(19):185-188. [责任编辑:刘文霞] ModificationdetectionforvectormapbasedonBayesdiscriminantanalysis GUO Jian-zhong1,XIE Ming-xia1,2,CHEN Ke1 (1.School of Geospatial Information Engineering,Information Engineering University,Zhengzhou 450052,China;2.Troups 75719,Wuhan 430074,China) Aiming to the problem of heavy running time performance in the common used method for modification detection between vector maps,a method based on Bayes is proposed.First,the unmodified and modified vector maps are put into the grid images and the registration.Then the change detection for grid images is done in order to achieve the modified region.Finally,the problems of inaccurate modification and missed modification are pointed according to the comparison between the modified region and examing results.The experimental result of modification detection for real vector map proves the validity and practicability of the proposed method. vector map;Bayes discriminant analysis;change detection 2012-10-30 国家自然科学基金资助项目(41271392) 郭建忠(1968-),男,教授,博士. P28 :A :1006-7949(2014)01-0001-04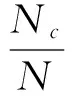


4 结束语

