带有Banach代数的锥度量空间中的一类公共不动点定理
黄华平,胡松林,明 巍, 周 惠
(1.湖北师范学院 数学与统计学院, 湖北 黄石 435002;2.黄石二中 数学组,湖北 黄石 435003)
带有Banach代数的锥度量空间中的一类公共不动点定理
黄华平1,胡松林1,明 巍1, 周 惠2
(1.湖北师范学院 数学与统计学院, 湖北 黄石 435002;2.黄石二中 数学组,湖北 黄石 435003)
首先介绍了带有Banach代数的锥度量空间的相关概念,然后给出此空间中的一类公共不动点定理,并且举例说明其应用.
锥度量空间;广义Lipschitz常数;弱相容的
自从2007年黄龙光[1]等人引入了锥度量空间的概念,延拓了普通的度量空间,并且在此基础上推广了著名的Banach压缩映像原理以来,许多学者致力于此空间中不动点及公共不动点定理的研究工作. 在此基础上,如雨后春笋,近几年已经涌现出了大量的杰出的工作(见文献[2~7]). 然而,从2012年开始,关于锥度量空间上的不动点定理的研究已不再成为热门课题. 究其原由,是因为最近已有学者[8~9]通过作出一个从锥度量空间到度量空间的映射,证明了锥度量空间中有很多不动点结果可以原封不动地直接由度量空间中的相应结果平移过来,也就是说,锥度量空间中的很多结果实质上是和度量空间中的相关结果是等价的. 这一发现使得锥度量空间中的不动点的研究继续进行下去步履维艰.
2013年11月,刘浩[10~11]等人首次引入了带有Banach代数的锥度量空间,证明了在此空间上的不动点结果和度量空间中相应结果并不是等价的,而且很有理论意义和现实意义,这使得学者们把目光投向于此空间上的不动点结果的研究. 基如此,本文得到了带有Banach代数的锥度量空间中的一类公共不动点定理,并且给出例子验证了我们的结论是很有意义的.
定义1 设A为Banach代数,θ和e分别为A的零元和单位元,P为A的一个非空闭子集,+为非负实数集. 若满足
1){θ,e}⊂P;
2)∀α,β∈+⟹αP+βP⊂P;
3)P2=PP⊂P;
4)P∩(-P)={θ}
则称P为A中的一个锥. 设x,y∈A, 若x≤y⟺y-x∈P和x≪y⟺y-x∈intP, 则称“≤ ”和“≪ ”都为A中的偏序. 如果∀x,y∈A都存在常数M>0,使得
θ≤x≤y⟹‖x‖≤M‖y‖
则称P为A中的正规锥. 而满足上式最小的M称为P的正规常数.
定义2 设X为非空集,A为Banach代数. 假定映射d:X×X→A满足:
i)θ≤d(x,y)(∀x,y∈X),d(x,y)=θ⟺x=y
ii)d(x,y)=d(y,x)(∀x,y∈X)
iii)d(x,y)≤d(x,z)+d(z,x)(∀x,y,z∈X)
则称d为X上的锥度量,而称(X,d) 为带有Banach代数的锥度量空间.
定义3 设 (X,d)为带有Banach代数A的锥度量空间, {xn}⊂X,x∈X, 则

2)若∀θ≪c,总存在自然数N,当n>N时,都有d(xn,xm) ≪c,则称 {xn}为X中的Cauchy列.
3)若X中的每个Cauchy列都在X中是收敛的,则称(X,d) 是完备的.
定义4 设X为非空集,f,g:X→X为两个映射,则
1)若∃x∈X,使得y=fx=gx,则称x为f和g的重合点,而称y为f和g的耦合点.
2)若f和g在它们的任一重合点x∈X处都可交换,即fgx=gfx,则称(f,g) 是弱相容的.

引理2[5]设X为非空集,f,g:X→X为两个映射, (f,g)是弱相容的. 若f和g在X中有唯一的耦合点,则y也是f和g在X中唯一的公共不动点.
定理1 设 (X,d)为带有Banach代数A的锥度量空间,且A有单位元e,P为带有正规常数M的正规锥. 假定映射f,g:X→X满足
d(fx,fy)≤kd(gx,gy),∀x,y∈X
其中k∈P为广义Lipschitz常数,满足ρ(k)<1. 如果f(X) ⊂g(X),g(X) 是X的完备子空间,那么f和g在X中有唯一的耦合点. 并且当(f,g) 是弱相容的,则f和g在X中有唯一的公共不动点.
证明 ∀x0∈X,由条件可作点列{xn}⊂X满足fxn=gxn+1. 由于
d(gxn+1,gxn)=d(fxn,fxn-1)≤kd(gxn,gxn-1)≤k2d(gxn-1,gxn-2)≤…≤knd(gx1,gx0)
于是对∀n>m,由引理1,有
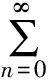
再由P的正规性,有
‖d(gxn,gxm)‖≤M‖(e-k)-1‖·‖km‖·‖d(gx1,gx0)‖
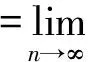
d(gxn,fp)=d(fxn-1,fp)≤kd(gxn-1,gp)
结合P的正规性,有
‖d(gxn,fp)‖≤M‖k‖·‖d(gxn-1,gp)‖→0(n→∞)
从而d(gxn,fp)→θ(n→∞) . 又显然d(gxn,gp)→θ(n→∞) 因此由极限的唯一性有fp=gp. 下证f和g有唯一的耦合点.
用反证法. 假设∃p′≠p,使得fp′=gp′ . 遂有
d(gp′,gp)=d(fp′,fp)≤kd(gp′,gp)≤…≤knd(gp′,gp)
再次运用P的正规性,有
‖d(gp′,gp)‖≤M‖kn‖·‖d(gp′,gp)‖→0 (n→∞)
故d(gp′,gp)=θ, 即gp′=gp.最后由引理2即得f和g有唯一的公共不动点.
定理2 设(X,d) 为带有Banach代数A的锥度量空间,且A有单位元e,P为带有正规常数M的正规锥. 假定映射f,g:X→X满足
d(fx,fy)≤k[d(fx,gx)+d(fy,gy)],∀x,y∈X
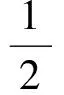
证明 ∀x0∈X,由条件可作点列{xn} ⊂X满足fxn=gxn+1.由于
d(gxn+1,gxn)=d(fxn,fxn-1)≤k[d(fxn,gxn)+d(fxn-1,gxn-1)]=k[d(gxn+1,gxn)+d(gxn,gxn-1)]
故d(gxn+1,gxn)≤hd(gxn,gxn-1)≤…≤hnd(gx1,gx0)
此处h=(e-k)-1k. 由引理1及谱半径的连续性有
遂 ‖hn‖→0(n→∞). 然后类似定理1的证明得到∃q∈g(X),使得gxn→q(n→∞) .由此,∃p∈X,适合gp=q.因为
d(gxn,fp)=d(fxn-1,fp)≤k[d(fxn-1,gxn-1)+d(fp,gp)]
结合锥度量的连续性,上式两端取极限可得d(gp,fp)≤kd(fp,gp),所以
d(fp,gp)≤kd(fp,gp)≤…≤knd(fp,gp)
再由P的正规性,有
‖d(fp,gp)‖≤M‖kn‖·‖d(fp,gp)‖→0 (n→∞)
于是fp=gp.下证f和g有唯一的耦合点.
用反证法. 假设∃p′≠p,使得fp′=gp′ . 遂有
d(gp′,gp)=d(fp′,fp)≤k[d(fp′,gp′)+d(fp,gp)]=θ
导出gp′=gp.最后由引理2即得f和g有唯一的公共不动点.
定理3 设(X,d) 为带有Banach代数A的锥度量空间,且A有单位元e,P为带有正规常数M的正规锥. 假定映射f,g:X→X满足
d(fx,fy)≤k[d(fx,gy)+d(fy,gx)],∀x,y∈X
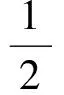
证明 ∀x0∈X,由条件可作点列{xn}⊂X满足fxn=gxn+1. 由于
d(gxn+1,gxn)=d(fxn,fxn-1)≤k[d(fxn,gxn-1)+d(fxn-1,gxn)]≤k[d(gxn+1,gxn)+d(gxn,gxn-1)]
故由定理2类似的方法有∃q∈g(X), 使得gxn→q(n→∞) .由此,∃p∈X, 适合gp=q.因为
d(gxn,fp)=d(fxn-1,fp)≤k[d(fxn-1,gp)+d(fp,gxn-1)]
结合锥度量的连续性,上式两端取极限,所以d(gp,fp)≤kd(fp,gp). 再次由定理2类似的方法有fp=gp. 下证f和g有唯一的耦合点.
用反证法. 假设∃p′≠p, 使得fp′=gp′ .于是
d(gp′,gp)=d(fp′,fp)≤k[d(fp′,gp)+d(fp,gp′)]=2kd(gp′,gp)
因为ρ(2k)=2ρ(k)<1, 所以应用定理1类似的方法得到gp′=gp. 最后由引理2即得f和g有唯一的公共不动点.
例1 设

规定乘积是通常的矩阵乘法,则A为带有单位元e(单位矩阵)的Banach代数. 设X=,定义
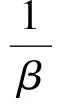
[1]Huang L G,Zhang X.Cone metric spaces and fixed point theorems of contractive mappings[J]. Journal of Mathematical Analysis and Applications,2007,332(2): 1468~1476.
[2]Huang Huaping. Conditions of non-normality in cone metric spaces[J], Mathematica Applicata, 2012, 25(4): 894~898.
[3]韩 艳,黄国华.锥度量空间中非连续扩张映射的公共不动点定理[J]. 湖北师范学院学报(自然科学版),2012,32(1):41~44.
[4]黄国华,石 露. 锥度量空间中扩张映射的公共不动点定理[J]. 湖北师范学院学报(自然科学版),2012,32(3):58~62.
[5]Abbas M, Jungck M. Common fixed point results for noncommuting mappings without continuity in cone metric spaces[J]. Journal of Mathematical Analysis and Applications,2008, 341: 416~420.
[6]Farajzadeh A P.Fixed point theory for generalized contractions in cone metric spaces[J].Commun Nonlinear Sci Numer Simulat,2012,17:708~712.
[7]Hussain N.Common fixed point theorems for generalized contractive mappings with applications[J]. Fixed Point Theory and Applications, 2013,169:1~17.
[8]Kadelburg Z.A note on the equivalence of some metric and cone metric fixed point results[J].Applied Mathematics Letters, 2011,24:370~374.
[9]Asadi M.Some notes on the paper"The equivalence of cone metric spaces and metric spaces"[J].Fixed Point Theory and Applications, 2012,87:1~4.
[10]Liu Hao,Xu Shaoyuan.Fixed point theorems of quasicontractions on cone metric spaces with Banach algebras[J]. Abstract and Applied Analysis, 2013, 1~5.
[11]Liu Hao,Xu Shaoyuan.Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings[J]. Fixed Point Theory and Applications,2013,320:1~10.
[12]童裕孙.泛函分析教程 [M].上海:复旦大学出版社, 2003.
AclassofcommonfixedpointtheoremsinconemetricspaceswithBanachalgebras
HUANG Hua-ping1, HU Song-lin1,MING Wei1,ZHOU Hui2
(1. College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China;2. Mathematical Team, Huangshi No.2 Middle School, Huangshi 435003, China)
In this paper, the concept of cone metric space with Banach algebra is introduced, then a class of common fixed point theorems are given. Moreover, an example is used to support the applications.
cone metric space;generalized Lispchitz constant;weakly compatible
2013—10—05
黄华平(1978— ),男,湖北安陆人,讲师,硕士,主要研究方向为函数论.
O177.5
A
1009-2714(2014)01- 0001- 04
10.3969/j.issn.1009-2714.2014.01.001

