两个 Hermite矩阵的组合的特征值的估计

石向前,陈引兰，燕 敏

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

两个 Hermite矩阵的组合的特征值的估计

石向前,陈引兰，燕 敏

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

设A,B是复数域上的两个任意的n阶Hermite 矩阵。讨论了在不同条件下其组合pA+qB+rAB的特征值的估计，其中p,q,r是实数。

Hermite矩阵； 特征值;估计

设A,B是两个n阶Hermite 矩阵，对他们的组合的特征值的估计在实际应用中具有重要的意义。文 [1]给出了Hermite 矩阵的特征值的变分特征以及他们的和的特征值的估计，而文 [2-3]讨论了两个 Hermite矩阵之和的特征值的一些性质，文[4-5] 讨论了两个 Hermite矩阵乘积的特征值的估计。而本文利用A,B的特征值及乘积矩阵AB的特征值来估计组合pA+qB+rAB(其中p,q,r∈)的特征值。为此，先给出几个引理。

引理1[1]设A,B为n阶方阵，则AB与BA有完全相同的特征值。

引理2[2]设A,B是两个n阶Hermite 矩阵，又设诸特征值λk(A),λk(B) ,以及λk(A+B)均按递增顺序λmin=λ1≤λ2≤…≤λn-1≤λn=λmax排列。则对每个k=1,2,…,n, 有

λk(A)+λ1(B)≤λk(A+B)≤λk(A)+λn(B)

引理3[6]设A,B是两个n阶Hermite 矩阵，且A是半正定阵。假设A,B和AB的特征值依升序排列分别是μ1,μ2,…,μn;γ1,γ2,…,γn，λ1,λ2,…,λn则下列各条成立

i)B是半正定，则max{μiγ1,μ1γi}≤λi≤min{μiγn,μnγi},i=1,2,…,n;

ii)B是半负定，则 max{μn-i+1γ1,μnγi}≤λi≤min{μn-i+1γn,μ1γi},i=1,2,…,n;

iii)B是不定，则μn-i+1γ1≤γi≤μiγn,i=1,2,…,n.

引理4[6]设A,B是两个n阶Hermite矩阵，且A,B可交换。假设A,B和AB的特征值依升序排列分别是μ1,μ2,…,μn;γ1,γ2,…,γn和λ1,λ2,…,λn，则

min{μ1γn,μ1γn}≤λi≤max{μ1γ1,μnγn},i=1,2,…,n

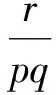
分析易得pA,qB也是两个n阶Hermite矩阵，由引理2，且因为pq≠0，则

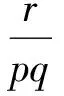
(Ⅰ)

定理1 设A,B是两个n阶Hermite 矩阵，pA是半正定矩阵且AB=BA，假设诸特征值λk(A),λk(B),λk(pA),λk(qB),λk[(pA)(qB)],λk(pA+qB+rAB) (其中p,q,r∈且pq≠0)依升序排列，k=1,2,…，n,若B是半正定的，则

1)当q>0时，有

(1)若r≥0，pq>0,则

pλ1(A)+qλ1(B)+rmax{λk(A)λ1(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λk(A)λn(B),λn(A)λk(B)}

(2)若r≥0，pq<0,则

pλ1(A)+qλ1(B)+rmax{λk(A)λn(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λk(A)λ1(B),λ1(A)λk(B)}

(3)若r<0，pq>0,则

pλ1(A)+qλ1(B)+rmin{λk(A)λn(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λk(A)λ1(B),λ1(A)λk(B)}

(4)若r<0，pq<0,则

pλ1(A)+qλ1(B)+rmin{λk(A)λ1(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λk(A)λn(B),λn(A)λk(B)}

2)当q<0时，有

(1)若r≥0，pq>0,则

pλ1(A)+qλ1(B)+rmax{λn-k+1(A)λ1(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λn-k+1(A)λn(B),λ1(A)λk(B)}

(2)若r≥0，pq<0,则

pλ1(A)+qλ1(B)+rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λn-k+1(A)λ1(B),λn(A)λk(B)}

(3)若r<0，pq<0,则

pλ1(A)+qλ1(B)+rmin{λn-k+1(A)λ1(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}

(4)若r<0，pq<0,则

pλ1(A)+qλ1(B)+rmin{λn-k+1(A)λ1(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}

若B是半负定，则与上述两种情形刚好相反，结论留给读者写出。

1)当q>0 时，qB也是半正定，由引理3可得

max{λk(pA)λ1(qB),λ1(pA)λk(qB)}≤λk[(pA)(qB)]≤min{λk(pA)λn(qB),λn(pA)λk(qB)}

(1)r≥0,pq>0时，有

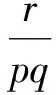
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmax{λk(A)λ1(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λk(A)λn(B),λn(A)λk(B)}

(2)r≥0,pq<0 时，有

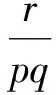
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmax{λk(A)λn(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λk(A)λ1(B),λ1(A)λk(B)}

(3)r<0,pq>0 时，有

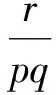
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmin{λk(A)λn(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λk(A)λ1(B),λ1(A)λk(B)}

(4)r<0,pq<0 时，有

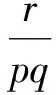
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmin{λk(A)λ1(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λ1(A)λn(B),λn(A)λk(B)}

2)当q<0时，qB是半负定，则由引理3 (ii)可得

max{λn-k+1(A)λ1(B),λn(pA)λk(qB)}≤λk[(pA)(qB)]≤

min{λn-k+1(pA)λn(qB),λ1(pA)λk(qB)}

(1)r≥0,pq>0时，首先有

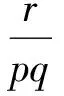
rmin{λn-k+1(A)λn(B),λ1(A)λk(B)}

代入(Ⅰ) 式中就可得

pλ1(A)+qλ1(B)+rmax{λn-k+1(A)λ1(B),λn(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λn-k+1(A)λn(B),λ1(A)λk(B)}

(2)r≥0,pq<0 时，首先有

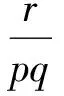
rmin{λn-k+1(A)λ1(B),λn(A),λk(B)}

代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λn-k+1(A)λ1(B),λn(A)λk(B)}

(3)r<0,pq>0 时，首先有

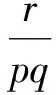
rmax{λn-k+1(A)λ1(B),λn(A)λk(B)}

代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmin{λn-k+1(A)λn(B),λ1(A)λk(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λn-k+1(A)λ1(B),λn(A)λk(B)}

(4)r<0,pq<0时，首先有

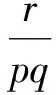
rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}

代入 (Ⅰ)式中就可得到

pλ1(A)+qλ1(B)+rmin{λn-k+1(A)λ1(B),λn(A)λk(B)}≤λk(pA+qB+rAB)

≤pλn(A)+qλn(B)+rmax{λn-k+1(A)λn(B),λ1(A)λk(B)}

定理2 设A,B是两个n阶Hermite 矩阵，AB=BA，pA是半正定阵,B是不定阵,假设诸特征值λk(A),λk(B),λk(pA),λk(qB),λk[(pA)(qB)],λk(pA+qB+rAB) (其中p,q,r∈且pq≠0) )依升序排列，k=1,2,… ，n,则

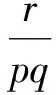
pλ1(A)+qλ1(B)+rλn-k+1(A)λ1(B)≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rλk(A)λn(B)

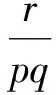
pλ1(A)+qλ1(B)+rλk(A)λn(B)≤

λk(pA+qB+rAB)≤pλn(A)+qλn(B)+rλn-k+1(A)λ1(B)

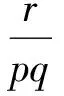
λn-k+1(pA)λ1(qB)≤λk[(pA)(qB)]≤λk(pA)λn(qB)

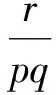
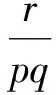
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rλn-k+1(A)λ1(B)≤

λk(pA+qB+rAB)≤pλn(A)+qλn(B)+rλk(A)λn(B)

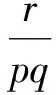
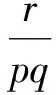
代入(1) 式中就可得到

pλ1(A)+qλ1(B)+rλk(A)λn(B)≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rλn-k+1(A)λ1(B)

定理3 设A,B是两个n阶Hermite 矩阵，AB=BA，若A,B是不定阵。假设诸特征值λk(A),λk(B),λk(pA),λk(qB),λk[(pA)(qB)],λk(pA+qB+rAB) (其中p,q,r∈且pq≠0)依升序排列，k=1,2,……，n,则

1)若r≥0,pq>0时

pλ1(A)+qλ1(B)+rmin{λ1(A)λn(B),λn(A)λ1(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λ1(A)λ1(B),λn(A)λn(B)}

2)若r≥0,pq<0时

pλ1(A)+qλ1(B)+rmin{λ1(A)λn(B),λn(A)λn(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λ1(A)λ1(B),λn(A)λ1(B)}

3)若r<0,pq>0时

pλ1(A)+qλ1(B)+rmax{λ1(A)λ1(B),λn(A)λn(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λ1(A)λn(B),λn(A)λ1(B)}

4)若r<0,pq<0时

pλ1(A)+qλ1(B)+rmax{λ1(A)λn(B),λn(A)λ1(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λ1(A)λ1(B),λn(A)λn(B)}

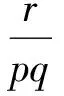
min{λ1(pA)λn(qB),λn(pA)λ1(qB)}≤λk[(pA)(qB)]≤

max{λ1(pA)λ1(qB),λn(pA)λn(qB)}

1)r≥0,pq>0则

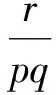
代入(⒈) 式中就可得到

pλ1(A)+qλ1(B)+rmin{λ1(A)λn(B),λn(A)λ1(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λ1(A)λ1(B),λn(A)λn(B)}

2)r≥0,pq<0则

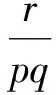
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmin{λ1(A)λ1(B),λn(A)λn(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmax{λ1(A)λn(B),λn(A)λ1(B)}

3)r<0,pq>0则

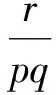
代入(Ⅰ) 式中就可得到

pλ1(A)+qλ1(B)+rmax{λ1(A)λ1(B),λn(A)λn(B)}≤λk(pA+qB+rAB)≤

pλn(A)+qλn(B)+rmin{λ1(A)λn(B),λn(A)λ1(B)}

4)r<0,pq<0则

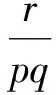
代入(1) 式中就可得到

pλ1(A)+qλ1(B)+rmax{λ1(A)λn(B),λn(A)λ1(B)}≤λk[(pA)+(qB)+rAB]≤

pλn(A)+qλn(B)+rmin{λ1(A)λn(B),λn(A)λn(B)}

上面是考虑A,B二者可交换的情况，而对A,B二者不可交换的情况还尚未解决。

[1]威尔金森 J H.代数特征值问题[M].石钟慈,邓健新,译.北京:科学技术出版社,2001.

[2]合恩 R A,约翰逊 C R.矩阵分析[M].天津:天津大学出版社,1989.

[3]温淑鸿,陈神灿.两个Hermite矩阵之和的特征值的注记[J].福州大学学报(自然科学版),2008,36(6):915～916.

[4]张吉林,杨 晋. 两个Hermite矩阵之和特征值的一些性质[J].太原科技大学学报,2006,27(6):423～425.

[5]唐先华. 两个Hermite矩阵乘积特征值的估计[J].衡阳师专学报(自然科学版),1995,(6):31～37.

[6]徐邦腾.关于两个Hermite矩阵乘积的特征值的估计问题[J].数学的实践与认识, 1995,(2) : 91～94.

TheestimationofeigenvalueofthecombinationoftwoHermitematrix

SHI Xiang-qian,CHEN Yin-lan,YAN Min

(College of Mathematics and Statistic,Hubei Normal University,Huangshi 435002,China)

letA,Bbe two arbitrary order Hermite matrix on complex field. This paper discusses the estimation of the eigenvalues of the combination of pA+qB+tABunder different conditions，andp,q,rare real number.

Hermite matrix; eigenvalue;estimation

2013—11—20

石向前(1987— )，男，湖北红安人，研究方向为代数学.

O151.21

A

1009-2714(2014)03- 0063- 05

10.3969/j.issn.1009-2714.2014.03.015