一类非恰当微分方程的解法

蔡 钢,罗 萍

(重庆师范大学 数学学院, 重庆 401331)

一类非恰当微分方程的解法

蔡 钢,罗 萍

(重庆师范大学 数学学院, 重庆 401331)

讨论一类非恰当微分方程的具体解法, 给出了具体的例子, 完善了一阶微分方程的解法.

微分方程;积分因子;解法

恰当微分方程是微分方程的一个重要部分, 但是很多微分方程都不是恰当微分方程, 因此怎样才能将非恰当微分方法转化为恰当微分方程显得尤为重要. 积分因子的出现, 给我们提供了一种将非恰当微分方法转化为恰当微分方程的途径, 然而要求出一个微分方程的积分因子却不是一件容易的事, 当积分因子为只含x或者y的函数时, 我们可以运用公式很快求出积分因子. 若一个方程含有的积分因子是关于x和y二元函数时, 则要求出积分因子却是一件困难的事. 本文讨论了一类非恰当微分方程, 将它适当分组, 采取分组求积分因子的方法, 求出了这类方程含有x和y的积分因子.

定义1[1]如果方程

P(x,y)dx+Q(x,y)dy=0

(1)

的左端恰好是某个二元函数u(x,y) 的全微分, 即

则称 (1) 为恰当微分方程.

定理2[2]若μ=μ(x,y) 是方程 (1) 的一个积分因子，使得

μP(x,y)dx+μQ(x,y)dy=dΦ(x,y)

则μ(x,y)g(Φ(x,y)) 也是 (1) 的一个积分因子，其中g(·) 是任一可微 (非零) 函数.

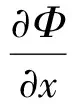
因此

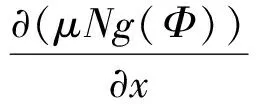
定理3 若μ=μ(x,y) 是方程 (1) 的一个积分因子，即存在Φ(x,y)使得

μP(x,y)dx+μQ(x,y)dy=dΦ(x,y)

(2)

又设μ1=μ1(x,y)为方程 (1) 的另外一个积分因子，即存在Ψ(x,y)

μ1P(x,y)dx+μ1Q(x,y)dy=dΨ(x,y)

(3)

则μ1必可表为μ1=μg(Φ) 的形式，其中g(·) 是任一可微 (非零) 函数.

证明 因为雅克比行列式

所以Ψ和Φ函数相关. 由 (2) 和 (3) 知

现在我们可以给出分组求积分因子法的一般解法. 假设方程 (1) 的左端可以分成两组,即

(P1dx+Q1dy)+(P2dx+Q2dy)=0

其中第一组和第二组各有积分因子μ1和μ2. 从而存在可微函数Φ1和Φ2使得

μ1P1dx+μ1Q1dy=dΦ1,μ2P2dx+μ2Q2dy=dΦ2

由定理2知, 对任意的可微函数h1和h2, 函数μ1h1(Φ1) 是第一组的积分因子，函数μ2h2(Φ2) 是第二组的积分因子. 若能适当的选取h1和h2使得μ1h1(Φ1)=μ2h2(Φ2), 则μ=μ1f1(Φ1) 就是 (1) 的一个积分因子.

下面我们通过具体的例子说明用分组求积分因子法来求微分方程通解的过程.

例1 求解微分方程(x3y+4y2)dx+x4dy=0 .

解 首先将方程左端分成两组:

(x3ydx+x4dy)+4y2dx=0

(4)

观察易知第一组有积分因子x-3和通解xy=C,第二组有积分因子y-2和通解x=C. 我们需要寻找可微函数h1和h2满足

x-3h1(xy)=y-2h2(x)

即是h1(xy)=x3y-2h2(x) . 我们可取h2(x)=x-5和h1(xy)=(xy)-2, 从而方程有积分因子μ=x-5y-2，将它乘在方程 (4) 两端, 得

(xy)-2d(xy)+4x-5dx=0

故通解为 (xy)-1-x-4=C.

例2 求解微分方程ydx-(2x2+2y2+x)dy=0 .

解 首先将方程左端分成两组:

(ydx-xdy)-2(x2+y2)dy=0

(5)

即

解 方程重新分组为

(P(x,y)ydx-dy)+Q(x,y)yndx=0

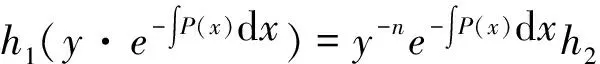
[1]王高雄，周之铭，王寿松,等. 常微分方程(第三版)[M]. 北京: 高等教育出版社，2006.

[2]丁同仁，李承治. 常微分方程教程(第二版)[M]. 北京: 高等教育出版社，2004.

Thesolvingprocessofsomenon-exactdifferentialequation

CAI Gang, LUO Ping

(College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

This paper discusses the solving process of some non-exact differential equation. Some examples are given. We perfect the methods of solution to one order differential equation.

differential equation; integrating factor;solution.

2014—03—18

重庆师范大学基金项目资助(14XLB002)

蔡钢(1984— ),男,重庆巴南区人,讲师,博士生,主要从事泛函分析研究.

O155

A

1009-2714(2014)03- 0109- 03

10.3969/j.issn.1009-2714.2014.03.025