运用灰色系统理论对田径全能项目的分析研究

白 冰

(海南医学院体育部，海南 海口 571101)

运用灰色系统理论对田径全能项目的分析研究

白 冰

(海南医学院体育部，海南 海口 571101)

运用灰色系统理论的关联度分析和优势分析对田径全能运动总成绩与各单项成绩进行分析，找出各个单项与总成绩的关联度，进而分析各个单项中属于优势的项目和属于弱势的项目。为运动员和教练员进行针对性训练提出参考依据。

灰色系统理论;关联度;全能运动;优势分析

1 研究目的

全能运动是一项技术复杂的田径项目。是一项比赛子项多，操作技术强，竞争时间长，跑、跳、投转换快，规则严的高技艺、大强度的综合性田径运动项目。运动员不仅需要有良好的专项训练基础和全面的身体素质水平以及多功能、全方位的熟练的技战术，而且还要具备勇于拼搏、善于竞争的顽强意志品质与瞬息转战的应变能力。虽然全能运动都是由各具体单项组成，但决不等于各个单项的简单相加，它是由具体的单项组合成的一个不可分割的整体性的比赛项目。在比赛中，判定胜负的原则是以运动员参加比赛各项目的累积分，即总分来决定优胜[1，2]。随着全能运动水平的提高，运动员整体实力的增强，在比赛中缺少其中任何一个项目的得分，全能比赛就失去意义。田径全能项目在一定程度上反映了一个国家田径运动的总体水平。目前，对全能运动的研究大部分为全能运动的训练，全能运动员的选材，以及优秀运动员的技术分析。缺少对全能运动各子项之间与总成绩的关系的研究与分析。我们将尝试用灰色系统论对全能运动总成绩与各单项成绩之间的关系进行分析研究。

2 研究方法

2.1 文献资料法

查阅大量与全能运动和灰色系统分析相关的书籍及论文。为课题研究提供理论依据和参考资料。

2.2 数理统计法

利用灰色系统理论中的灰色关联分析对优秀全能运动员的比赛成绩进行处理。

3 研究结果与分析

灰色体统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory),其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度，来判断因素之间关联程度的方法[3，4]。此方法通过对动态过程发展态势的量化分析，完成对系统内时间序列有关统计数据几何关系的比较，求出参考数列与比较数列之间的灰色关联度。与参考数列关联度越大的比较数列，其发展方向和速率与参考数列越接近， 与参考数列的关系越紧密。灰色关联分析方法要求样本容量可以少到4个， 对数据无规律并同样适用， 不会出现量化结果与定性分析结果不符的情况。其基本思想是将评价指标原始观测数进行无量纲化处理， 计算关联系数、关联度以及根据关联度的大小对评价指标进行排序[5，6]。关联度有绝对关联度和相对关联度之分，绝对关联度采用初始点零化法进行处置化处理， 当分析的因素差异较大时， 由于变量间的量纲不一致，往往影响分析，难以得出合理的结果。而相对关联度用相对量进行分析，计算结果仅与序列相对初始点的变化速率有关，与各观测数据大小无关， 这在一定程度上拟补了绝对关联度的缺陷[7，8]。灰色关联度的应用涉及社会科学和自认科学的各个领域。我们将这种方法应用到田径全能项目上。我们选取世界优秀运动员的十项全能成绩(见表1)，把全能成绩作为母因素，各单项成绩作为子因素。运用灰色关联度的方法进行分析。

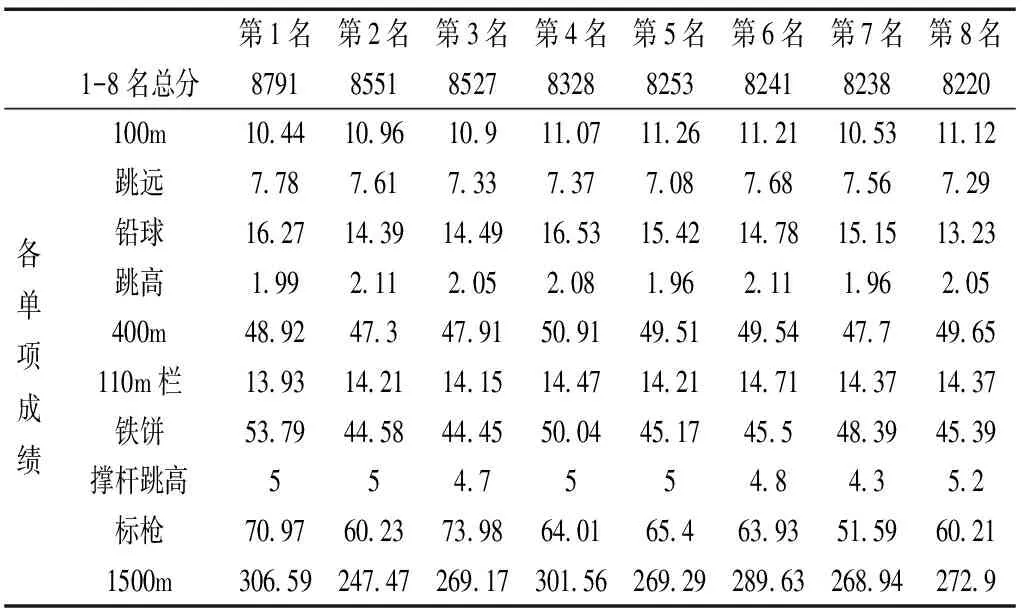
表1 世界优秀十项全能运动员的成绩

3.1 关联度分析计算步骤

3.1.1 确定分析数列

确定反映系统行为特征的参考数列和影响系统行为的比较数列。反映系统行为特征的数据序列，称为参考数列。影响系统行为的因素组成的数据序列 ，称比较数列。针对于全能项目，我们把全能总成绩作为参考数列，把各个单项成绩作为比较数列。

参考数列：Y0(十项全能总分)

比较数列：X1、X2、X3、X4、X5、X6、X7、X8、X9、X10(各单项成绩)。

3.1.2 变量的无量纲化

由于系统中各因素列中的数据可能因量纲不同， 不便于比较或在比较时难以得到正确的结论。 因此在进行灰色关联度分析时，一般都要进行数据的无量纲化处理。

Y0= (1,0.9727,0.9700,0.9473,0.9388,0.9374,0.9371,0.9350);

X1= (1,1.0498,1.0441,1.0603,1.0785,1.0738,1.0086,1.0560);

X2= (1,0.9781,0.9422,0.9473,0.9100,0.9871,0.9717,0.9643);

X3= (1,0.8844,0.8906,1.0160,0.9478,0.9084,0.9312,0.8733);

X4= (1,1.0603,1.0302,1.0452,0.9849,1.0603,0.9849,1.0459);

X5= (1,0.9669,0.9794,1.0407,1.0121,1.0127,0.9751,1.0409);

X6= (1,1.0201,1.0158,1.0388,1.0201,1.0560,1.0316,1.0000);

X7= (1,0.8288,0.8264,0.9303,0.8397,0.8459,0.8996,0.9380);

X8= (1,1.0000,0.9400,1.0000,1.0000,0.9600,0.8600,1.2093);

X9= (1,0.8487,1.0424,0.9019,0.9215,0.9008,0.7269,1.1671);

X10= (1,0.8072,0.8799,0.9836,0.8783,0.9447,0.8772,1.0147).

求两极最小差和两极最大差(标单横线者为最小差,标双横线者为最大差)

Y0与X1

同理：

Y0与X2=(0，0.0054，0.0278，0.0000，0.0288，0.0497，0.0346，0.0292)

Y0与X3=(0，0.0882，0.0794，0.0686，0.0090，0.0290，0.0059，0.0618)

Y0与X4=(0，0.0876，0.0602，0.0979，0.0461，0.1229，0.0478，0.1109)

Y0与X5=(0，0.0058，0.0094，0.0933，0.0733，0.0752，0.0380，0.1058)

Y0与X6=(0，0.0474，0.0458，0.0914，0.0813，0.01186，0.0945，0.0650)

Y0与X7=(0，0.1439，0.1436，0.0170，0.0991，0.0916，0.0375，0.0030)

Y0与X8=(0，0.0273，0.0300，0.0527，0.0612，0.0226，0.0771，0.2743)

Y0与X9=(0，0.1240，0.0724，0.0454，0.0173，0.0366，0.2102，0.2320)

Y0与X10=(0，0.1655，0.0920，0.0363，0.0605，0.0072，0.0599，0.0797)

则总的两级最小差为0，两级最大差为0.2743

3.1.3求关联系数

(∵0.5×0.2743=0.13715)

则Y0与X1关联系数：

即关联度

γ01=(1+0.6401+0.6493+0.5482+0.4953+0.5015+0.6573+0.5313)÷8=0.6279

γ02=(1+0.9618+0.8314+0.9998+0.8266+0.7340+0.7984+0.8243)÷8=0.8720

γ03=(1+0.6058+0.6334+0.6664+0.9387+0.8254+0.9585+0.6894)÷8=0.7900

γ04=(1+0.6102+0.6950+0.5838+0.7483+0.5275+0.7414+0.5530)÷8=0.6824

γ05=(1+0.9593+0.9360+0.5950+0.6518+0.6458+0.7832+0.5644)÷8=0.7669

γ06=(1+0.7432+0.7496+0.6000+0.6278+0.5364+0.5921+0.6786)÷8=0.6909

γ07=(1+0.4880+0.4885+0.8894+0.5806+0.5997+0.7854+0.9789)÷8=0.7263

γ08=(1+0.8340+0.8207+0.7225+0.6915+0.8587+0.6402+0.3334)÷8=0.7376

γ09=(1+0.5251+0.6544+0.7513+0.8881+0.7892+0.3949+0.3715)÷8=0.6718

γ010=(1+0.4531+0.5985+0.7909+0.6940+0.9498+0.6960+0.6325)÷8= 0.7269

关联度大小排序为γ02=0.8720>γ03=0.7900>γ05=0.7669>γ08=0.7376>γ010=0.7269>γ07=0.7263>γ06=0.6909>γ04=0.6824>γ09=0.6718>γ01=0.6279

由此可见，在全能运动中，与总成绩关联程度的大小顺序是：跳远>铅球>400m>撑杆跳高>1500m>铁饼>110m栏>跳高>标枪>100m。

3.2优势分析

优势分析是指在灰色系统理论的关联分析中，多个参考曲线与多个比较曲线构成了一个关联矩阵，通过其矩阵各因素的量化计算，再分辨出众多相关因素的主、次、劣等因素的比较判断过程。亦即是再度将各相关因素相对总体具有何种影响加以排忧的量化比对过程。应用灰色理论中关联分析的原理对全能中各单项对总分的关联度大小排序来决定关联度大者所属项目为优势项，关联度次之者所属项目为次优势项，关联度小者所属项目为非优势项。我们已经通过关联度计算得到了全能运动各单项成绩与全能总成绩的关联度。下面依据关联度大小进行各单项权重总排序。

总关联度(总权重)

∑γi=γ01+γ02+γ03+γ04+γ05+γ06+γ07+γ08+γ09+γ010 =0.6279+0.8720+0.7900+0.6824+0.7669+0.6909+0.7263+0.7376 +0.6718+0.7269=8.4078

通过计算我们得出各单项成绩在总成绩中的权重，那么权重大于0.1的为优势项目，小于0.1的为弱势项目。(见表2)

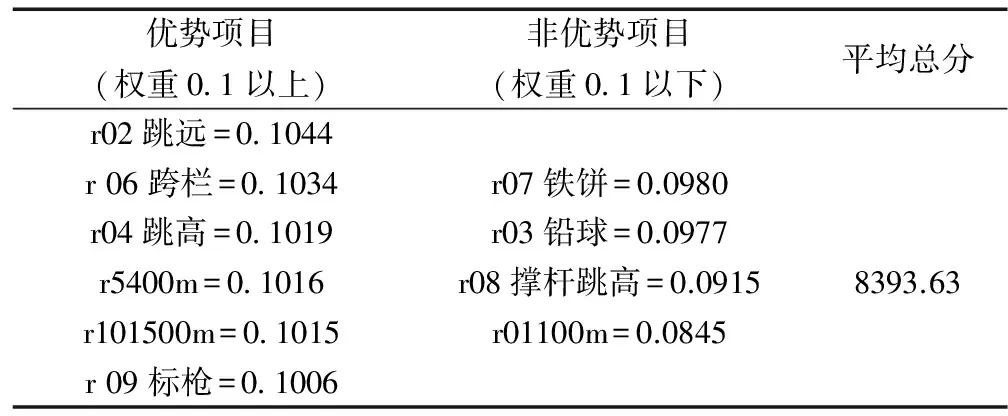
表2 优秀全能运动员总分与单项优势

由表2可以看出，跳远、跨栏为绝对优势项目。说明目前优秀全能运动员在在这两个项目上的技术较为完美。而且优势项目既有径赛项目也有田赛项目，这说明运动员比较注意全面发展。非优势项目中100m为最劣，也就是说运动员在绝对速度上相对来说比较弱，这是全能运动员在今后训练中应注意提高的方面。同样撑杆跳高也属于次最弱势项目，撑杆跳高是田径项目中最为复杂而且难以掌握的项目，对运动员技术技能要求都比较高，要有较高的身体素质才可以很好的掌握此技术活的好成绩。因此，撑杆跳高技术的培养也应该引起全能运动员和教练员的重视。

4 结论与建议

4.1 全能运动员在训练中应有计划、有节奏合理地安排好各子项的训练，各子项将能得到协调的发展，从而提高整体训练效益，获得更好的成绩。

4.2 运动员和教练员要重视绝对速度训练提高100m成绩在总成绩中的权重已达高更高的总成绩。

4.3 加强撑杆跳高技术的训练是提高全能总成绩不可忽视的一个方面。

4.4 通过灰色体统理论分析可以找出全能运动各子项与总成绩的关系，进行比较分析。我们可以运用灰色系统理论的方法进一步分析在训练中各个训练指标对成绩的影响程度，为全能训练提供更好的理论依据。

[1] 文超，等.田径运动训练高级教程[M].北京：人民体育出版社，1994，10

[2] 李远乐，李春雷.对中和世界女子七项全能运动发展特征的研究与分析[J].成都体育学院学报,2001：72-76

[3] 陈志强,杨德芳,黄明教.建立体育多因素聚类的灰色系统回归预测模型方法研究[J].中国体育科技,2001,37(2):13-16

[4] 黄明教.体育实验设计与科学量化方法[M].北京：高等教育出版社，2002：339-344

[5] 徐凤银,朱兴珊,颜其彬,李士伦.储层含油气性定量评价中指标权重的确定方法[J].西南石油学院学报,1994(4)

[6] 安天祥,金志良.中外男子十项全能优秀运动员运动成绩的对比分析[J].沈阳体育学院学报, 2001(2):46-47

[7] 丛湖平.体育统计[M].北京:高等教育出版社,1999：252-266

[8] 李铁录.中外十项全能运动员成绩表现特征的比较分析[J].浙江体育科学,2001(3):47-49

AnalysisofTrackandFieldAll-aroundProjectwithGraySystemTheory

BAI Bing

(Hainan Medical University Sports Department,Haikou 571101,China)

This paper analyses the total score and the individual results of all-round Athletes with gray system theory. It finds out the degree of association of single and total scores, and then analyzes the preponderant and weak projects. The aim of the study is to provide some reference for athletes training.

gray system theory, associate degree, all-around sports, advantage analysis

2013-12-18

白冰(1980-)，辽宁建平人，硕士，讲师

研究方向：网球的教学与训练

G812.6

A

1007-323X(2014)03-0083-04