考虑建站费用的电动汽车充电站选址问题研究

董洁霜，董智杰

(上海理工大学 管理学院，上海 200093)

电动汽车作为一种能源转换效率高、噪声低、零排放的新能源交通工具，正受到人们越来越多的关注。电动汽车充电站的建设是电动汽车普及过程中的关键环节。目前，全国各大城市都加快了充电站的建设步伐以促进新能源汽车的规模化发展。科学地确定充电站的位置及规模，将直接关系到电动汽车用户出行的便捷性和资源配置的合理性，进而影响电动汽车的规模化应用。

近年来，国内外学者对充电站的选址问题展开了大量的研究。针对选址问题的研究主要分为两大类：一类是研究如何满足节点上产生需求的选址问题，如覆盖问题、P-中心问题等；另一类是研究如何满足路径上产生需求的截流选址问题。Kelley等[1](2013)通过对加州南部259位电动汽车驾驶者的调查研究发现电动汽车的充电需求大部分产生于行驶路径而不是产生于某一节点。因此，本文主要对截流选址问题进行综述研究。Hodgson[2](1990)最早提出截流选址的思想并建立了截流选址(FCLM)模型，他认为某些顾客是在事先已经规划好的路径上接受某些服务的，如上下班通勤过程中接受银行ATM机、加油站或便利店服务等。FCLM模型的目标是确定P个服务站的选址使得至少通过服务站一次的客流量总和最大。杨珺[3-5]等在FCLM的基础上研究了带容量限制及偏离最短路径条件下的扩展模型并给出了启发式算法。Hodgson的截流选址模型中假定一条路径上只要设有一个服务站，则该条路径上的所有流量都能被服务。但是，由于电动汽车续航里程的限制，完成一次长距离的出行往往需要接受多次充电服务，因此，FCLM模型中的这个假定条件在充电站选址问题上显然不成立。为了解决该问题，Kuby和Lim[6]在FCLM模型的基础上建立了FRLM模型，提出了“充电站组合”的概念，顾客通过路径上的若干个充电站可以完成一次出行。该模型的目标同样是确定P个服务站的选址使得完成出行的客流量最大。但是FRLM模型的求解需要两个步骤。首先需要列出每条路径上所有可行的充电站组合。然后将可行的充电站组合输入模型，用贪婪算法进行求解。由于列出充电站组合是一项十分耗时的过程，不适用于求解大型问题。Lim和Kuby[7](2010)提出了求解FRLM模型的启发式算法。Caper和Kuby[8](2012)提出了另一种一步解决FRLM的方法，他们在FRLM模型中新增了3个约束以确定路径上设置的充电站能够使顾客完成一次出行。

以上的充电站选址模型都是用于求解最大覆盖问题的。Wang[9](2007)首先提出了基于最小集合覆盖思想的充电桩选址模型。每个充电桩单次可以满足一辆电动汽车的充电需求。该模型规定了总充电时间的下限α，以保证电动汽车可以完成一次出行。其目标是在满足服务需求的前提下，确定每个候选点的充电桩数量使得总建站费用最小。然而该模型仅考虑了单条路径的充电站选址行为。但实际上，路网中会有从不同起点出发沿着不同路径到达不同讫点的车流。因此，Wang[10](2011)在此基础上建立了多路径的充电站选址模型并考虑了实际情况中的充电效率及充电时间对充电桩选址及数量的影响。

在以往求最小建站费用的模型中，候选点的建站费用都是事先确定的常量，而没有深入的考虑影响建站费用的因素。但在实际情况中，充电站的建站费用与其所含充电桩的数量息息相关。Wang的模型中，候选点充电设施的建设费用与其所布设的充电桩数量呈线性关系。然而，在充电桩的建设过程中，还涉及到不同程度的配套设施建设和电网改造费用。因此，充电站的建站费用与其所含充电桩的数量应当呈非线性关系。本文考虑了建站费用与其所含充电桩数量的关系，并将这种关系引入选址模型，提出了考虑建站费用的充电站选址模型，并通过上海市崇明县的算例，对比了三种不同关系参数下选址结果的差异，验证了考虑建站费用的充电选址模型与传统选址模型在选址结果上的差异。

1 模型的建立

Wang(2011)基于最小集合覆盖思想建立了充电桩选址模型，并以澎湖列岛为例确定了旅游线路上每个候选点的充电桩个数。该模型考虑了充电效率和充电时长的因素。电动汽车在充电站的充电时长取决于其剩余电量及充电桩的充电效率。电动汽车在某点的剩余电量等于其在上一点的剩余电量减去在两点之间行驶消耗的电量，且最长的充电时间不超过在充电站的停留时间，当电池充满后，就不再进行充电。Wang假定每个充电站的建设费用与其所含充电桩的数量呈线性关系。但实际上，充电站的建设费用与充电桩的数量可能存在以下三种关系：①建设每个充电桩都需要配置相应的基础设施。充电桩的数量越多，则基础设施的配置费用越低，单个充电桩的建设费用越小。此时，充电站建设费用除以充电桩数量的值逐渐变小。②与Wang的假定相同，充电站的建设费用与其所含充电桩的个数呈线性关系。③建设每个充电桩都需要进行相应的电网改造。充电桩的数量越多，则电网改造的难度越大，单个充电桩的电网改造费用越大。此时，充电站建设费用除以充电桩数量的值逐渐变大。因此，本节中建立的充电桩选址模型在Wang(2011)模型的基础上考虑了充电站建设费用与充电站所含充电桩数量的关系，模型中涉及到的符号如下所示：

(1)标示。m为第m辆电动汽车；i，j为节点或候选点。

(2)集合。M为电动汽车集合；N为点集合；A为路段集合。

(3)模型参数。fi为在候选点i的建站费用；e为充电站的充电效率(单位分钟充电所增加的行驶距离(km/min)；dij为点i和点j之间的距离；γ为电池的最大充电状态，即电动车满电情况下可以行驶的里程；ui为i点可容纳的最大充电桩数；ti为停留时间，即车辆m在i点的最长充电时间；αi为i点的关系模型待定参数；βi为i点的关系模型待定参数；δijm为若第m辆电动车的行驶路径上包含路段ij，则δijm=1，否则δijm=0。

(4)决策变量。rmi为第m辆电动汽车在i点充电后所增加的行驶里程；xi为i点的充电桩数量，xi>=0；ymi为若电动汽车m在i点充电，则ymi=1，否则ymi=0；bmi为第m辆电动汽车在i点所拥有的剩余电量可供其行驶的里程。

利用这些符号，充电站的定容选址问题可以建模如下：

目标函数为：

。

(1)

约束条件为：

bmj=(bmi+rmi)-dij·δijm∀ij∈A∀m∈M。

(2)

rmi≤γ-bmi∀i∈N∀m∈M。

(3)

rmi≤ymitmie∀i∈N∀m∈M。

(4)

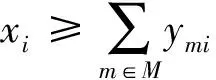
(5)

xi≤ui∀i∈N。

(6)

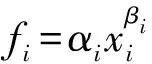
(7)

ymi∈(0,1) ∀i∈N∀m∈M。

(8)

xi,bmi,rmi≥0 ∀i∈N∀m∈M。

(9)

其中，公式(1)表示求最小建站费用。公式(2)表示电动汽车从i点行驶至j点，其在j点的剩余行驶距离等于在i点的剩余行驶距离加上在i点充电后所增加的行驶距离再减去i、j之间的距离。公式(3)表示电动汽车在i点可充入的最大电量不超过已消耗的电量。公式(4)表示电动汽车在i点可补充的最大电量不超过其在停留时间内，以速率e充入的电量。公式(5)表示i点的充电桩数量不少于在i点充电的车辆数。公式(6)表示i点的充电桩数量不超过其限定的最大容量。公式(7)表示充电站建设费用与充电桩数量的关系式。公式(8)表示决策变量ymi为0，1变量。公式(9)表示决策变量xi，bmi，rmi非负。

公式(7)假定充电站的建设费用与充电站所建充电桩的数量呈幂函数关系，当β=1时，即表示充电站的建站费用与其所含的充电桩数量呈线性关系。此时，本文中所提出的模型与不考虑建站费用的传统充电站选址模型一致。当β<1时，单个充电桩的建设费用随着充电站规模的扩大而逐渐降低。当β>1时，单个充电桩的建设费用随着充电站规模的扩大而逐渐升高。

2 算例分析

为了进一步分析建站费用对充电站选址结果的影响，给出一个简单的算例进行验证说明。由于本文中所提出的选址模型是一个混合整数规划，所以使用lingo软件中比较成熟的分支界定法进行求解。

以上海市崇明县为例，崇明岛地处长江口，是中国的第三大岛，岛上自然风光秀美，拥有东滩湿地，东平国家森林公园等著名景点。“生态”，“环保”亦是崇明规划和建设的主题词，随着崇启大桥和长江隧桥的建成通车，崇明未来每年将吸引超过400万人次的游客来岛上观光旅游。为了发展崇明的旅游产业，保护崇明的生态环境，推广电动汽车是一项十分有效的举措。

普通加油站通常布设在交通干道的沿线或车辆汇集较多的地方，车辆加油时间较短。但是电动汽车的充电时间与充电站的充电效率息息相关，慢速充电桩的充电效率较低，充电时间较长。Wang(2011)提出，充电站宜布设在靠近旅游景点的地方，用户在充电的同时可以参观旅游景点。其实，用户在充电的同时，也可以进行一些其他的活动，例如旅游参观，购物，饮食，休闲娱乐等。因此，在交通吸引点的附近也可以布设充电站。

如图1所示是崇明县的热门旅游线路及其周边的旅游景点和重要集镇。将其简化，沿线在靠近景点，重要集镇和娱乐休闲设施附近共设置13个候选点。旅游环线总长为142.2 km，目前崇明县域内仅在陈家镇设立有一个电动汽车充电站，而在一些重要的旅游集散点，如森林公园，东滩湿地等尚未设立充电站。电动汽车的蓄电池大多采用铅-酸蓄电池，一般只适用于短途出行(充满电大约能续航50 km)。对于崇明县总长为142.2 km的旅游线路，假设出发时的电量为满电，则至少需要充电两次才能环绕全线。因此，加大充电站的覆盖密度，是解决电动汽车出行限制的有效对策。

根据实际情况，给出了出行者在各候选点的平均停留时间ti见表1。

图1 崇明县旅游线路

表1 候选点停留时间表

由表1中数据可知，由于充电桩充电速度的局限性，充电汽车在充电站的平均停留时间不一定能满足充电汽车的充电需求，假设充电桩的充电效率为(0.208 km/min)则其在A点的停留时间内，最长能够新增的续航里程为20.8(0.208×100)km，不到其电池容量50 km的一半。因此，用户若需要完成一次长距离的出行，必须经过多次充电。根据现有资料，崇明县几条主要出行线路的出行分布情况见表2：

表2 主要出行线路出行分布表

表2中，仅线路1，2，6的长度低于电动汽车的最大续航里程50 km，其余几条线路的长度均超过了电动汽车的最大续航里程，均需要接受至少一次的充电服务才能完成出行。

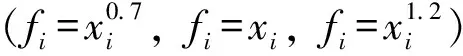
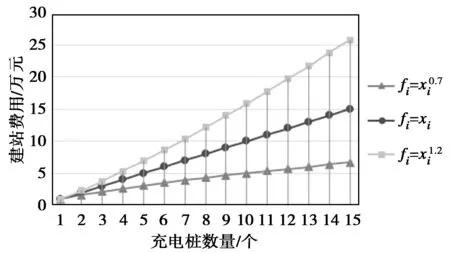
图2 不同参数下建站费用与充电桩数量关系

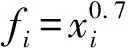
表3 不同容量及参数设定下充电站选址结果

3 结束语

本文考虑建站费用与充电桩数量的关系，建立了函数关系模型，并在此基础上提出了充电站选址模型。通过算例，对比了三种不同关系模型参数下选址结果的差异，验证了建站费用对选址行为的影响。然而，本模型在参数α，β的标定上，仍然没有足够的实际数据作为支撑。文中所提出的模型假设所有电动汽车的充电需求都能被满足。但是实际情况中，由于财政预算和资源的限制，充电站的建设不可能满足所有电动车的充电需求，因此建立基于最大覆盖思想的选址模型也是很有必要的。

【参 考 文 献】

[1]Kelly S，Kuby M.One the way or around the corner Observed refueling choices of alternative-fuel drivers in Southern California[J].Journal of Transport Geography，2013，33：258-267.

[2]Hodgson J.A Flow-capturing location allocation model[J].Geographical Analysis，1990，22(3)：270-279.

[3]杨 珺.一类带服务半径的服务站截流选址-分配问题[J].系统工程理论与实践，2006(1)：117-122.

[4]杨 超.一类带容量限制的服务站选址问题[J].系统工程，2004，22(1)：19-23.

[5]杨 珺.需求不确定情况下的服务站截流选址分配问题研究[J].物流技术，2005(8)：50-53.

[6]Kuby M，Lim S.The flow-refueling location problem for alternative-fuel vehicles[J].Socio-Economic Planning Sciences，2005，39(2)：125-145.

[7]Lim S，Kuby M.Heuristic algorithms for siting alternative-fuel stations using the flow-refueling location model[J].Eur J Oper Res，2010，204(1)：51-61.

[8]Caper I，Kuby M.An efficient formulation of the flow refueling location model for alternative-fuel stations[J].IIE Transactions，2012，44(8)：622-636.

[9]Wang Y.An optimal location choice model for recreation-oriented scooter recharge stations[J].Transportation Research Part D：Transport and Environment，2007，12(3)：231-237.

[10]Wang Y.Locating flow-recharging stations at tourist destinations to serve recreational travelers[J].International Journal of Sustainable Transportation，2011，5(3)：153-171.