基于k-mean聚类与灰度梯度最大熵的树木图像分割
白雪冰,陈 凯,郭景秋,祝 贺,张庭亮
(东北林业大学 机电工程学院,哈尔滨 150040)
自20世纪开始,计算机技术得到了长足的进步,数字图像处理也随之快速的发展起来。数字图像处理就是利用计算机或其他数字硬件,对从图像信息转换而得的电信号进行某些数学运算,以提高图像的实用性[1-3]。目前数字图像处理所处理的图像信息大多数是二维信息,所以信息量很大,加大了图像处理的难度,因此也对计算机会有较高的要求,如存储容量和计算速度等。由于数字图像中各个像素点之间具有较大的相关性与不独立性,所以,图像处理中能够具有较快的处理速度和精度与图像信息的压缩还有很大的发展空间[4-6]。
本文结合目前的彩色图像处理算法提出了基于k-mean聚类与灰度-梯度最大熵的树木图像分割算法,该算法为了更好地区分目标图像与背景,先采用k-mean聚类初分割,再利用灰度-梯度空间能够明确的描述图像中各像素点灰度与梯度的分布规律及图像中的所需目标图像与背景之间的边缘情况[7],基于灰度-梯度最大熵进行精分割,因此,图像分割所得到的结果将更为理想,精度得到一定提高,处理速度也有所提高。
1 k-mean聚类初分割
k-means算法是一种经典的基于距离的算法,用距离的远近来评价其相似性,即认为两个对象距离越远,相似性就越小,而距离越近,其相似度就越大,因此该算法最终得到紧凑且独立的簇。
算法过程如下:
(1)从整体N个类别中任意选出K个类别作为聚类中心。
(2)对其他的每个类别计算其到每个聚类中心的距离,并把该类别归为最近的聚类中心的类。
(3)再重新计算已经分出的每一个类的聚类中心。
(4)迭代(2)~(3)步直至新的中心与原中心相等或小于指定阈值,算法结束。
K-mean聚类算法将对象分为K个类别C={ck,i=1,2,…,K}每类含ck有一个聚类中心μi,应用欧式距离公式计算类内各点到聚类中心μi的距离平方和:
。
(1)

图1 K-mean聚类初分割
从图中看出,图像被分别聚成了两类,三类和四类。聚成三类或者四类的时候,出现了目标和背景区域混淆的情况,效果较差。图1中原图是一副背景简单的树木图像,聚成两类比较合适。
2 灰度-梯度最大熵算法
2.1 灰度-梯度共生矩阵
描述图像的过程中,将灰度分布与梯度信息融合得灰度梯度共生矩阵[2](GGCM),设一幅M×N灰度图像f(m,n);m=0,1…M-1,n=0,1,…N-1,则灰度归一化图像和梯度归一化图像分别为:
(2)
(3)
式中:Lf为最大灰度级;Lg为最大梯度级;fmax为灰度矩阵最大值;gmax为梯度矩阵最大值[4]。
GGCM定义为H=(hxy),x=0,…,Lf-1,y=0,…,Lg-1,其中元素H(x,y)定为F(m,n)与G(m,n)中具有灰度级x和梯度级y的像点数,归一化图像为:
(4)
2.2 灰度-梯度最大熵
共生矩阵是Lf×Lg维的矩阵的图像,设(Lf-1)×(Lg-1)大小的区域为图像的二维直方图,如图2所示,共生矩阵坐标系的原点在左上角,其中横坐标为图像的梯度值且横向递增,纵坐标为其灰度值且纵向递增。定义阈值在(s,t),由于阀值处灰度值与梯度值区分明显,目标的灰度值较低而背景的灰度值较高,所以共生矩阵就被分为A、B、C、D四个象限。本算法是以灰度-梯度共生矩阵和最大熵基础,充分结合了图像的灰度和梯度信息。
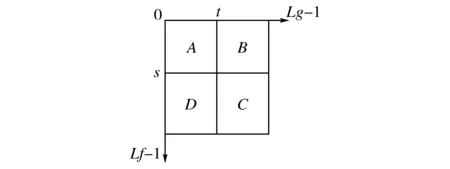
图2 共生矩阵四个区域
物体和背景的灰度值变化不大,所以灰度值比较小:A(0≤i≤s,0≤j≤t)表示物体,D(s+1≤i≤Lf-1,0≤j≤t)表示背景。随着t值不断变大,其对应像素点是目标与背景边界的概率增加,因此共生矩阵在B(0≤i≤s,t+1≤j≤Lg-1)中的元素kij为灰度i属于物体和梯度j属于边缘转移数目,在C(s+1≤i≤Lf-1,t+1≤i≤Lg-1)中元素的kij为灰度i属于背景和梯度j属于边缘数目,所以4个象限像素和为:
(5)
将pij正规化为:
(6)
由此可知其条件熵为:
(7)
(8)
所以图像的条件熵为:
(9)
依据最大熵理论,H获得最大值的(s*,t*)即是最佳阈值[6]:
(10)
最后对灰度-梯度最大熵的分割结果进行形态学后处理,通过标注连通对象,计算标注的面积,去除面积比较小的部分,可以实现对背景非目标区域信息比较理想的清除,再通过膨胀操作将图像边缘中的薄弱断开处进行连接,通过腐蚀操作将粘连的目标部分断开。从分割结果看出,获得了完整的闭合曲线轮廓。
3 实验结果
基于以上理论基础,应用计算机,Matla7.0集成环境[11-13]对树木图像进行分割,分割过程及其结果分析如图3所示。

图3 实验结果
对经过灰度-梯度最大熵方法的分割后结果进行形态学后处理操作,从分割结果看出,获得了完整的闭合曲线轮廓,获得更多的树木边缘信息,细节处分割效果较好,对于树木中的明显空洞也分割的较为清晰[6],分割时间为t=102 407.000us。
应用灰度-梯度最大熵对不同图像分割结果如图4所示。

图4 不同背景下树木图像分割
从分割结果看出,获得了完整的闭合曲线轮廓,细节处分割效果较好,对于树木中的明显空洞也分割的较为清晰,整个分割过程运行时间可以接受,但是在聚类过程可能会尝试几次确定合适的类数,导致分割具有一定程度的复杂性[5]。
二维最大熵与灰度-梯度最大熵分割结果对比如图5~图7所示。

图5 样本一

图6 样本二

图7 样本三
两种分割方法运行时间对比见表1。
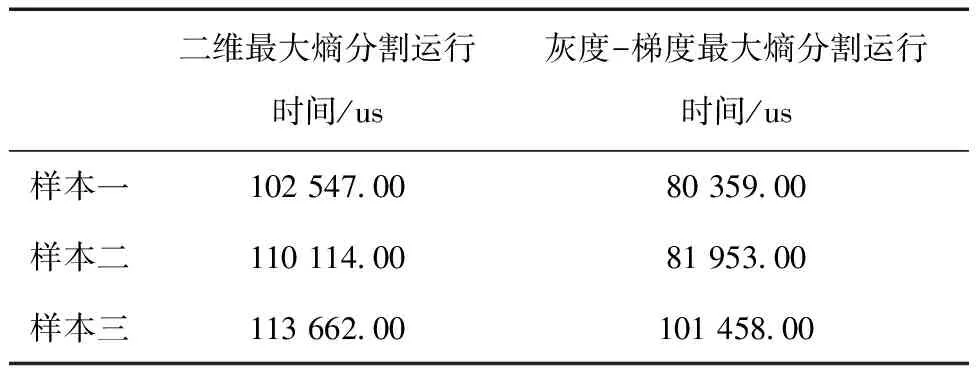
表1 两种分割方法运行时间对比
将之前的分析结果结合表格1可以直观的看出,对于树木图像分割,灰度-梯度最大熵分割结果的分割效果要好于二维最大熵分割结果[7]的分割效果,且运行时间明显小于其运行时间。结合上述各组实验的结果图像的分析可知,灰度-梯度最大熵分割结果可以分割出较为完整的闭合曲线,因为结合了图像的梯度信息,所以可以获得较好的边缘轮廓线。
4 结束语
该算法对彩色树木图像的分割具有较好的分割效果。对于背景比较复杂的树木图像,运用基于k-mean聚类与灰度-梯度最大熵算法的分割算法对图像进行分割,可以获得较完整的闭合曲线,效果较好,再通过形态学后处理可以消除背景非目标区域的干扰,且程序运行速度较快,精度较高。当然这种方法也存在缺点,对于树木中的空洞繁多,基于k-mean聚类与灰度梯度最大熵算法分割获得的图像边缘和原图像边缘会有出入,这样就可能丢失了部分的树木信息。
【参 考 文 献】
[1]王克奇,马晓明,白雪冰.基于分形理论和数学形态学的木材表面缺陷识别的图像处理[J].森林工程,2013,29(3):48-50+53.
[2]梁 建.基于灰度-梯度共生矩阵的植被提取方法[J].海洋测绘,2013,33(1):29-31.
[3]朱 峰,王海丰,任洪娥.基于Gabo变换的纹理图像分割算法及应用[J].森林工程,2013,29(5):60-63.
[4]郭 烈,王荣本,金立生,等.基于二维最大熵阈值分割的坑识别方法[J].计算机工程与应用,2006(21):226-228.
[5]王晓松.复杂背景下树木图像提取研究[D].北京:北京林业大学,2010.
[6]蔡世捷.基于Matlab的树木图像分割方法研究[D].南京:南京林业大学,2005.
[7]洪继光.灰度-梯度共生矩阵纹理分析方法[J].自动化学报,1984,10(1):22-25.
[8]周德龙,申石磊.基于灰度-梯度共生矩阵模型的最大熵阈值处理算法[J].小型微型计算机系统,2002,23(2):136-138.
[9]陈 果,左洪福.图像分割的二维最大熵遗传算法明[J].计算机辅助与图形算法,2006,14(6):530-533.
[10]王再尚.Markov随机场的树木表面缺陷模式识别方法的研究[D].哈尔滨:东北林业大学,2012.
[11]蒋庆丰.K-Means聚类算法研究及图形演示的实现[J].信息技术,2010,10(3):22-25.
[12]阚江明,李文彬.基于数学形态学的树木图像分割方法[J].北京林业大学学报,2006,40(S2):12-30.
[13]季 虎,孙即祥,邵晓芳,等.图像边缘提取方法及展[J].计算机工程与应用,2004,40(14):70-73.

