基于分支定界法甩挂运输站场选址研究

王尔媚，马成林，李慧子，王秋霏，周 沫，张一珠

(东北林业大学 工程技术学院，哈尔滨 150040)

中国经济的快速发展和人民物质需求的日益增长，为物流行业提供了广阔的市场。但是整个物流运输业也面临着前所未有的挑战，劳动力成本上升、专业人才匮乏、信息系统的不完善以及低碳物流的兴起都给物流企业带来了冲击[1]。在这个机遇与挑战并存的环境下，甩挂运输作为一种节能减排、低碳高效的运输方式，在国家的大力倡导下，受到越来越多物流企业的青睐。

在全国范围内开展甩挂运输，选址分配是一个重要环节，在整个物流系统中起着承上启下的作用，其目标是促进货运运输向组织化、综合化、合理化和现代化的方向发展[2]。目前，关于选址问题的研究大部分考虑的是针对传统运输模式下的物流配送中心选址问题进行研究，M.T.Melo等人提出了多期选址模型，用来结局参数可以预测的方式随时间变化的情况[3]。A.Klose将选址模型由单一产品模型扩展为多产品模型[4]。孙会君，高自友从系统的角度研究了配送设施的选址规划。对于不同的选址模型，传统的研究方法主要有整数规划法、图上作业法、重心法以及仿真方法等，也有许多新的方法例如遗传算法、模拟退火法以及蚁群算法等等[5]。陈曦、傅明在《GIS环境下的物流配送中心选址模型与算法研究》一文中采用了遗传算法对选址问题进行研究。但是目前针对甩挂运输站场选址的研究很少，本文针对多产品供应链网络对甩挂运输站场的选址问题进行研究，建立了一个两阶段多产品甩挂站场的选址及用户分配模型[6-7]，并采用分支定界法[8]借助Matlab对所建立的模型进行求解[9-11]。

1 选址模型的建立

1.1 模型描述

本文选取某汽车物流公司整车运输网络为实例进行分析。已知该公司的整车运输遵循“两级分拨发运”体系。即：各生产基地的成品整车由整车分拨中心(VDC)运至各整车仓储中心(VSC)，然后交付于授权经销商或直销客户，如因业务需要，也会考虑由VDC直接发运至经销商或直销客户，如图1所示。

针对该公司的实际情况，考虑涉及多阶段选址的多产品供应链网络优化问题。由于主机厂与VDC距离很近且一一对应，故将整车分拨中心视为工厂，将中转库或直销商视为用户，经过甩挂站场完成供需环节。由于甩挂站场也可能是用户或者工厂，所以这里包括由工厂直接为用户供货的情况。

图1 某公司整车物流业务模式

1.2 模型的基本假设

模型的基本假设如下：

(1)由于同一工厂不同品牌的车可以拼装，所以不考虑品牌因素，认为一个工厂生产的是同一种产品。

(2)甩挂站场选择租用的形式，认为每个甩挂站场的容量已知且能够满足需求。其固定租用费用已知。

(3)工厂对每个用户均有供货。每个用户对各个工厂的产品均有需求。

(4)工厂生产的产能已知，各用户对不同产品的需求已知。

(5)工厂的生产总量等于用户的需求总量。即供需平衡。

1.3 模型及其意义

针对上述实例，建立一个基于“工厂—甩挂站场—用户”两阶段多产品甩挂站场的选址及用户分配模型。目标函数是包括运输成本，甩挂站场的租用成本及产品管理成本在内的总成本最低。具体数学模型如下：

(1)

S.t.

(2)

(3)

(4)

(5)

i=1,2,……,a,j=1,2,……,b,k=1,2,……,c。

式中：a为工厂的个数及产品的种数；b为甩挂站场的个数；c为用户的个数；Wij为工厂i是否为甩挂站场j提供产品i，提供为1，反之为0；Cij为工厂i到甩挂站场j的单位运价，单位：万元；Xij为工厂i到甩挂站场j的运量，单位：辆；Sjki为甩挂站场j是否为用户k提供产品i的单位运价，单位：万元；Yjki为甩挂站场j为用户k提供产品i的量，单位：辆；Bj为甩挂站场j是否被选中；Ei为甩挂站场j的租赁费用，单位：万元；Ui为甩挂站场j的单位产品管理费用，单位：万元；Wi为工厂i生产的产品i的量，单位：辆；Gj为甩挂站场j的容量，单位：辆；Hki为用户k对产品i的需求量，单位：辆。

2 模型的求解

2.1 分支定界法

分支定界(branch and bound)算法是一种在问题的解空间树上搜索问题的解的方法，采用广度优先或最小耗费优先的方法搜索解空间树。在分支定界算法中，每一个活结点只有一次机会成为扩展结点。

利用分支定界算法对问题的解空间树进行搜索，它的搜索策略是：

(1)产生当前扩展结点的所有子结点。

(2)在产生的子结点中，抛弃那些不可能产生可行解(或最优解)的结点。

(3)将其余的子结点加入活结点表。

(4)从活结点表中选择下一个活结点作为新的扩展结点。

如此循环，直到找到问题的可行解(最优解)或活结点表为空。

2.2 利用Matlab求解步骤

为了得到上述模型的解，采用分支定界法进行计算并借助Matlab工具箱运行计算过程。在Matlab中对整数规划模型进行编程，调用Matlab的自嵌函数Bintprog，通过分支定界法对该模型进行求解。主要步骤如下：

(1)计算工厂到甩挂站场的费用，得到矩阵A。

(2)计算甩挂站场到用户的费用，得到矩阵B。

(3)甩挂站场的建设费用设为矩阵C。

(4)设置变量Xijk表示工厂i是否通过甩挂站场j给用户k运送货物，X∈{0，1}，得到的矩阵记为X。假设有m个工厂n个用户，则共有m×n条路径，每条路径有l个甩挂站场可供选择，则X为一个m×n×l的矩阵。

(5)设置变量Yj甩挂站场j是否需要建设，Yj∈{0，1}，得到的矩阵记为Y。因为甩挂站场j是否建设决定于有无路径通过该处，与通过的次数无关，故Y为1×l的矩阵。

(6)目标函数变为：minZ=AX+BX+CY，由于工厂到用户的路径是唯一且连续的，即工厂—甩挂站场—用户模式，故A对应的X与B对应的X为同一矩阵，所以目标函数可以合并为minZ=(A+B)X+CY。

(7)约束变量公式为：

(7)

(8)

k=1,2,......,b。

(9)

(8)编写程序代码，调用函数bintprog，利用分支定界法对模型求解。

3 实例分析

3.1 实例数据

已知该汽车物流公司的整车物流运作流程图如图1所示，在全国范围内有7个工厂，对应图1中的VDC，有37个用户，对应图1中的VSC及经销商。现欲从11个甩挂站场候选地中选择合适的地点建立甩挂运输站场。为了对模型进行求解，需要已知以下数据：工厂的生产量及各用户对工厂的需求量，工厂到甩挂候选站场的单位运价和距离，甩挂候选站场到用户的单位运价和距离，甩挂候选中心，固定投资费用及建设容量，分别见表1～表7。

表1 工厂生产各产品的量 辆

表2工厂的供货量以及各用户对各工厂的需求量辆

Tab.2 Factory shipments and users’demand of each plant vehicles

工 厂小 计沈 阳南 京上 海烟 台青 岛柳 州仪 征北 京45287706877882340天 津418103666656812224沈 阳8274775011855444042南 京4 6363001 167992483613265815上 海2 3301262811 283143158138201烟 台2 244203194568601440103134青 岛2 244174355566434481103131成 都1 928148391310196282381220重 庆64845124109607015584郑 州9918925615511015748174武 汉5673915411056635590哈尔滨25074313335461119长 春445123606272721938营 口496230697046312128石家庄9072111271281521524195呼和浩特49289737294942249太 原389386453771021838晋 中38945515779912047西 安490361088359783295咸 阳29421564838691942济 南2 244180375464448519106151银 川1751829243540821兰 州27021584138541543杭 州2 414162526763257284140281

续表2工厂的供货量以及各用户对各工厂的需求量辆

Tab.2 Factory shipments and users’demand of each plant vehicles

工 厂小 计沈 阳南 京上 海烟 台青 岛柳 州仪 征南 昌4943511210648545187长 沙60042117104576413087昆 明5994198114536515870贵 阳21914383620236127福 州5724512014866664878拉萨424777728乌鲁木齐38629835953762164合 肥63041159132687132128广 州1 43497243282130160341180东 莞86063181158787920199南 宁25617404223267929海 口1068191810103011西 宁21517503927261343合 计32 9533 4956 0027 4884 3434 8362 9753 814

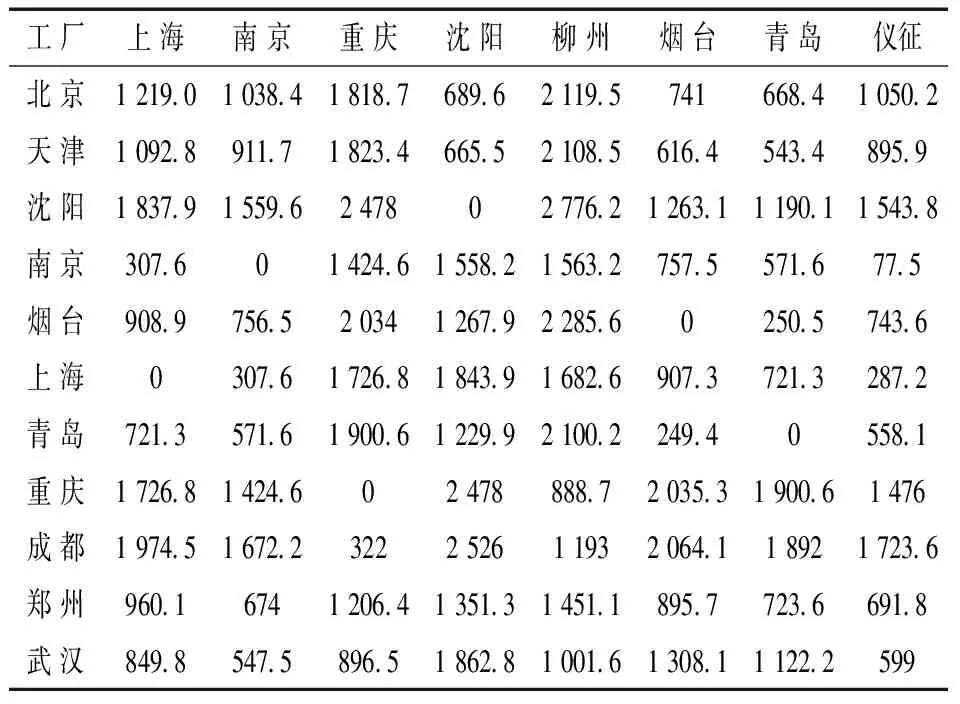
表3 工厂到甩挂站场候选集的距离 km

表4 从工厂到甩挂站场候选集的单位运价 元

表5 甩挂站场候选集到用户的距离 km

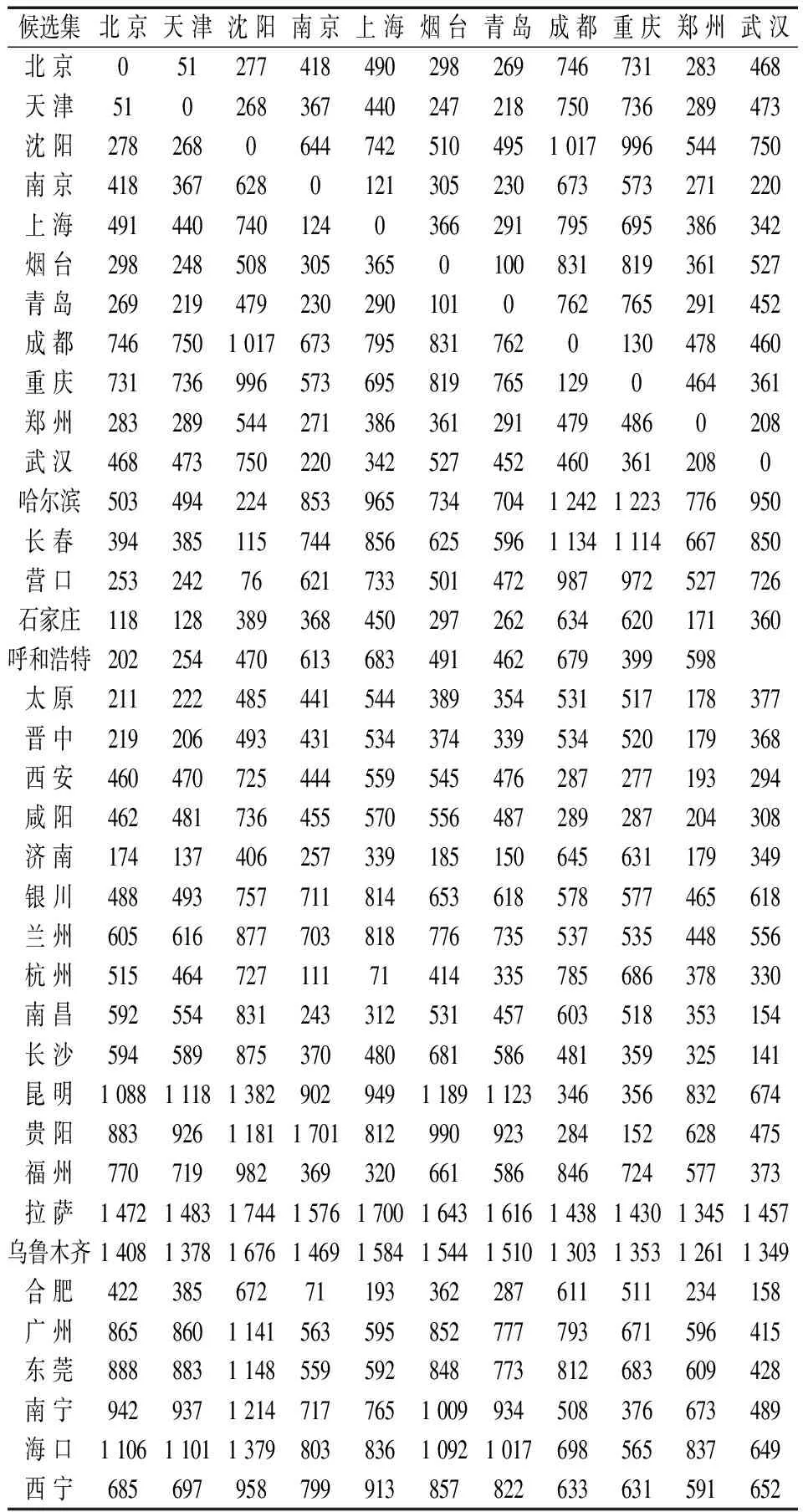
表6 甩挂站场候选集到用户的单位运价 元

表7 甩挂候选站场的固定投资费用及建设容量

3.2 模型求解

根据本文2.2所示求解步骤进行求解。其中，m为7，n为37，l为11，故X为一个259×11的矩阵，Y为1×11的矩阵。依模型的求解步骤程序进行求解，得到结果见表8。其中Ji等于0表示甩挂候选站场i未被选中，Ji等于1表示甩挂候选站场i被选中。

表8 甩挂候选站场求解结果

最终从11个甩挂候选站场中选择了8个，作为该公司开展整车甩挂运输的中转站场。

4 结束语

甩挂运输站场的选址与其他物流中心的选址比较，具有其特殊性。本文将传统的物流选址理论及方法与甩挂运输的特点相结合，在解决甩挂运输站场选址问题时，以某汽车物流公司整车运输网络为研究原型，考虑了多产品两阶段甩挂运输的供应链网络结构，建立了以总成本最小为目标的整数规划模型，将甩挂运输站场的选址与上游供应商和下游用户相互依存，使选址结果更加合理，降低了甩挂运输成本，为社会带来环境效益的同时也为企业带来经济效益。采用分支定界法并借助Matlab工具箱对整数规划模型进行求解，既保证了结果的合理性，又有效的简化了运算的复杂程度。

【参 考 文 献】

[1]吴 宇，曾传华，杨 伟.道路运输组织甩挂运输策略研究[J].物流工程与管理，2010(8)：83-85.

[2]Andre L,Diane R.Logistics systems design and optimization[M].New York:Springer,2005.

[3]Melo M T,Mallik S,Saldanha-da-Gama F.Dynamic multi-commodity capacitated facility location:A mathematical modeling framework for strategic supply chain planning[J].Computers & Operations Research,2006，33:181-208.

[4]Klose A,Drexl A.Facility location models for distribution system design[J].European Journal of Operations Research,2005，162(1):4-29.

[5]张春民，杨 涛.公路货运枢纽选址方法的研究[J].交通科技，2006(6)：100-103.

[6]郑称德，黄 达.客户需求驱动的多层物流网络选址规划模型与算法[J].系统管理学报，2009，18(2)：232-236.

[7]孙 焰.建模理论及算法设计[M].上海：同济大学出版社，2004.

[8]胡运权.运筹学基础及应用[M].北京：高等教育出版社，2008.

[9]Hanselman D,Littlefield B.精通Matlab 7[M].北京：清华大学出版社，2006.

[10]范德林，龚 静，于慧伶.基于TRIZ理论汽车供应链核心企业的供应物流优化研究[J].森林工程，2012，28(6)：107-109.

[11]郭志军.分支定界算法的Matlab实现[J].江西教育学院学报，2007(20)：4-7.