基于蚁群算法和动态路阻的物流配送路径优化

丁柏群，姜 瑾

(东北林业大学 交通学院，哈尔滨 150040)

现阶段，我国多数物流企业对配送车辆进行调度时主要依据经验，容易导致车辆使用效率低下，基于蚁群算法研究城市配送车辆路径优化问题有很强的实用性，结合动态路阻函数的优化后蚁群算法将考虑实际路网动态交通条件的影响，其优化目标就是在满足货运车辆完成对客户要求产品需求的前提，使得所有车辆的行驶路线最合理。

1 蚁群算法基本原理

意大利学者M.Dorigo在自然界真实蚁群觅食行为的启发下于1991年首次系统地提出蚁群算法。在从食物源到蚁穴并返回的过程中，蚂蚁能在其走过的路径上分泌一种化学物质，称为信息素，并通过这种方式形成信息素轨迹[1]。蚂蚁在运动过程中能够感知信息素的存在及强度，并依此指导自己的运动方向，使蚂蚁倾向于朝着该物质强度高的方向移动，形成回到蚁穴的最短路径。

蚁群在完成觅食并返回蚁穴的过程中具有如下特征。

(1)在从节点i到节点j的运动过程中或是在完成一次循环后，蚂蚁在边(i，j)上释放一种物质，称为信息素轨迹。

(2)蚂蚁概率地选择下一个将要访问的节点，这个概率是两节点间距离和连接两节点的路径上存有信息素量的函数。

(3)为了满足问题的约束条件，在完成一次循环之前，不允许蚂蚁访问已经访问过的节点。

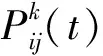
(1)

其中，allowedk={0，1，…，n-1}表示蚂蚁k下一步允许选择的节点；tabu为用于记录蚂蚁在一次循环中已经走过节点的禁忌表[3-4]。

α、β为参数，分别反映蚂蚁在运动过程中所积累的信息和启发信息在蚂蚁选择上的重要程度。

τij(t)为t时刻从节点i到节点j的信息素轨迹强度。

ηij(t)为t时刻的能见度，反映蚂蚁从节点i到节点j的可期望性。

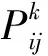
2 结合动态路阻的蚁群算法优化

在目前的配送路径规划研究中，对道路阻抗的研究很少，路阻函数是指路段行驶时间与路段交通负荷之间的关系，交通阻抗的大小将直接影响车辆对路径的选择，是动态交通分配的关键。

2.1 路阻函数建模

道路阻抗分为静态道路阻抗和动态道路阻抗，在以往的静态交通分配中，交通阻抗直接用路段长度除以实际行车速度的办法来确定，该方法仅考虑了道路条件对路阻的影响，不能体现动态交通条件对配送车辆选择路径的影响。本文考虑将静态路阻函数与动态路阻函数结合，并改进到蚁群算法中，以便于更好的得到最优路径。

(2)

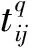
(3)

(4)

公式(4)中，当某一路段上的交通量逐渐增大，达到qij=cij后，道路上的车辆将开始产生拥挤，此时的交通密度为极限密度，若车辆仍不断增加，将导致交通阻塞，从而使车辆行驶速度为零，通过该路段的时间为无限长，则路阻函数为最大；反之，当路段上的交通量趋于零时，车辆行驶速度为自由流速度，则路阻函数为最小。

综合路阻函数Zij由层次分析法得到的静态路阻函数和实时交通流量转化的动态路阻函数相应结合得到：

(5)

式中：γ为静态路阻函数在综合路阻函数中所占的比例系数。

2.2 考虑动态路阻的蚁群算法

为考虑动态交通条件对状态转移的影响，将道路阻抗函数Zij结合进蚁群算法状态转移概率公式中：

(6)

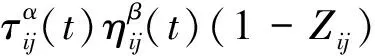
3 物流配送车辆路径优化模型

车辆路径问题可以描述为：某一配送中心负责向多个客户点运输货物，每个客户点的货物需求量为gi(i=1，2，…，n)，配送中心将派出多辆相同规格货车负责送货，求满足货物需求的最低成本的车辆运输行程路线。大部分物流企业的配货，特别是有时间窗口的配货对总行程时间的长短有所限制，对物流配送的快捷性要求较高，这里的运输成本则主要考虑时间成本，应使得所行驶线路最短为研究主要目标，但是由于实际交通条件的限制，行驶距离最短的路径不一定就是用户考虑最优的路径。

因此将各路段的距离dij经过处理转化为以行驶时间为标准，则路段上行驶时间为

(7)

在定义模型前，需要做出以下假设：

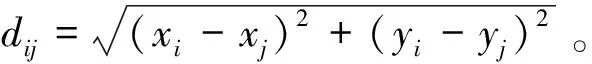
(2)配送中心的配送车辆为统一型号车辆，汽车载重量要大于在线路上经过客户点的需求量之和。

(3)每个客户点的货物需求只能由一辆车来完成。

车辆配送期望达到的目标是[3]：

(1)按照客户点的需求准时送货以提高服务质量。

(2)在保证客户需求量不超过车辆载重，同时满足车辆行经各个客户点的总行驶时间最短的前提下，使得物流配送总成本最低。

相关变量：

M为车辆总数，N为客户点数。

gi为客户的货物需求量，其中=1，2，…，n。

dij为客户i到客户j的距离，i，j=0，1，2，…，n，其中d0j表示配送中心到客户j的距离，di0表示客户i到配送中心的距离。

Q为车辆的最大装载量，假设：

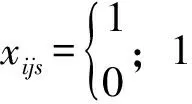
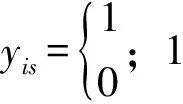
根据约束条件，建立以配送总时间最短为目标的优化目标函数为：

(8)

4 实例验证

将优化后的蚁群算法对哈尔滨某一物流配送中心向各个客户需求点配送货物实例应用验证，要求满足各分店的货物需求，安排合理的配送路线，使得实时交通路况下配送线路最优[4-7]。

在此配送案例中，依据所调查的实际情况做出以下约束：

(1)假设配送中心到各客户需求点的道路路况信息为已知，实时路况信息可以随时获得。

(2)配送中心到各客户点的距离及各客户点的货物需求量为已知。

(3)车辆在完成配送任务后要返回配送中心，各个客户必须配送到达且只能配送一次。

用0代表配送中心，1～9代表货物需求点，配送中心有载重量为5 t的相同规格配送车辆3辆，每次配送最大行驶距离为60 km。9个客户的货物需求量见表1。

表1 客户货物需求量

构建数学模型并设定相关参数：

(1)相关变量

客户数：N=9；

配送中心派出的车辆总数：M=3；

车辆的最大载重量：Q=5 t；

车辆的最大行驶距离：D=60 km。

(2)确定优化目标函数

(9)

为验证考虑路阻函数的改进蚁群算法在解决物流配送路径优化问题上的应用，使用软件对哈尔滨市某一物流配送中心所选择的9个客户点的货物配送路径优化进行配送求解。考虑蚁群算法的搜索循环次数和解的最优性，选定所需参数蚂蚁数量m=15，启发式因子α=3，启发式因子β=3，信息素的挥发系数ρ=0.5，蚂蚁释放的信息素量Q=100。

静态蚁群算法和优化后的蚁群算法由于客户点需求量的限制，对客户节点运行的结果得到的较优路径中各车辆的配送路线为：配送中心-建国街-保障街-滨江站-通达街-配送中心；配送中心-神州物流-禧龙大市场-内陆港-配送中心；配送中心-哈平西路-新疆东路-配送中心。图1和图2分别是两者得到的优化行驶路径。

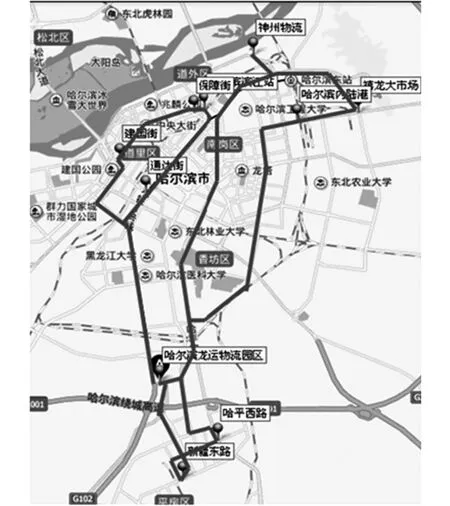
图1 静态蚁群算法的实际最优路径

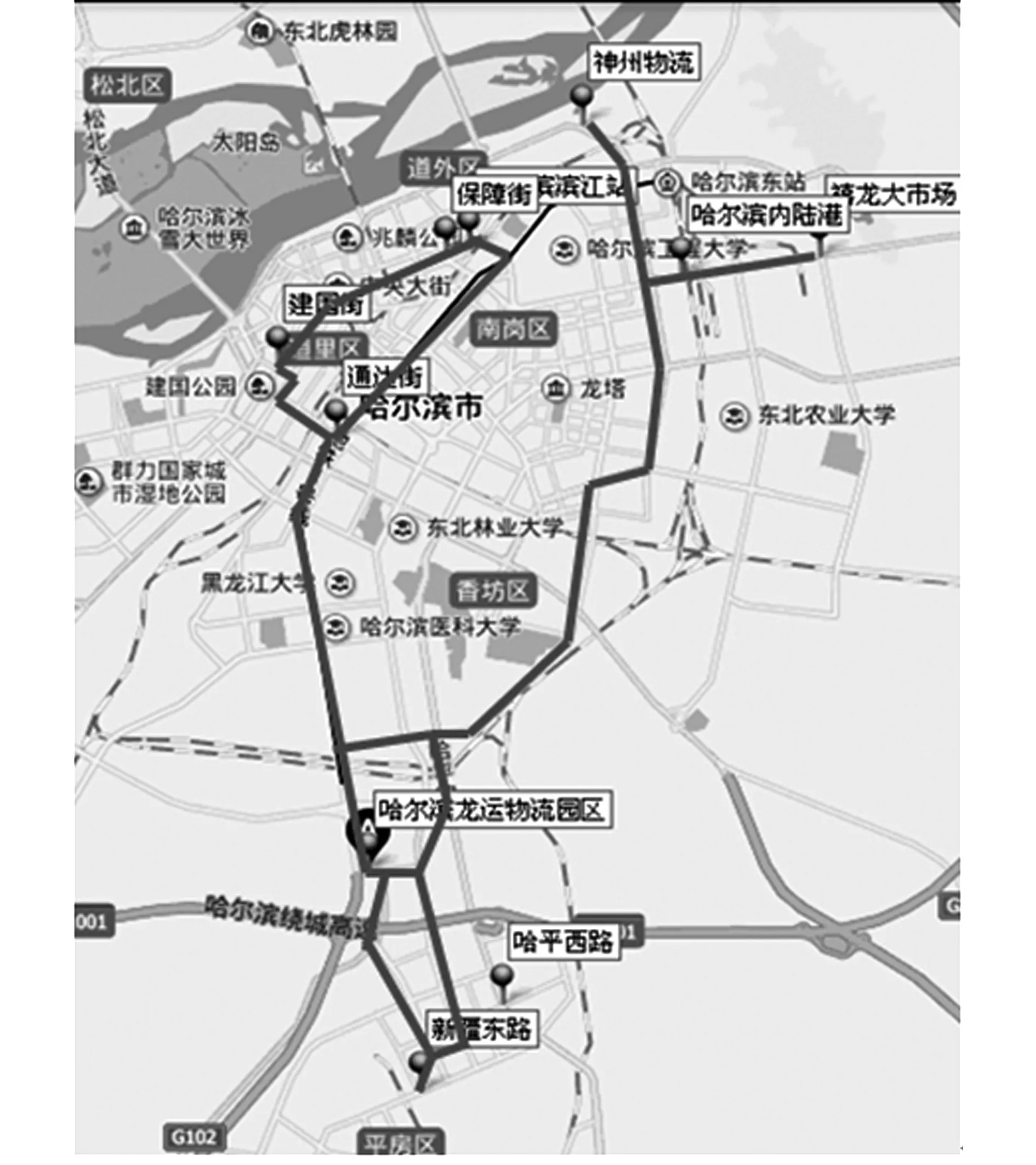
图2 动态蚁群算法的实际最优路径

根据优化目标函数，使得货物从配送中心出发到达各个客户点后返回物流中心的总行程时间最短，静态蚁群算法和优化后的动态蚁群算法的计算数据见表2。

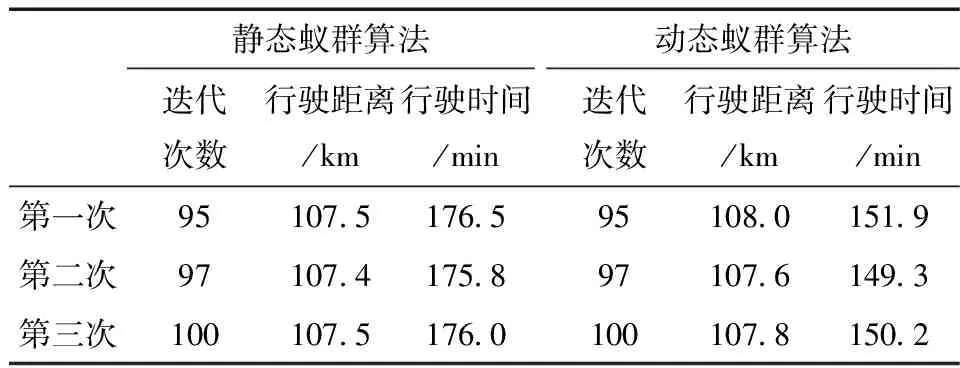
表2 两种算法的计算结果比较

从表2可以看出，融合路阻函数的蚁群算法较传统静态蚁群算法在相同迭代次数下总行驶距离相差不大，行驶时间节省了约15%左右，满足了优化目标函数使得行驶时间最短的要求，因此在求解车辆路径问题时，基于动态路阻函数的优化蚁群算法是有效的。

5 结束语

在基本蚁群算法原理和物流配送模型的基础上，考虑实际交通情况下的动态路阻函数，将其优化进蚁群算法形成动态路径优化方法，在物流中心对配送路径选择时有效缩短配送时间，在本文案例验证计算中，结合动态路阻函数的蚁群算法较静态蚁群算法节省了配送时间15%左右；通过软件开发能够将优化动态路径选择作为具有实用价值的物流管理服务系统的组成部分，为用户提供更有效路径选择的指示和导航。

【参 考 文 献】

[1] 李世勇.蚁群算法及其应用[M].哈尔滨：哈尔滨工业大学大学出版社，2004.

[2] 马 良，朱 刚，宁爱兵.蚁群优化算法[M].北京：科技出版社，2008.

[3] 尹训波.基于蚁群算法的物流配送路径优化[J].科技信息，2006，23(6).195-196.

[4] 李 慧.基于蚁群算法的物流配送路径优化[D].太原：山西大学，2011.

[5] 温惠英，沈毅贤.适于物流配送车辆导航路径规划的路网阻抗确定方法研究[J].交通科技2008，34(1).94-97.

[6] 李慧子，王尔媚，周 沫，等.甩挂运输车队运营组织模式分析[J].森林工程，2014，30(1)：157-160.

[7] 郑 远，杜豫川，孙立军.美国联邦公路局路阻函数探讨[J].交通与运输(学术版)，2007，(1).31-33.