基于RSA和密钥的二维码加密编码的研究

安吉旺，徐凯宏

(东北林业大学 机电工程学院，哈尔滨 150040)

二维码(Two dimensional Barcode)是在一维码的基础上，在垂直和水平两个方向上进行的编码和解码。QR码(Quick Response Code)作为矩阵式二维条码的典型代表，是在一个矩形空间中通过不同黑、白像素的矩阵分布进行编码。与其他二维码相比，QR码除了具有信息容量大、可靠性强，可表示汉字及图像等多种文字信息等优点外，还可全方位识读且识读速度快[1]。因此，QR码在各行各业中得到普遍应用。

一些领域，QR码所包含信息不方便被无关组织、机构和个人随意识读，这就要求其在传输和存储前进行相应的加密处理。在密码学中，信息加密有很多种方法：序列密码、分组密码、公钥密码、哈希函数等[2]，但在二维码编码技术中的应用却很少，如用Rinjdael算法分别对信息原文、密钥加密编码得到二维码A、B，A、B非功能区异或编码得到二维码C[3]；QR码二值图像DES加密将原有规律排列的黑白相间区域变成杂乱无章的黑白区域，破坏了QR码平面结构使无法识读信息[4]；结合编码规则，先用PBE(Password Based Encryption)方法对数据信息加密再把密文编码[5]。

本文结合RSA加密算法和编码规则，通过改进加密过程在VC上实现对信息的双重加密。

1 QR编码规则

QR码是由编码区域和功能图形组成一个正方形阵列。QR版本7符号结构图如图1所示。

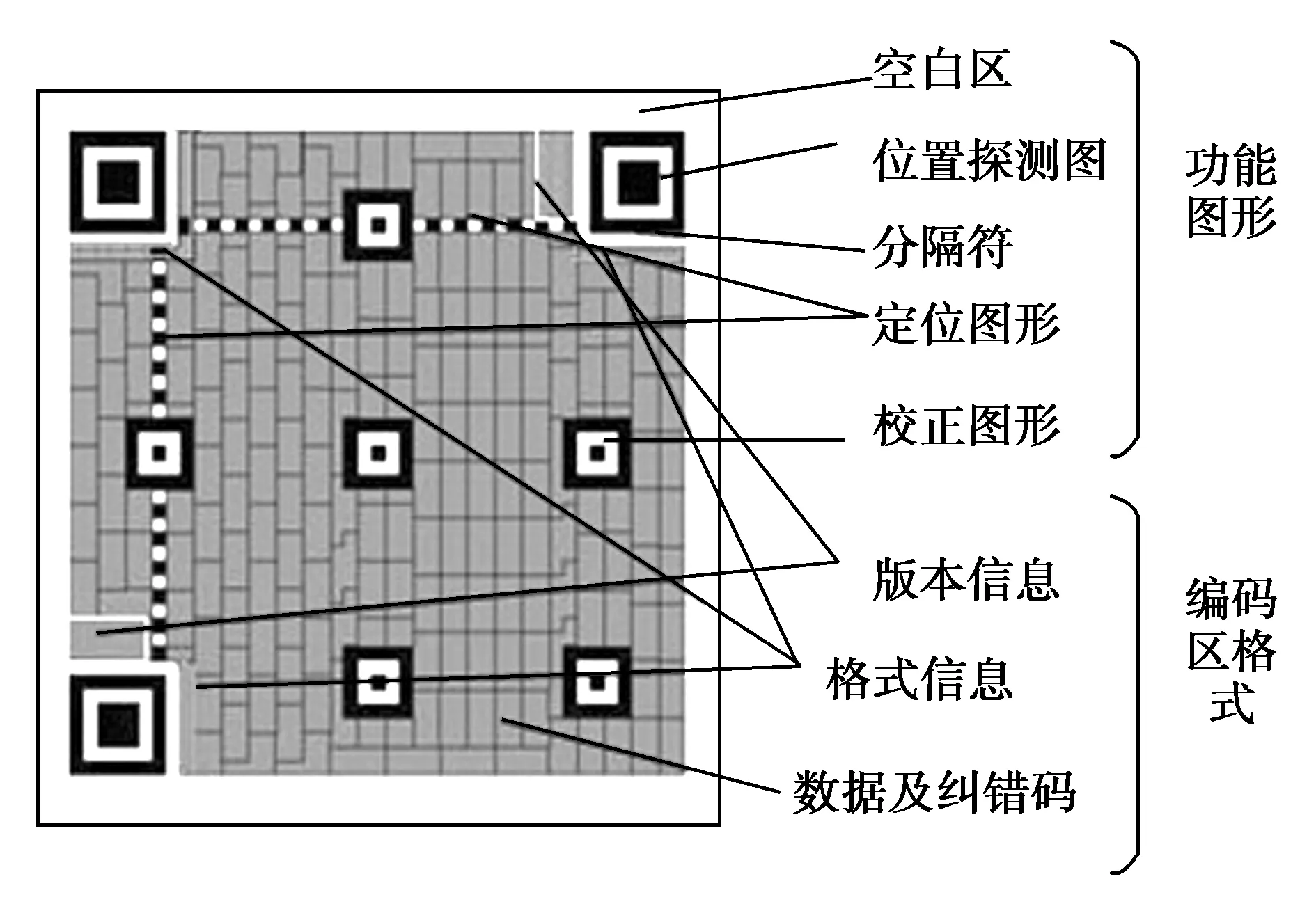
图1 QR码符号的结构

QR编码共分七个步骤：①数据分析：分析所输入的数据流，确定要进行编码的字符的类型。②数据编码：针对不同数据模式将数据转化成二进制位流，经码字转化最终形成码字位流。③纠错编码：根据选定的符号标识和纠错等级，将一组给定的数据码字分成数据块并计算相应数据块的纠错码字。④构造最终信息：依次将每一块的数据码字和纠错码字装配成最终序列码字。最终编码信息排放如图2所示。⑤在矩阵中布置模块：将上图功能图区的各个模块一起加入矩阵。⑥掩模：将数据及纠错码区域内满足条件的模块定义为深色。⑦格式和版本信息：根据编码格式和版本型号生成QR码符号[1]。

图2 编码信息排放

QR编码算法公开且编、译码软件应用普遍，未加密的QR码很容易被识别。将加密引入到二维码技术中，对于食品安全、票务管理、贵重物品防伪等方面都有很大的帮助，这也促进了二维码技术的普及。

2 RSA算法

RSA密码体制是由Rivest，Shamir，Adleman于1978年提出的基于数论理论的公钥密码体制，是目前应用最广泛的公钥密码体制。加密体制如下：

密钥生成：用户任意选取两个大素数(大于500比特)p、q，计算公式：

n=pqφ(n)=(p-1)(q-1)。

(1)

随机选取一个整数e：1≤e<φ(n)且e与φ(n)互质。通常先选定e，再找出并确定p，q。求解私钥d：1

for(i=0；i

{

j=i*e%k；

if(j==1)

{

printf(“%d”i)；

printf(“ ”)；

}

}

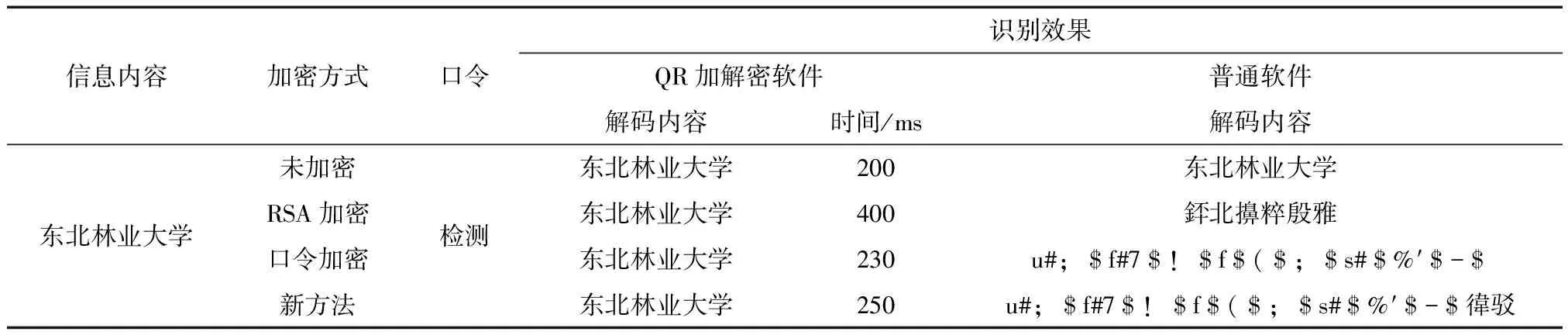
其中，n为运算模数，e为加密指数，d为解密指数。在编码过程中为可公示密钥。为非公开的私钥，信息接收端若要获取加密信息必须申请私钥。

加密算法：首先将明文分组，每组长度小于log2n。使用公钥对每个分组m加密生成密文c：c=memodn。

解密算法：在知道私钥k的情况下解密密文c得到明文m：m=cdmodn。

3 密令Key算法

此算法是采用输入密钥k加密明文m使其转化成可视字符的算法。算法规则如下：

加密算法：获取明文m、密钥k，明文和密钥是以字符型输入。将明文m按密钥k的字符长度分段成，m1，m2，…，mn，若不能整除则加入填充符“ ”。分别自密钥k和每段数据符mi的首字节开始提取字节数值k1、k2。通过Ci=((k1+k2+512)mod 95)+32(实验证明汉字字符字节提取值为负值)运算将明文字符mi转化成ASCⅡ码表中32～126之间的可视字符c1,c2,…cn。加密过程中(k1+k2+512)/95的值加32同样转化成ASCⅡ码表中32-126之间的可视字符q1,q2,…qn，最后得到密文

c=c1,q1,c2,q2,…cn,qn。

解密算法：解密是加密的逆过程，获取密文c、输入正确的密钥k，明文和密钥是以字符型输入。先提取密文c中的q1,q2,…qn，将密文剩余信息密钥k的字符长度分段成c1,c2,…cn(此时密文c必被整除)。分别自密钥k和每段数据符ci的首字节开始提取字节数值k1、k2。通过mi=k2+95*Q[n]-512-k1(Q[n]中存放加密过程中qi-32的值；i=1，2，…，n)运算最后得到明文m=mi,m2,…mn[2]。

4 双重加密编码编程实现

4.1 加密流程

图3 双重加密流程

为了不破坏QR码的符号结构、降低纠错能力及识读效率，本文将加密算法作用于QR码编解码步骤中“数据编码”步骤前，对原始数据进行加密，之后再将密文进行“数据编码”直至生成QR符号。解码则是编码的逆过程。QR码信息的双重密算法流程为：

(1)获取要加密的明文信息(汉字、图像、数字等)，并将信息进行字符转换，输入加密口令。

(2)将明文信息字符采用加密口令Key进行密文C1；

(3)对密令进行RSA算法加密生成C2；

(4)设置密码标志位，将密码C2填充到C1当中形成最终密文C。

(5)对密文C进行数据分析和数据编码，形成数据位流。

(6)对数据位流进行纠错、掩膜等后续处理直至生成加密QR码。

4.2 QR码加密实现

QR码双重加密解密的实现是采用C++语言编写，在已有开源项目和基础函数库的基础上进行的二次开发。本文在开源项目QR码的编码过程中编写函数进行加密操作。

(1)提取明文信息。明文的形式有很多种，其中，最主要的是文本信息和图像。加密所需的明文必须采用的字符串的格式，这就要求对所获取的明文进行格式转换。对于文本内容来说其本身就是字符串形式得，加密前只需获取文本信息即可。对于图像信息来说，加密编码前需要对其进行图形调整以达到相应的规格标准。

①文本信息提取：

CString strFilter= “TXT

Files(*.txt)|*.txt|All

Files(*.*)|*.*||”；

CString strCon=“(TXT file)*.txt”；

…

m_strTxtFileName=fDlg.GetPathName()；

②图像信息提取：

strFilter=“Bitmap Files(*.bmp)|*.bmp|All Files(*.*)|*.*||”；

strCon=“(Bitmap file)*.bmp”；

…

m_strBmpFileName=fDlg.GetPathName()；

…

sprintf(ss，“%s”，m_strBmpFileName.GetBuffer(256))；

SizeDIB(ImgFileName，100，100)；//调整图像

(2)双重加密。

①口令key加密：将上面提取的文本信息TxtFile-

Name、图像信息ImgFileName，作为加密明文Source，在输入口令Key的前提下进行加密。

CString CEncryptDlg∷Encrypt_Key(CString Source，CString Key)

{

…

k1=pKey[j-1]；

k2=pSource[j-1]；

intk=k1+k2+512；

div_Result=div(k，ENCRYPT_KEY)；

k=div_Result.rem；

m=div_Result.quot；

pMid[j-1]=k；

strTarget[n]=k；

DstrTarget[n]=m；

n++；

…

i=0；x=0；

for(j=0；j<2*n；j++)

{

if(j%2==0)

sstrTarget[j]=strTarget[i++]+32；

else

sstrTarget[j]=DstrTarget[x++]+32；

}

…

}

②RSA加密：对口令Key加密，将Key作为RSA加密算法的输入m_Source

wsprintf(pSource，“%s”，m_Source)；

iLen=m_Source.GetLength()；

for(i=0；i

{

div_t div_Result；

dw1=Exp(pSource[i]，e，r)；

div_Result=div(dw1，r)；

pTarget[i]=div_Result.rem；

//获取密文

}//加密算法最关键是引用Exp()函数，是RAS加密的核心算法。

DWORD Exp(intk，inte，intr)

{DWORD dwResult；

div_tdiv_Result；

dwResult=k；

div_Result=div(dwResult，r)；

dwResult=div_Result.rem；

for(inti=1；i

{dwResult*=k；

div_Result=div(dwResult，r)；dwResult=div_Result.rem；}

return(dwResult)；

(3)编码函数

QR编码只需在获取加密密文后调用Qr_code编码动态链接库EnCodeQr.dll

void BarCodeDlg：：EnCoding()

{…

SetQrConFile(m_strConFileName)；//设置QR配置文件

if(imgLen<1)

…

barname=EnQrText(m_strInfo)；//将信息生成QR码不含编码信息结构

else

…

barname=MakeQrCode(TxtFileName，ImgFileName，“”)；//将文本、图形和其他信息合成生成QR码，含编码结构信息。}

5 实验及分析

本文采用汉字模式下“东北林业大学”为加密原文，编码QR图像如图4所示，其中图4(a)未加密，能够采用普通识别软件读取，而图4(b)、(c)、图4(d)分别采用RSA、密令Key、RSA改进算法加密QR码，必须采用专用识别软件才能正确识读。

图4 不同加密方式下生成的二维码

从QR码加解密测试数据(见表1)可以看出，加解密软件可正确识读加密和未加密QR码，而普通的识读软件对加密QR码的正确识别率为0%。本实验中若对“东北林业大学”进行单一RSA算法加密且公钥e=101，其中求余运算1 224次、加法运算1 212次。采用本文的改进算法加密：求余运算417次、加法运算457次。通过对运算次数和加、解密时间的分析，新加密方法效率更高，安全性更强。另外新的加密方法：加密口令简单、灵活，且由用户掌握。对比加密前后的QR码符，其结构并未改变，不影响QR码的适度效率。

表1 QR码加解密测试数据

6 结束语

RSA算法是基于分解大整数的困难性的加密，在管理密钥方面算法优越，加密时公钥更新容易，对外只需保密私钥。但RSA算法计算复杂，其模正整数次幂运算需消耗大量时间，当进行大信息量加密时将严重影响加解密的执行效率。本文研究了QR码编解码规则和RSA改进加密算法，针对QR码信息加密的缺陷，提出采用输入口令加密原文信息、RSA算法加密口令的算法。通过实验证明，本方法在未知私钥的情况下采用普通识别软件对QR码的正确识别率为0%，既保证了信息的安全性又提高了加密的灵活性和提高了效率，具有很强的实用性，可得到广泛应用。

【参 考 文 献】

[1] 中国物品编码中心，二维码技术与应用[M].北京：中国计量出版社，2007.

[2] 郑 东，李祥学，黄 征.密码学——密码算法与协议[M].北京：电子工业出版社，2009.

[3] 任勇金.基于Rijndeal和异或运算的QR二维码双重加密研究[J].华章，2012(29)：338.

[4] 刘彦伟，王根英，刘 云.QR码信息加密的研究与实现[J].推广与应用，2012，21(11)：37-41.

[5] 李 东.基于加密和解密的二维条形码的实现[J].科学传播，2010，(7)：114-115.