MP算法在地震波阻抗反演中的应用

周东勇, 文晓涛, 贺振华, 蒲 勇, 黄德济, 胡军辉

(1.油气藏地质及开发工程国家重点实验室(成都理工大学),成都 610059;2.中国石化股份有限公司 勘探南方分公司,成都 610041)

波阻抗反演开始出现于20世纪70年代初，是一种以研究岩性油气藏为主的地震勘探技术。目前，波阻抗反演的方法有很多，如模拟退火法、遗传算法等等。本文研究采用匹配追踪算法对地震数据进行分解，得相对反射系数，进而依据波阻抗公式进行波阻抗反演。匹配追踪算法(Matching Pursuits，本文统一简写为MP算法)由Mallat和 Zhang于1993年首先提出[1]，之后很快被应用于地震信号处理领域。2003年Castagna等将MP算法用于地震谱分解[2]; 2007年Y.H.Wang将该算法应用于时频分析[3]；2012年张繁昌等将该算法用于瞬时谱识别来确定三角洲砂体尖灭线[4]等等。虽然应用MP算法对信号稀疏分解时，计算量十分大，但该算法有很多优良的性质,如对信号自适应的灵活表达，较高的时间、频率分辨率,暂态结构的局部自适应性,信号结构的参数表示更加灵活等[5]。

1 地震信号的稀疏分解

信号表示实际上就是把给定的信号在已知的函数集(函数集中的任意一个函数称为基函数)上进行分解, 然后在变换域上表达原始信号或原始信号的主要成分。若在变换域上用尽量少的基函数来表示原始信号或原始信号的主要成分, 就是信号的稀疏表示, 得到信号稀疏表示的过程就是信号的稀疏分解[6]。若用这种分解过程分解地震信号，则是地震信号的稀疏分解。MP算法就是实现地震信号稀疏分解的算法之一。

设研究的地震信号为f,信号长度为N,且f∈H，H为希尔伯特空间。MP算法将原始地震信号f稀疏表示为

(1)

式中:gγi为函数集中的基函数(在MP算法中函数集被称为过完备原子库，基函数被称为原子);ci为地震信号f在基函数gγi上的投影分量[7]。式(1)和条件n≪N集中体现了地震信号稀疏表示的思想。地震信号在过完备原子库上的分解结果一定是稀疏的[1]。

2 过完备原子库的建立

如何建立合理的过完备原子库对能否精确匹配地震信号至关重要[8]。雷克子波与地震子波的波形相似，适合分析地震信号的特性，在地震反演中得到了广泛的应用。此处，笔者提出利用非零相位雷克子波来构建过完备原子库的思想，实现对地震信号的稀疏分解。

2.1 零相位雷克子波

Ricker子波表达式如下[9]

r(t-μ)=[1-2(πfp(t-μ))2]e-(πfp(t-μ))2

(2)

式中:fp为峰值频率[10]；μ为时间延迟；e为自然对数。其波形是由1个主瓣2个旁瓣组成，图1为30 Hz、50 Hz雷克子波波形图。

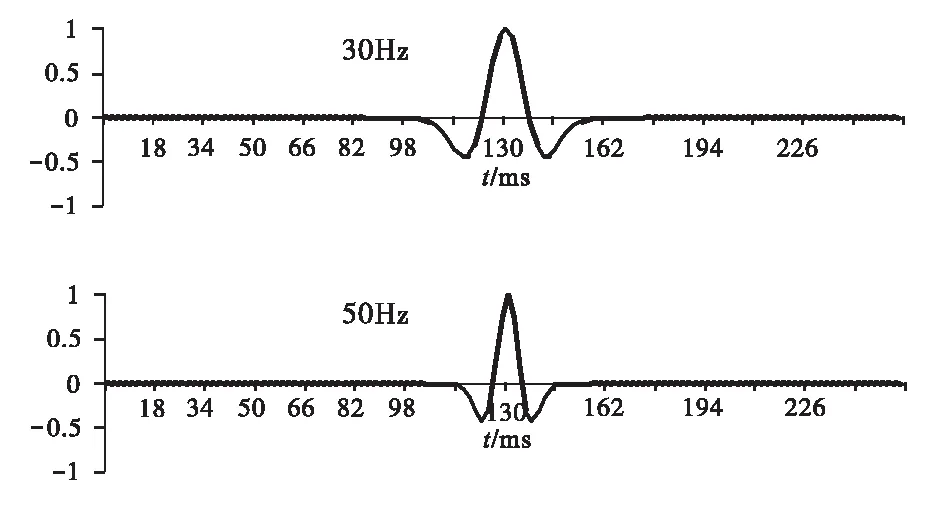
图1 30 Hz、50 Hz雷克子波波形图Fig.1 The shape of Ricker wavelets for 30 Hz and 50 Hz

2.2 非零相位雷克子波

本文采用的非零相位雷克子波，由解析信号推导而来[11]。以下是Ricker子波经ω相位旋转后的表达式

r′(t)=r(t)cosω-r*(t)sinω

(3)

其中:r(t)=[1-2(πfpt)2]e-(πfpt)2;r*(t)为r(t)的Hilbert变换。

对Ricker子波分别进行30°、90°、150°和180°相位旋转后如图2所示。

2.3 过完备原子库

过完备原子库D={gγ}γ∈Γ由非零相位雷克子波公式经离散化、归一化形成，为叙述方便现将非零相位雷克子波公式写成

gγ∈Γ(t-u)=r(t-u)cosω-r*(t-u)sinω

(4)

式中:r(t)为雷克子波；r*(t)为雷克子波的希尔伯特变换；γ=(fp,ω,u)是时频参数；Γ是所有时频参数的集合。fp为主频参数；ω为相位参数；u为位移参数。时频参数可以按下式离散化

γ=(i·dfp,j·dω,n·du)

(5)

然后通过式‖gγ(t)‖=1将每个原子归一化。

在过完备原子库中，1个原子gγ(t)由参数(fp,ω,u)决定。参数(fp,ω)决定原子gγ(t)的波形，而参数u只决定原子gγ(t)出现的位置。

3 基于MP算法的波阻抗反演流程

3.1 MP算法原理

设f为待分解的地震信号，D为用于分解地震信号的过完备原子库，gγ为过完备原子库D中的原子，gγ∈D, ‖gγ‖=1。

MP算法分解地震信号f过程如下。

(1)从过完备原子库D中选择与地震信号f最为匹配的原子(即为最佳原子)gγ0，使其满足以下条件

|〈f,gγ0〉|=sup|〈f,gγ〉|

(6)

其中，〈f,gγ〉错误！未找到引用源。f与原子库中任意原子gγ的内积，sup在泛函分析中称为上确界，此处即为最大值的意思。

此时可将地震信号f分解为

f=〈f,gγ0〉gγ0+R1f

(7)

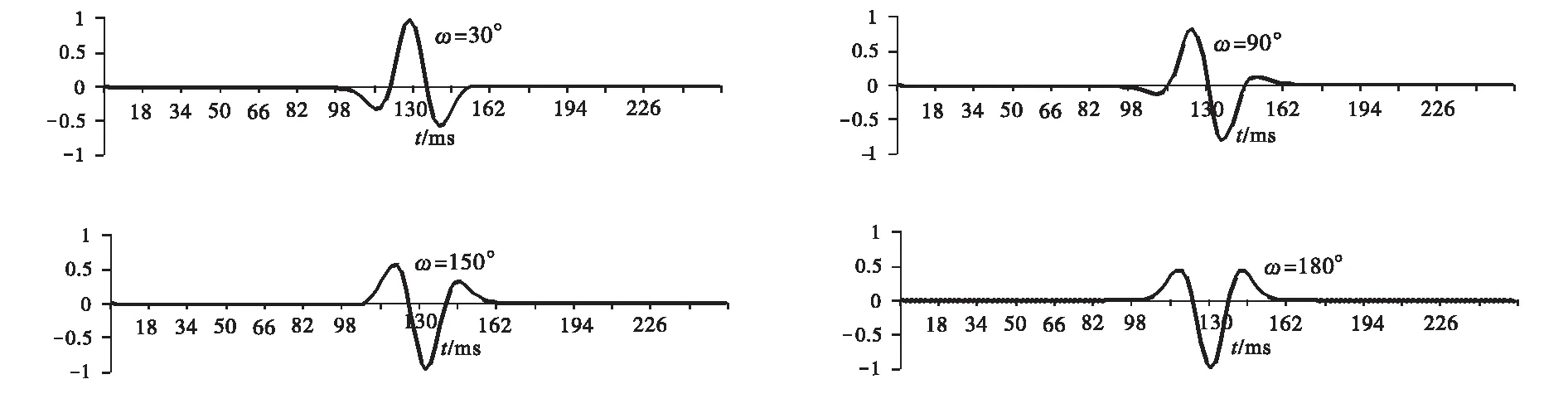
图2 30°、90°、150°和180°相位雷克子波波形图Fig.2 The shape of Ricker wavelets for 30°, 90°, 150° and 180°

其中R1f为地震信号f与最佳原子gγ0匹配后的剩余地震信号(即为残差)。

由于gγ0与R1f正交，所以其能量表示为

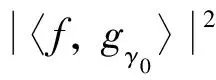
(8)

(2)将剩余地震信号(或残差)看做新地震信号，重复以上过程，不断将新地震信号匹配到过完备原子库上，经过k+1次匹配可以得到

Rkf=〈Rkf,gγk〉gγk+Rk+1f

(9)

其中gγk满足

|〈Rkf,gγk〉|=sup|〈Rkf,gγ〉|

(10)

由于Rk+1f与grk正交，则有

(11)

(3)经过n次分解后最终把地震信号f分解为

(12)

能量分解为

(13)

此处，令f=R0f,Rnf为原地震信号分解为n个最佳匹配原子的线性组合后所产生的误差。

(4)分解完成的判定。MP算法是一个不断迭代的过程，需要一定的标准来判定分解是否完成。笔者认为，通过设定残差Rnf的能量阈值，来作为分解结束条件的方法是较好的判定标准。即当能量值满足‖Rnf‖2<ε(N)时，分解停止；否则继续运行直到满足条件。其中ε(N)为与采样点N相关的阈值，可根据经验自行设定。

3.2 波阻抗反演流程

为更好地描述波阻抗反演过程，设计如图3所示流程图。整个流程大体可分为两部分：首先通过MP算法不断匹配地震信号或剩余地震信号，获取相对反射系数及其对应位置；第二依据波阻抗递推公式(14)计算波阻抗。

(14)

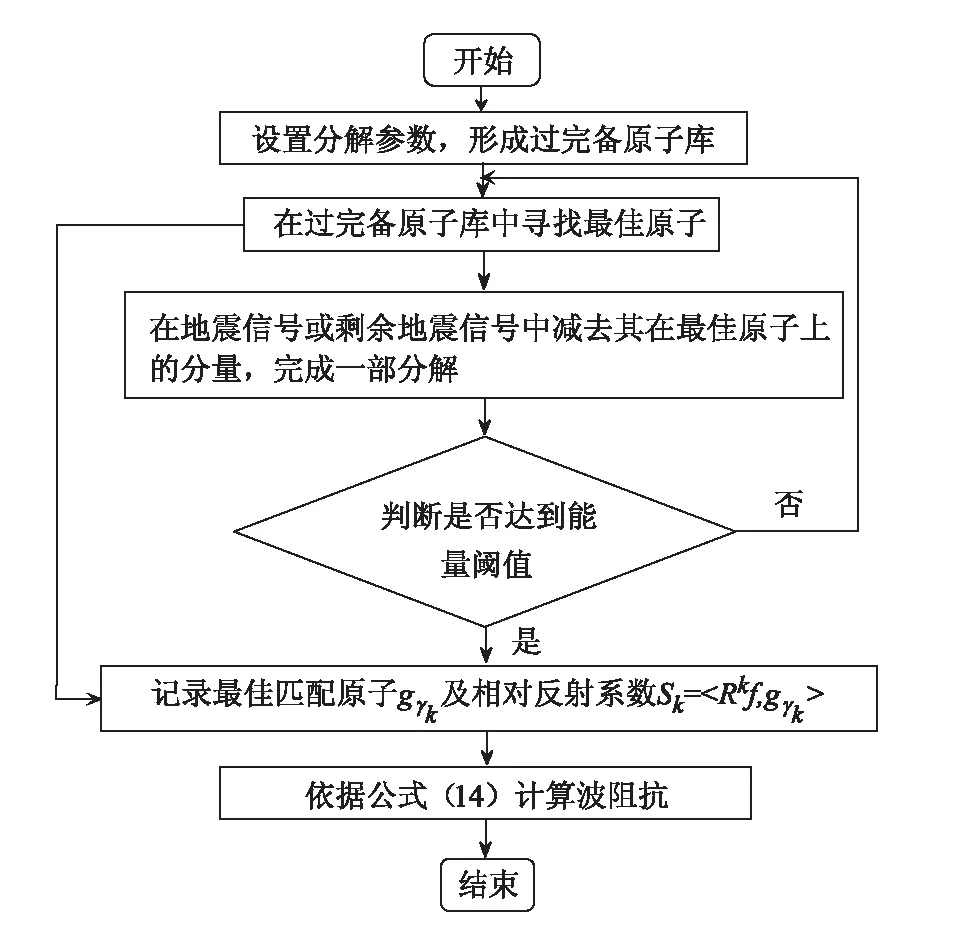
图3 基于MP算法地震波阻抗反演流程流程图Fig.3 The workflow of seismic wave impedance inversion based on MP algorithm

图中，因实际地震数据中的反射系数一般在±0.3之间，故将相对反射系数sk约束到±0.3之间，得近似反射系数Sk；初始波阻抗Z0由模型给出。

4 基于雷克子波原子库的MP算法用于地震波阻抗反演的可行性

为了验证算法的有效性，笔者用合成单道地震信号和楔形地震正演模型2种方法分别进行了MP算法反演测试。其中，前者主要是验证MP算法用于地震信号分解的可行性，测试其对地震信号分解的精度；后者主要是简单模拟实际地震数据，验证其对地震波阻抗反演的宏观效果。

4.1 MP算法用于地震信号稀疏分解的可行性及其分解精度分析

为验证其对地震信号稀疏分解的可行性及分解精度，设计了3种合成地震信号。3种合成地震信号除第二层反射系数的位置不同外，其他均采用相同参数的雷克子波(此处雷克子波长度λ为40个采样点，2 ms采样，其参数如表1所示)合成长度为N(此处N为128个采样点，2 ms采样)的地震信号。合成地震信号第二层反射系数的位置分别取在第90、60、50个采样点上，分别依次为两层间无调谐、λ/2调谐、λ/4调谐3种情况。

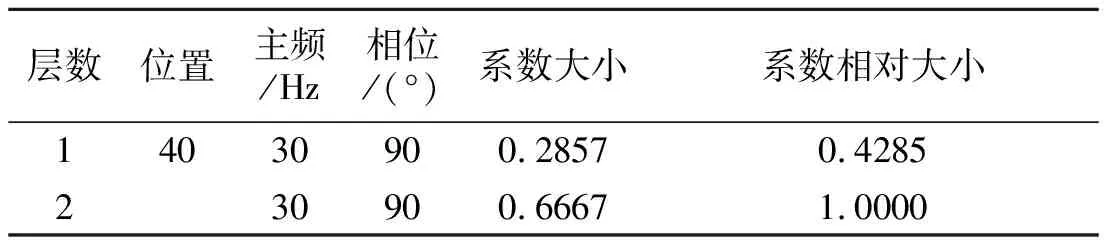
表1 合成地震信号所需雷克子波参数Table 1 The Ricker wavelet parameter for the synthetic seismic signal

4.1.1 两层间无调谐(两层间厚度大于λ)时

对比图(图4-C和图4-A对比、图4-D和图4-B对比)和列表(表2和表1相应参数对比)可得出：两层间无调谐时，层位、主频、相位及系数的相对大小都能被准确反演出；重构地震信号和合成地震信号几乎完全相同；残差基本为零。

4.1.2 两层间λ/2调谐(层间厚度为λ/2)时

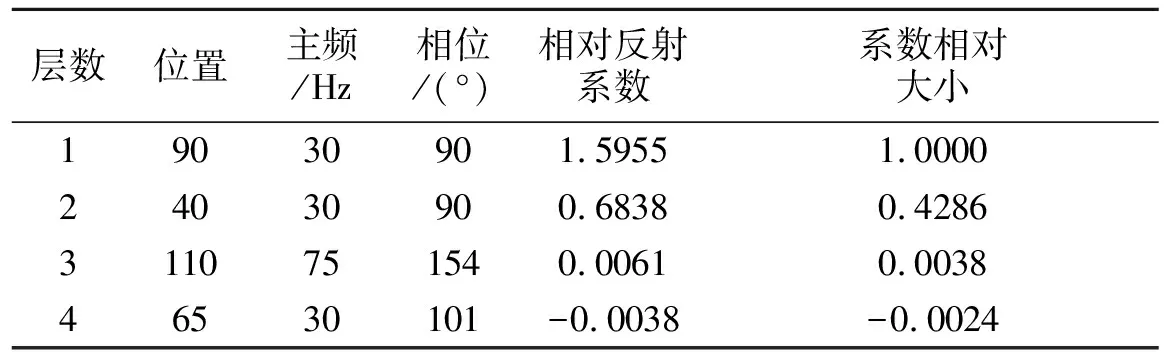
表2 MP算法分解两层间无调解的地震信号所得雷克子波参数Table 2 The Ricker wavelet parameters from the synthetic seismic signal

对比图(图5-C和图5-A对比、图5-D和图5-B对比)和列表(表3和表1相应参数对比)可得出：两层间λ/2调谐时，反演出的层位、主频及系数的相对大小与真实值相比有偏差，但偏差不大；反演出的相位与真实值相比偏差较大；重构地震信号和合成地震信号基本相同；残差趋近于零。

4.1.3 两层间λ/4调谐(层间厚度为λ/4)时

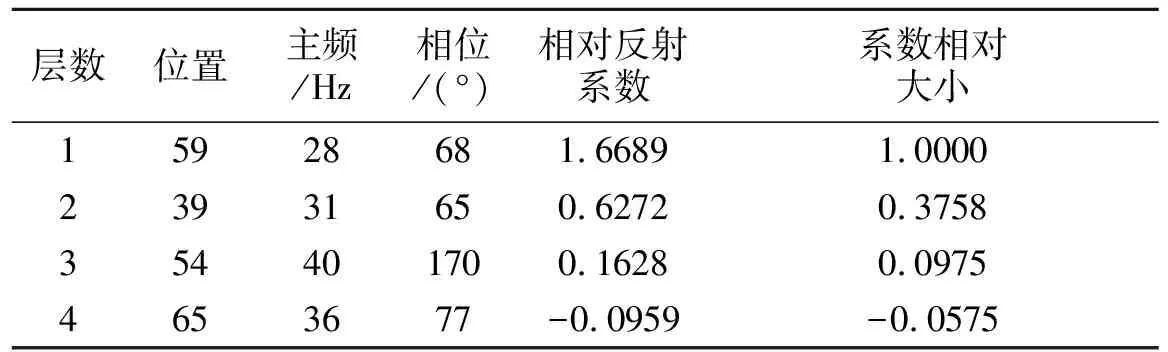
表3 MP算法分解两层间λ/2调解的地震信号所得雷克子波参数Table 3 Ricker wavelet parameters from that MP decomposes seismic signal when λ/2 tunes

图4 层间无调解时合成地震信号及反演结果Fig.4 Synthetic seismic signal & inversion results without the tuning between layers(A)反射系数; (B)合成地震信号; (C)相对反射系数; (D)重构地震信号; (E)残差

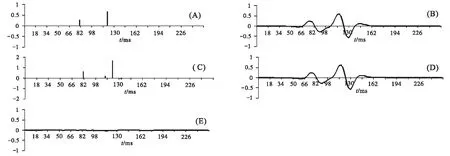
图5 层间λ/2调解时合成地震信号及反演结果Fig.5 Synthetic seismic signal and the inversion result when λ/2 tunes(A)反射系数; (B)合成地震信号; (C)相对反射系数; (D)重构地震信号; (E)残差

图6 层间λ/4调解时合成地震信号及反演结果Fig.6 Synthetic seismic signal and the inversion result when λ/4 tunes(A)反射系数; (B)合成地震信号; (C)相对反射系数; (D)重构地震信号; (E)残差

对比图(图6-C和图6-A对比、图6-D和图6-B对比)和列表(表4和表1相应参数对比)可得出：两层间λ/4调谐时，反演出的主频、相位与真实值相比偏差较大，层位和系数相对大小分别与真实值相比都有偏差，但偏差不大，仍可反映层的大体位置和系数的相对大小关系。重构地震信号和合成地震信号也基本相同，残差趋近于零。

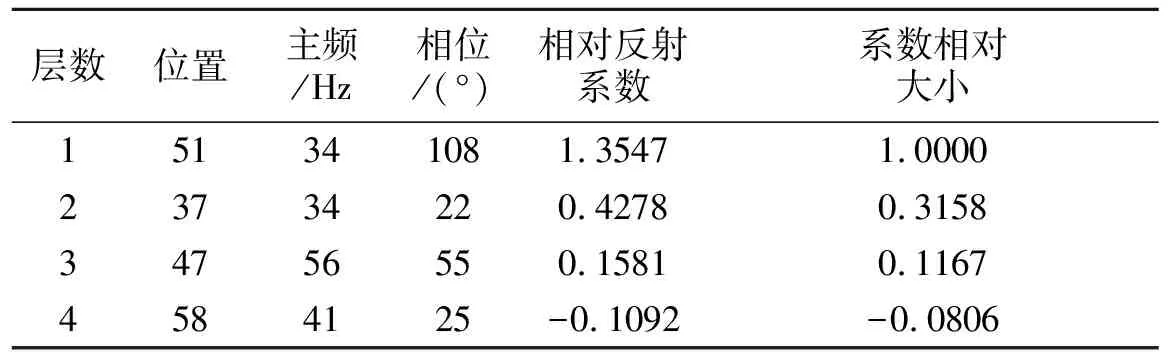
表4 MP算法分解两层间λ/4调解的地震信号所得雷克子波参数Table 4 Ricker wavelet parameters from that MP decomposes seismic signal when λ/4 tunes

通过以上对比分析可知，MP算法可用于地震信号的稀疏分解；在精度方面，两层间λ/4调谐时，仍可大体反映层位和系数的相对大小关系。

4.2 MP算法用于楔形地震正演模型波阻抗反演分析

本节主要通过反演楔形正演模型来验证该算法对实际地震数据的适用性，同时可观察其对模型的波阻抗反演宏观效果。为不失一般性，本节所用楔形正演模型(图7-C)是由任意频率、任意相位的雷克子波合成。

通过反演结果与模型对比(图7中，(E)与(B)对比、(D)与(A)对比)可以得出：两层间>λ/4时，可基本完全反演出模型中的信息；两层间≤λ/4时，与模型相比虽略有些偏差，但仍可反映楔形模型的楔形趋势。

5 实际地震数据波阻抗反演结果分析

该研究区域为塔河YY区，该区三叠系构造较平缓，主要受NE向断裂带和盐体的塑性活动控制，沿NE方向延伸形成大型圈闭群。三叠系发育的储层主要有上、中、下3个油组的砂体。本文针对中油组砂体进行研究。从图8-B中可看出，椭圆区域可能为砂体储层，与实钻情况吻合，验证了该方法的有效性。

6 结 论

本文将Mallat和 Zhang提出的MP算法应用于地震波阻抗反演中，模型试算和实际地震数据都对其有效性进行了验证，并得出以下结论。

a.MP算法能够实现对地震信号的自适应分解, 模型试算表明，其对地震信号分解的适用性，且分解精度相对较高。

b.对实际地震数据的运算与实钻情况吻合，验证了该方法的有效性，可为储层预测提供有利依据。

c.地层厚度<λ/4时，MP算法计算出的相对反射系数误差可能会偏大。因此，进一步提高该算法应用于地震信号分解的精度，更精确地反演地下地质体的波阻抗信息是笔者下一步的研究方向。

在本文成文过程中，作者与蔡涵鹏博士、高刚博士、杨小江同学及贾玉婷同学进行了有益的探讨，在此向他们表示衷心的感谢。

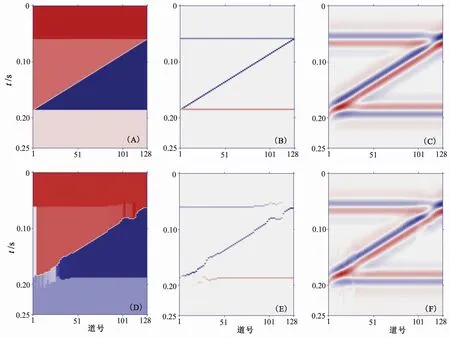
图7 地震楔形模型及MP算法反演成果图Fig.7 Seismic model and the inversion result of MP algorithm(A)波阻抗模型; (B)反射系数模型; (C)合成地震记录; (D)反演出的相对波阻抗; (E)反演出的相对反射系数; (F)重构地震信号

图8 实际地震数据及其反演成果图Fig.8 Actual seismic data and the result of inversion(A)塔河YY地区实际地震剖面图; (B)实际地震数据波阻抗反演成果图

[参考文献]

[1] Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41: 2297-3415.

[2] Castagna J P, Sun S J, Roberb W S. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127.

[3] Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit [J]. Geophysics, 2007, 72(1): 13-20.

[4] 张繁昌，李传辉，印兴耀．三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]．石油地球物理勘探，2012，47(1)：82-88．

Zhang F C, Li C H, Yin X Y. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geophysical Prospecting, 2012, 47(1): 82-88. (In Chinese)

[5] 屈念念，刘江平，李家斌．Riker子波匹配追踪算法及其改进[J]．工程地球物理学报，2009,6(6)：740-745．

Qu N N, Liu J P, Li J B. Revised matching pursuit algorithm using Ricker wavelets[J]. Chinese Journal of Engineering Geophysics, 2009, 6(6): 740-745. (In Chinese)

[6] 程文波，王华军．信号稀疏表示的研究及应用[J]．西南石油大学学报:自然科学版，2008，30(5)：148-151．

Cheng W B, Wang H J. The research and application of sparse signal representation[J]. Journal of Southwest Petroleum University (Science& Technology Edition), 2008, 30(5): 148-151. (In Chinese)

[7] 邵君，尹忠科，王建英，等．信号稀疏分解中过完备原子库的集合划分[J]．铁道学报， 2006，28(1)：68-71．

Shao J, Yin Z K, Wang J Y,etal. Set partitioning of the over-complete dictionary in signal sparse decomposition[J]. Journal of the China Rall Way Society, 2006, 28(1): 68-71. (In Chinese)

[8] 黄捍东，郭飞，汪佳蓓，等．高精度地震时频谱分解方法及应用[J]．石油地球物理勘探，2012，47(5)：774-780．

Huang H D, Guo F, Wang J B,etal. The method and application of high precision seismic spectrum decomposition[J]. Oil Geophysical Prospecting, 2012, 47(5): 774-780. (In Chinese)

[9] Ricker N. The form of laws of propagation of seismic wavelets[J]. Geophysics, 1953, 18(1): 10-40．

[10] 云美厚，丁伟．地震子波频率浅析[J]．石油物探，2005，44(6)：578-581．

Yun M H, Ding W. Analysis of seismic wavelet frequency[J]. Geophysical Prospecting for Petroleum, 2005, 44(6): 578-581. (In Chinese)

[11] 王纯伟．MP算法在地震信号去噪中的应用研究[D]．成都：西南交通大学档案馆，2010．

Wang C W. The Application Research of Matching Pursuit in Seismic Signal Denoising[D]. Chengdu: The Archive of Southwest Jiaotong University, 2010. (In Chinese)