基于系统开环频率特性曲线的奈奎斯特判据用法研究
韩俊青
(德州职业技术学院 电气系,山东 德州 253034)
0 引言
自动控制系统中解决系统稳定性问题是根据系统的开环频率特性曲线来判断闭环系统的稳定性[1],并进而确定系统的相对稳定性,奈奎斯特稳定判据解决了这一问题[2],但在实际应用过程中如何能全面深刻的理解这一判据的含义,并能灵活地运用它,还不够完善,本文基于奈奎斯特判据,通过分析系统中奈氏曲线研究这一问题.
1 奈奎斯特曲线轨迹
对于最小相位系统[3](传递函数中没有S右半平面极点和零点的环节或系统),利用幅相频率特性的起点、终点及变化趋势可准确而快速地画出曲线.对于特别复杂的系统,也可利用MATLAB[4]工具软件来描绘图形.
假设n阶系统的开环传递函数为:
(1)
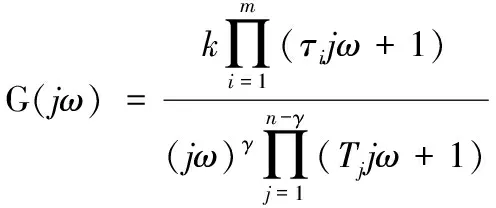
(2)

(3)
因γ值的不同G(jω)的起始段分别起始于不同的象限见图1
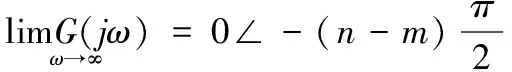
(4)
G(jω)以确定的角度收敛于坐标原点 见图2
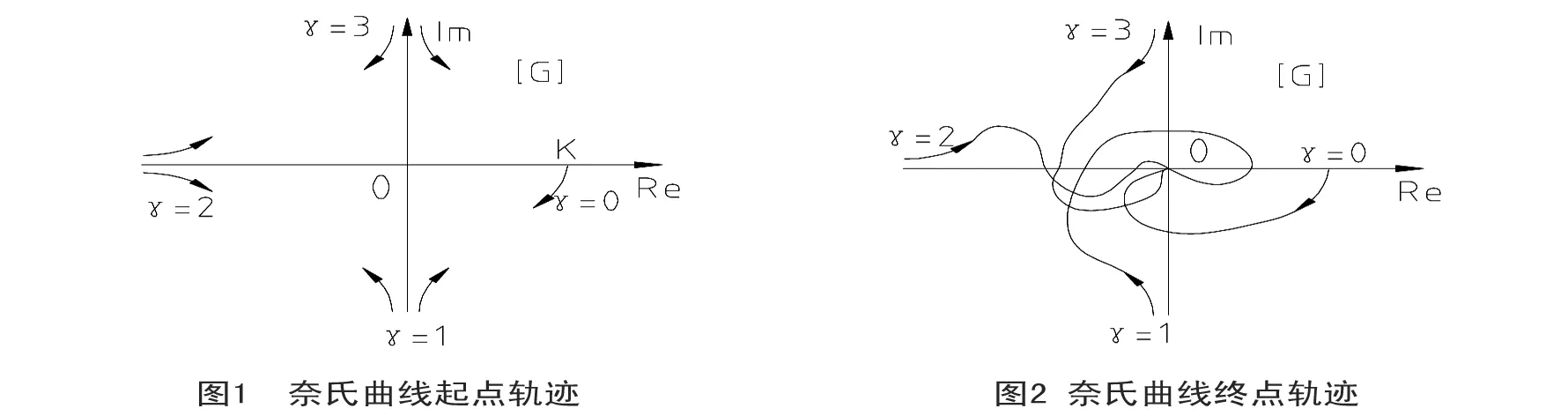
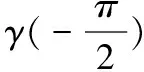
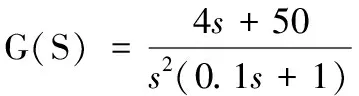
(5)

(6)
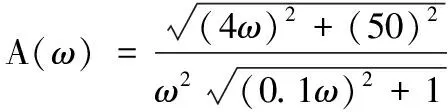
(7)
(8)

(9)

(10)
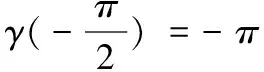
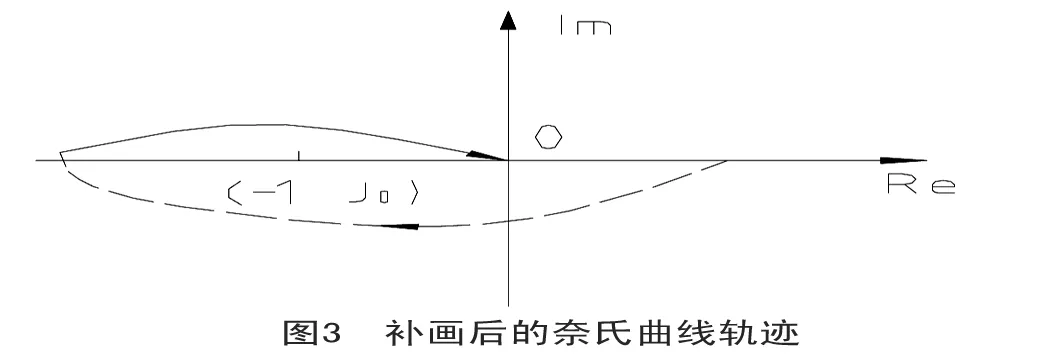
2 奈氏判据应用
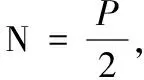
奈氏判据实际应用如下:

图4判据应用如下: 图5判据应用如下:
∵N+=0N-=0 ∵N+=0N-=1
N=N+-N-=0 p=0 N=N+-N-=-1 p=0
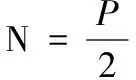
∴系统稳定 ∴ 系统不稳定
Z=P-2N=0-(-1)×2=2
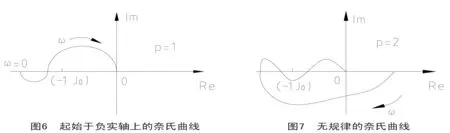
图6判据应用如下: 图7判据应用如下:

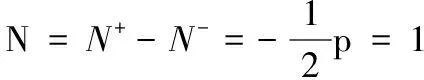
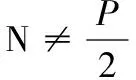
∴ 系统不稳定 ∴ 系统不稳定
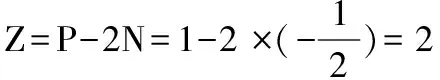
3 结束语
对于利用系统开环频率特性曲线判断闭环系统稳定性的问题,只有能正确画出奈氏曲线,并且能根据积分环节个数能正确修正,能正确的计算出正负穿越次数.
[1] 陈振东.基于频率域的显著性区域提取方法[J].枣庄学院学报,2012,29(5):129-134.
[2] 熊新民.自动控制原理与系统[M].北京:电子工业出版社,2003.
[3] 刘祖润.自动控制原理[M].北京:机械工业出版社,2000.
[4] 孙振川.基于s函数的异步电动机在两相静止坐标系下的仿真建模[J].枣庄学院学报,2012,29(5):82-84.

