一种改进的GNSS/INS非相干深组合导航
金东阳,刘党辉,夏长峰
(装备学院,北京 怀柔 101416)
0 引 言
现有的GNSS/INS组合导航主要分为松组合、紧组合与深组合。从辅助方式上来说,松组合与紧组合是单方面的对INS进行辅助,一旦接收机在强干扰、卫星信号中断等恶劣条件下无法工作,组合导航系统将陷入瘫痪。深组合在结构上是一种接收机与INS互辅助的组合方式,INS的导航结果经过接收机校正后,继续辅助接收机内部跟踪过程,有效提高了系统在恶劣环境下的精度。
深组合导航经过近年来发展,逐步产生了两大类:相干深组合与非相干深组合[1]。在相干深组合中,接收机将每一通道内的I、Q支路信号集中直接作为导航滤波器观测量,对INS误差信息进行估计。Edwards 等[2]采用这种结构,利用FPGA硬件平台,有效解决了在弱信号环境中深组合导航的定位问题。Jwo 等[3]对这种集中式的相干深组合进行仿真,其导航滤波器中分别应用扩展卡尔曼滤波、无迹卡尔曼滤波、多模交互式扩展卡尔曼滤波、多模交互式无迹卡尔曼滤波四种算法,对比不同算法的导航精度与实时性,实验表明:采用多模交互式无极卡尔曼滤波算法时,系统在高动态环境性能最优。但是,这种集中的相干式深组合导航滤波维数巨大,如Draper实验室采用了一个 42 维的集中滤波器,这导致其计算负担过重,系统实时性差,不适合工程上进一步应用[4]。
非相干深组合导航在设计上保留了接收机原有的码鉴相器与载波相位鉴别器等模块,利用通道滤波器对接收机需要的跟踪信息进行估计,取代了传统接收机跟踪环路低通滤波器等结构,同时避免了相干式深组合结构带来的运算负担大等问题[5]。非相干深组合导航通道滤波器通常以信号幅度、码相位误差、初始载波相位误差以及载波频率误差为状态变量[6]。但是信号幅度作为状态变量对于接收机跟踪过程并不是必要的,在通道滤波器中由于引入信号幅度状态变量不但增加了算法的复杂程度,而且会带来更多的观测噪声,为进一步提高导航精度,本文针对通道滤波器算法提出改进。
1 非相干深组合导航原理
图1中所展示的是某一通道内部的具体结构,系统由接收机基带信号处理模块、通道滤波器模块、INS解算模块、导航滤波器模块共同组成。
非相干深组合利用码与载波鉴相器与通道滤波器对码相位误差、载波相位误差、载波频率误差进行估计,对码NCO与载波NCO进行控制,并计算接收机与导航卫星的伪距与伪距率信息。与此同时,INS实时解算在ECEF坐标下,载体的位置、速度等信息,根据接收机导航电文支路所解调的卫星星历,计算INS测出的伪距与伪距率信息。INS与接收机所估算的伪距、伪距率的差值作为导航滤波器的观测量,再通过导航滤波器估算出INS误差状态值与接收机跟踪环路内部跟踪误差修正量。INS误差状态值用于校正INS系统所输出的导航信息。非相干深组合导航系统的最终导航信息由经过校正的INS输出。
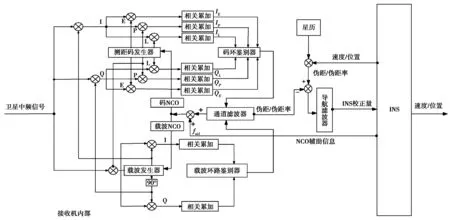
图1 非相干深组合导航原理图
传统接收机跟踪方式主要以标量跟踪为主[7],当卫星信号信噪比变化时,由于跟踪环路中采用低通滤波器,其增益与带宽固定,标量跟踪方式无法适应这种变化,信号质量下降严重时,会最终导致跟踪失锁,非相干深组合采用矢量跟踪环路有效避免了上述问题。
2 矢量跟踪环路
矢量跟踪环路中经过积分的I、Q支路信号,分别在码延迟锁定环路与载波跟踪环路进入各自的鉴别器中,鉴别器输出量作为通道滤波器的观测值,通道滤波器模块的功能是利用观测量,基于Kalman 滤波算法,对码相位误差、载波相位误差、载波频率误差进行估计,其估计结果与导航滤波器所反馈的辅助频率对码NCO与载波NCO进行控制,形成闭合的跟踪环路,如前文诉述,矢量跟踪环路的核心在于通道滤波器的设计。
2.1 通道滤波器设计

其中:a0,δa0,δf0,δθ0,δτ0各状态变量是Kalman滤波之前的初始值;β为弧度-码片转换因子,且β=λL/2πλCA.


(1)
观测量取第k次积分时间ΔT内本地载波鉴相器输出Δθ与码鉴相器输出Δτ,则观测方程可表示为

(2)
2.2 INS辅助跟踪原理
深组合与紧组合的重要区别在于,深组合是一种INS与接收机相互辅助的组合导航结构,对于无辅助的接收机PLL跟踪环路,其反馈量仅能从自身通道中获得,在深组合结构中,PLL的NCO同时接受导航滤波器控制。INS辅助载波跟踪环路,即将通过卫星星历中包含的卫星速度和INS中包含的载体速度求得的多普勒频率引入到跟踪环路中,减弱或消除载体的动态,同时又能使环路噪声带宽大大减小,提高接收机的抗干扰性。利用经过校正后的INS输出的速度辅助估计跟踪环路多普勒频率,可有效降低PLL动态范围,在跟踪过程中,通过减小带宽,可同时实现消除动态影响与提高抗噪能力,如果卫星信号发生中断,INS可持续估算载体的多普勒频率误差,保持卫星信号不失锁。

(3)
式中:Li表示视线方向接收机与卫星的单位矢量,Vaid表示辅助速度,则有
(4)
式中:faid为INS辅助多普勒频率;fL为北斗卫星信号载波频率;c为光速。
2.3 NCO控制方法
通道内NCO控制量计算公式为

(5)

2.4 导航滤波器
导航滤波器模型与紧组合导航滤波器模型相类似,可以表示为
(6)
式中:XI(t)=[δL,δλ,δh,δVe,δVn,δVu,φe,φn,φu,εe,εn,εu,e,n,u];XG=[δtu,δtru];δL,δλ,δh表示在东北天坐标系下INS的位置误差;δVe,δVn,δVu表示东北天三向速度误差;φe,φn,φu表示姿态角误差;εe,εn,εu为陀螺仪常值漂移;e,n,u为加速度计零偏;δtu与δtru分别表示接收机钟差与钟频误差;W(t)为系统噪声。


(7)
式中,VGNSS为观测噪声,其中具体状态矩阵FI,FG以及噪声状态矩阵GI,GG与观测矩阵H的取值参考文献[10]。
3 仿真实验分析
以东北天坐标系为导航坐标系,仿真惯性元件信号误差:陀螺仪常值漂移0.3°/h,白噪声均方差0.02°/h,加速度计常值零偏为100 μg,白噪声均方差为10 μg.针对卫星仿真信号,接收机预检测积分时间为 1 ms,采样频率为 30 MHz,采样后信号中频为 7 MHz.紧组合中跟踪环带宽为 10 Hz,设定阻尼因子为 0.707,码环为二阶延迟锁定环,噪声带宽为2.5 Hz,载波环和码环增益分别为 0.3 和 0.5,信噪比约为-20 dB.为验证本文所设计的非相干深组合导航跟踪性能,分别仿真环路无INS辅助跟踪的紧组合,跟踪环路采用传统通道滤波器的非相干深组合,与本文所设计的非相干深组合导航,对比同一通道紧组合多普勒频率误差与非相干深组合多普率频率误差的跟踪情况。
3.1 改进的通道滤波器性能
图2示出了紧组合、采用传统通道滤波器模型的非相干深组合与采用本文改进的通道滤波器模型非相干深组合某一通道内的多普勒频率误差对比。由图可知紧组合在起始跟踪时,通道内多普勒频率误差波动较大,跟踪所需时间较长。由于改进的通道滤波器中状态变量减少了信号幅度,同时增加了载波相位变化率加速度误差,相比于传统通道滤波器含有噪声较少,这将使环路跟踪过程更为精确。

图2 通道跟踪性能对比
图3示出了紧组合、采用传统通道滤波器模型的非相干深组合、采用改进的通道滤波器模型的非相干深组合所解调的导航电文,从解调出的信号质量可以看出,紧组合与传统通道滤波器所解调出的导航电文质量较差,传统通道滤波器相比于紧组合解调效果稍有提高,改进的通道滤波器所解调出的导航电文中误差较小,信号质量较前两种方法有明显提高,说明改进的通道滤波器到滤波器跟踪性能更加优越,有效降低了导航电文的误码概率,与前文分析一致。

图3 解调导航电文效果对比
3.2 改进的非相干深组合导航性能
图4、图5分别示出了紧组合、传统的非相干深组合导航与改进的非相干深组合导航东向、北向的位置误差与速度误差。从图中可以看出,紧组合导航精度明显不及非相干深组合,在所设的仿真条件下,改进后的非相干深组合精度较传统方法有了进一步提升,收敛后的位置误差在2 m级左右,速度误差不超过0.2 m/s,且收敛速度较快,说明这种改进的非相干深组合导航可以进一步提高系统的导航精度。

图4 东向位置速度误差


图5 北向位置速度误差
4 结束语
在利用传统通道滤波器模型中,由于码与载波鉴相器不含有信号幅度的估测信息,导致跟踪环路中观测噪声较大,本文提出将通道滤波器模型进行改进,去除信号幅度状态变量,同时加入载波相位变化率加速度误差,仿真实验表明:这种改进的非相干深组合导航方法的跟踪性能与导航精度相比于传统的非相干深组合导航方法有了进一步提高。
[1]王新龙,于 洁. 基于矢量跟踪的 SINS/GPS 深组合导航方法[J]. 中国惯性技术学报,2009,17(6): 710-717.
[2]EDWARDS W L,CLARKl B J,BEVLY D M. Implementation details of a deeply integrated GPS/INS software receiver[J]. IEEE,Position Location and Navigation Symposium (PLANS),2010:1137-1146.
[3]JWO Dahjing,HU Chiawei,TSENG Chienhao. Nonlinear filtering with IMM algorithm for ultra-tight GPS/INS integration[J]. International Journal of Advanced Robotic Systems,2013,10(222):1013-1029.
[4]文 立. 基于环路卡尔曼估计的惯性/GPS 深组合算法研究[D]. 南京:南京航空航天大学,2011.
[5]GRONES P D,MATHER C J,MACAULAY A . Demonstration of non-coherent deep INS/GPS integration for optimized signal-to-noise performance[J]. Proceedings of the Institute of Navigation (ION GNSS 2007),2007: 2627-2638.
[6]PETOVELLO M,LACHAPELLE G. Comparison of vector-based software receiver implementations with application to ultra-tight GPS/INS integration[C]// Institute of Navigation GPS/GNSS Conference. Fort Worth,TX. Institute of Navigation,2006:1790-1799.
[7]ZHAO S,LU M,FENG Z. Implementation and performance assessment of a vector tracking method based on a software GPS receiver[J]. Journal of Navigation,2011,64(S1): 151-161.
[8]MESKIN D G,BAR-ITZHACK I Y. Observability analysis of piece-wise constant systems-part i:Theory. [J].IEEE Transactions on Aerospace and Electronic System,1992,28(4): 1056-1067.
[9]WON J H,DOTTERBOCK D,EISSFELLER B. Performance comparison of different forms of Kalman filter approaches for a vector-based GNSS signal tracking loop[J]. Navigation,2010(57):185-199.
[10]张光理. 北斗/SINS 组合导航系统研究[D]. 哈尔滨:哈尔滨工程大学,2012.

