基于马尔科夫链的公交站间行程时间预测算法*
胡继华 李国源 程智锋
(1.中山大学工学院 广州市510006;2.广东省智能交通系统重点实验室 广州510006)
0 引 言
优先发展公交系统是提高城市交通资源利用效率,缓解交通拥堵的重要手段。城市公交行程时间具有明显的时段分布特征,尤其是早晚高峰与平峰时段的公交行程时间各不相同,导致公交到站时间间隔不均匀、可靠性下降、候车时间过长、载客率差异大等诸多问题,影响了乘客乘坐公交的意愿[1]。研究公交车辆行程时间预测方法,对于提高公交车辆时间可靠性、公交车辆调度、提高公交资源利用率及吸引人群采用公交出行等具有重要意义。
公交车辆行程时间预测方法包括历史趋势方法预测、多元回归法预测模型、人工神经网络模型、卡尔曼滤波模型、非参数回归模型预测方法及支持向量机模型等。
基于历史数据的预测模型是通过对同一时段的大量历史数据取平均值进行预测,其预测精度较低,但算法及校正简单,实际应用广泛。陈巳康等[2]通过研究公交车路段平均运行速度来确定路段行程时间。
回归模型研究-系列自变量与因变量之间的关系。周雪梅等[3]提出了多元回归公交行程时间分析预测模型,并利用威海市的公交数据对该分析预测模型进行验证。魏华等[4]通过研究公交行程时间与道路路段实时交通量的关系,从而确定预测模型。
人工神经网络是由大量的节点(神经元)及其之间的相互联接构成的1种运算模型。相对于回归模型,神经网络算法不需要考虑输入变量之间的关系,也不需要特定的方程式。杨兆升等[5]提出了1种基于模糊神经网络的实时路段行程时间估计模型,该模型可利用实测交通数据实时预测未来路段公交车辆行程时间。Ehsan等[6]将道路饱和率和公交时刻表准点率作为输入变量,其预测精度高于历史数据模型。神经网络普遍存在学习过程、算法的时间耗费过多,导致实时预测的效率低下。
卡尔曼滤波模型是1种基于线性递归的算法,由于其高效的预测误差修正特性,该算法在动态预测中有一定的应用。美国的Mei Chen等[7]利用了AVL数据建立了公交车到达时间的卡尔曼滤波预测模型。国内的周文霞[8]等考虑多种影响因素,利用卡尔曼滤波算法给出了行程时间预测模型。
机器学习中的支持向量机也逐渐在公交行程时间预测中得到应用。Peng等[9]提出了基于贝叶斯概率的相关向量机预测算法,可获取到站时间预测值及误差的方差。Yu等[10-11]将支持向量机应用到公交行程时间预测中,该预测模型具备更强的解释力及稳定性;并且将遗忘因子引入到支持向量机预测模型中,得到了更高的预测精度。
交通流信息反映道路的实际交通情况,故能在此基础上预测公交行程时间。2012年李海姣等[12]以交通波理论为基础建立了站点间行程时间预测模型,取得较好的预测效果。
马尔科夫链在交通领域方面的应用主要集中在交通事故[13]、交通流密度[14]等方面,在公交行程时间预测的应用还较少。马尔科夫链预测针对状态转移进行计算[15],具有可操作性较强,且简单的特点。笔者研究基于马尔科夫链的公交站间行程时间预测算法,并利用移动误差补偿法对其进行改进以得到更高的预测精度。
1 基于马尔科夫链的预测算法
1.1 算法基础
公交车辆是1类时空过程对象,其在特定的线路运行过程中受到当时具体的环境影响,包括道路交通状态、车辆运行状况及天气状况等多种因素。在1次过程中,公交车辆下一阶段的运行过程受到前一阶段或多个阶段的运行状况影响较大,比如,为了保证班次准点,当车辆在前面的站点发生延误时,车辆在后续站点会相应加速以弥补延误时间。
公交车辆行程时间是由各个站间行程时间及停站时间构成,且站间行程时间的预测是动态行程时间预测的关键。某一站间行程时间可视为特定公交线路的系统状态,一系列的站间行程时间是系统在不同阶段的运行状态,因此可以利用离散系统的预测方法来估计公交车辆站间行程时间。
公交车辆是典型的时空过程对象,其运行具有状态转移性,公交车辆的下一阶段发生状态的概率与当前状态相关,符合马尔科夫链的基本思想,因此提出以下假设。
假设1。同一线路同一方向下的公交车辆站间行程时间的延误符合马尔科夫过程。
假设2。同一线路同一方向在同一时段内,所有的站间状态转移概率一致。
在假设1的前提下,实际上是公交车辆站间行程时间的延误构成了马尔科夫链,因此只需要预测公交车站行程时间的延误,即可得到公交车辆站间预测行程时间;假设2充分考虑了公交车辆运行的时段差异特征,同时,认为同一时段同一方向的公交运行具有同质性,简化了马尔科夫状态转移矩阵的复杂性。
1.2 基本算法
对于一系列相依的随机变量用步长为1的马尔科夫链模型和初始分布推算出未来的绝对分布,即为基于马尔科夫链的基本行程时间预测算法,具体预测算法步骤如下。
1)划分车辆运行时段。对1 d内的公交车辆工作时间进行时段划分,假设1 h为1个时段Ti,那么07:00时到19:00时则可划分为12个运行时段。
2)构造状态转移矩阵。状态转移矩阵依赖于公交车辆运行的历史数据,对于每个运行时段,对要预测的线路统计3个相邻公交站点a,b,c之间的站间运行时间tab和tbc,见图1。
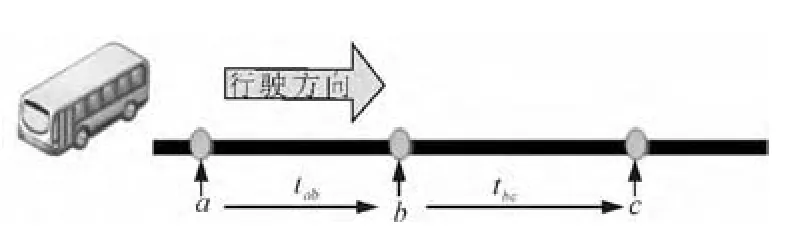
图1 公交行驶图示1Fig.1 Schematic Illustration 1 of bus driving
则得到公交车辆的站间延误为
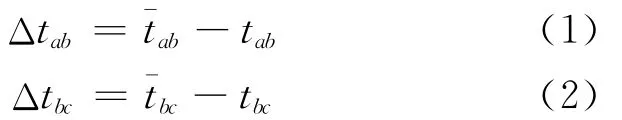
(Δtab,Δtbc)构成了一系列的延误转移对,如(-20,-10)表明在(a,b)站间的延误由-20s转变为(b,c)站间的-10s,并且可以得到(-20,-10)此状态转移发生的概率。由一系列的延误转移对得到1个在时段T线路R的延误转移概率矩阵。
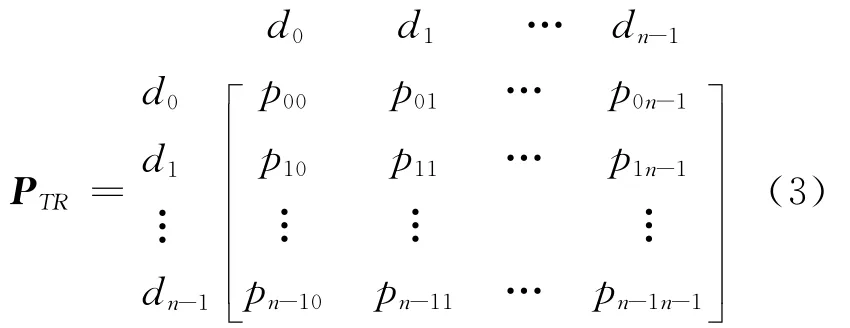
式中:di或dj(i,j∈ [0,n-1])是具体的延误时间,正数表示公交车辆提前到站,负数表示延迟到站,且满足为简化转移概率矩阵,可以将dij转化为连续的时间范围值。
3)马氏性检验。马氏性的检验,是决定序列是否可用马尔科夫链预测方法来预测的关键,只有公交车辆站间行程时间延误序列符合马氏性检测条件,才能用马尔科夫链进行预测。验证马氏性一般用卡方检验方法[16]。
4)站间行程时间动态推导:已知线路R的某辆公交车在时段T内,在(b,c)站间的运行延误时间为Δt′bc,见图2:
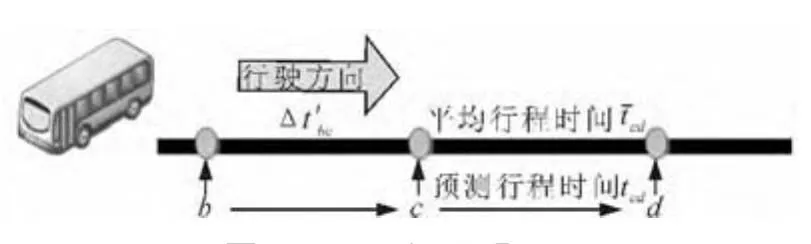
图2 公交行驶图示2Fig.2 Schematic Illustration 2 of bus driving
即其在(c,d)站间的预测行程时间tcd为
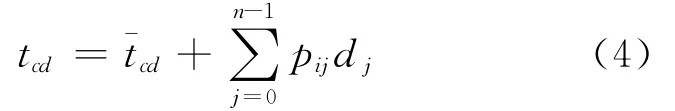
式中:pij=PTR(i,j)。
根据上述可见,首先由 Δt′bc确定di,找到Δt′bc在状态转移概率矩阵PTR中的行,然后求解该行概率下的转移概率期望,即可得到该站与下一站的公交车辆站间的预测行程时间延误,进而得到站间的预测行程时间。
1.3 改进算法
直接由概率矩阵得到的预测值在平稳序列中的鲁棒性较大,但当公交线路行驶阶段不稳定状态较多时,马尔科夫预测值的失真度也较大,造成马尔科夫链算法预测不准确的假象。因此,提出了1种移动误差补偿法,提升预测精度。
改进算法的基本思想是假设在公交车辆运行过程中,上一状态的预测误差与下一状态的预测误差具有较高的相似性,即用已知的预测误差减少当前预测时间的误差。具体描述如下。
1)假设到达公交车站K时得到的马尔科夫预测站间行程时间为tK,而实际的站间行程时间为则称实际站间行程时间与预测站间行程时间tK的差值为公交车站K的移动误差,即

上式为单步的移动误差;K步的移动误差为
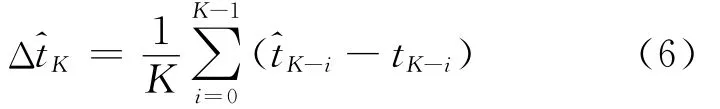
2)当城市道路上有突发事件发生时,实际的公交车辆站间行程时间会大幅度增加,带来极端的移动误差。为了消除极端移动误差,在此引入移动误差阈值θ,因此可将K步移动误差公式改
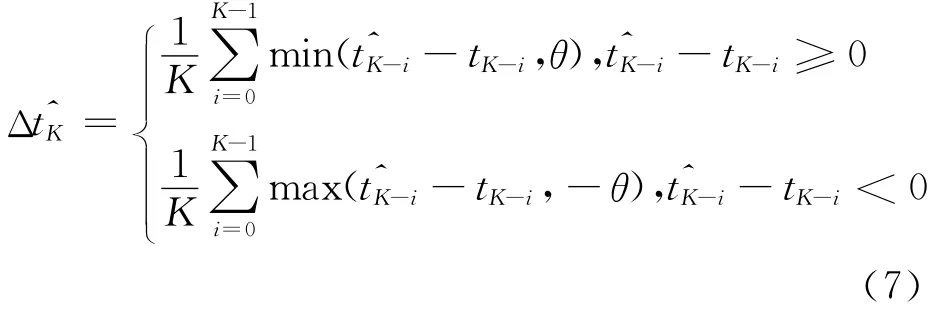
写为式中:移动误差阈值θ为样本数据中站间实际行程时间与平均行程时间之差的绝对值的平均值。
3)当预测公交车站K与下一站K+1的站间行程时间时,将多步的移动误差补偿到马尔科夫预测值中,得到的站间行程时间预测值为
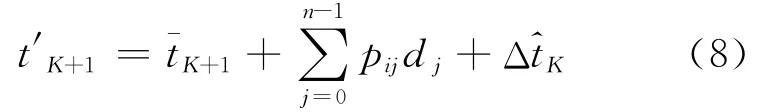
上式中前2项与基本算法的预测公式一致,为直接由状态转移概率矩阵得到的预测站间行程时间值。由引入阈值的移动误差则可以不断将前K个状态的预测误差补偿到下一状态的预测中。在公交车辆的1次行程中,前面几个站点的数量可能满足不了K个状态的预测误差补偿,则以最大步长作为补偿差,比如到达第3个站台后要预测到达第4个站台的行程时间,最大只能用2步的移动误差补偿。
2 实例验证
2.1 实例数据集
为了评估该算法的预测性能,使用了广州市BRT线路B1自2011年8月22日~28日共1周的GPS数据进行实验。首先由GPS数据得到状态转移概率矩阵,然后提取20个完整的公交线路行驶过程进行预测仿真。
原始GPS数据给出的是时间和经纬度信息,需要对公交站台进行匹配和车辆状态分析,通过划分得到公交车辆进站出站的过程。其数据结构见表1,平均每个时段可以获得483个转移序列对。
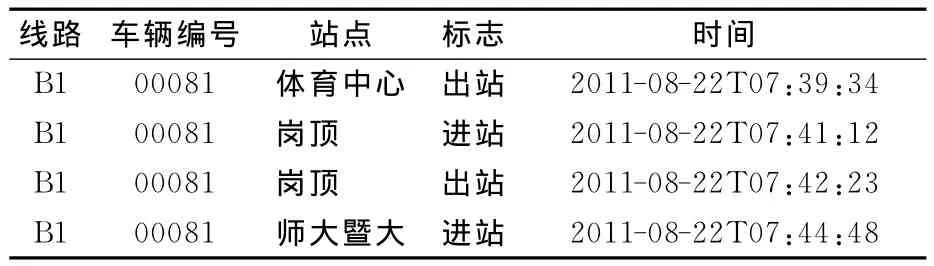
表1公交车辆GPS数据集数据结构表Tab.1 Structural table of GPS data for the public vehicles
2.2 马氏性检验
采用卡方检验方法来检验随机过程{Xt,t∈T}是否具有马氏性,根据上述统计估算法得到公交车辆站间行程时间延误转移频数矩阵,进而由转移频数矩阵和公式计算,可得

即有χ2=599.698 8。
令自由度为k=(m-1)2=(15-1)2,即k=196,此处取置信度α=0.01。由于k>45,χ2α(k)不能直接查表得到,当k值足够大时,有
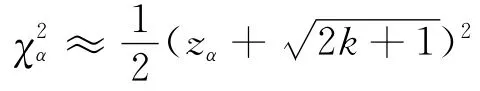
式中:zα为标准正态分布的上α分位点。查表得到z0.01=2.235,则可得到可即该随机过程为马尔科夫过程。
同理对剩余划分时段的值进行计算,均有χ2,即对于各研究时段,其随机过程符合马氏性,也即所建立的模型为马尔科夫模型。
2.3 评价指标
为了评估和比较各个公交站间行程时间预测模型的预测精度,从而引入平均绝对相对误差εM(mean relative percentage error,MRPE)和均等系数εE(equality coefficient,EC)2个指标,二者的定义分别为
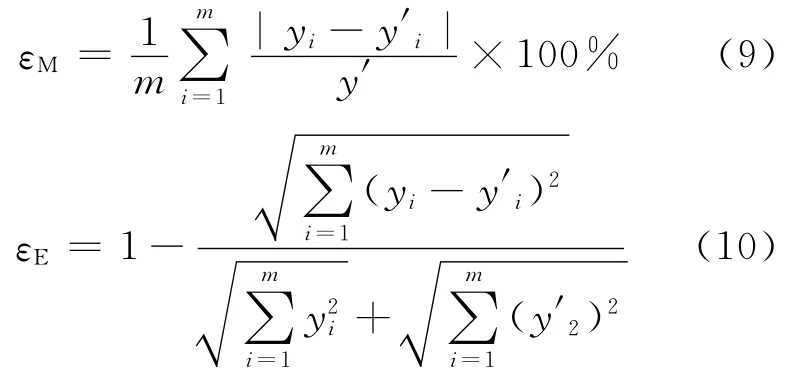
式中:m为单程所要预测的站间行程数,y′i为第i段行程的实测值,yi为第i段行程的预测值。εM表征了单程中预测值和实测值的平均绝对相关误差,εM越小,表明预测精度越高;εE表征了单程中预测值对于实测值的偏离程度,εE越大,表明预测精度的稳定性越高。
2.4 模型对比
为了检验预测算法的精度,除了将预测算法的结果与实际数据进行比较分析之外,实验采用了BP神经网络作为对比预测算法。算法如下。
1)建立1个3层的BP神经网络,其中输入层共有5个神经元,分别输入时段T下前3 d各自的站间平均行程时间,该时段总的站间平均时间和上一状态的站间行程时间。
2)中间层神经元的数目采用经验公式

式中:n为输入层神经元数量,所以中间层的数量为3。神经元激励函数使用常用的Sigmoid函数,其数学形式为
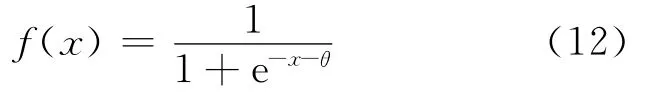
3)神经网络的输出层为1个神经元,输出所要预测的站间行程时间。训练样本同样为B1的1周GPS数据,确保了预测效果对比的可信性。
2.5 预测结果与分析
分别计算20次实验中基本马尔科夫算法、BP神经网络以及马尔科夫改进算法的平均绝对相对误差和均等系数,具体结果值见图3、4。由图3可知,马尔科夫改进算法的平均绝对相对误差总体偏低,基本马尔科夫算法次之,对比模型BP算法最高。而由图4可知,马尔科夫改进算法的均等系数整体偏高,说明其预测稳定性最高;同时,3种算法各自的评价指标的平均值见表2。可以看出马尔科夫改进算法的平均MAPE最小,说明预测误差小,平均EC最大,说明其预测稳定性高。因此,从总体来看,马尔科夫改进算法在公交行程时间预测中更优,预测准确性和稳定性都较高,基本马尔可夫算法次之。
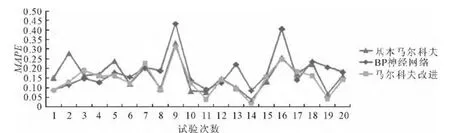
图3 MAPE对比曲线Fig.3 Comparison curve of MAPE
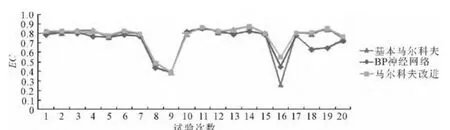
图4 EC对比曲线Fig.4 Comparison curve of EC

表2 评价指标平均值Tab.2 Average value of evaluation indicator
图5为随机抽取的4次实验中公交站间行程时间的实测值和预测值对比示意图。从图5中可以看到,马尔科夫改进算法的公交站间行程时间预测结果较其他2种算法更加接近实测值。
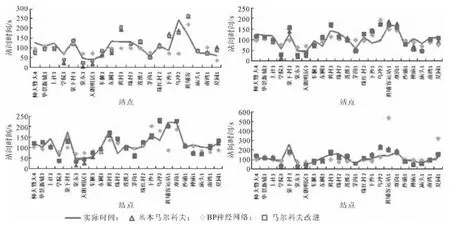
图5 实际值与预测值对比图Fig.5 Comparison curve between actual value and predicted value
3 结束语
针对公交车辆的运行特性,提出了基于马尔科夫链的公交站间行程时间预测及其改进算法。笔者首先将公交车辆在站间的运行过程视作马尔科夫链,由GPS数据提取出不同时段下站间行程时间的马尔科夫状态转移矩阵,实现了站间行程时间的动态推导;然后提出了移动误差补偿法对原有的马尔科夫预测算法进行了改进,以得到更高的预测精度。
最后,笔者以广州市BRT线路B1的实际运行GPS数据,通过基本马尔科夫算法及BP神经网络算法对改进算法进行了验证。实验结果表明,引入移动误差补偿法对基本马尔科夫算法进行改进后,公交站间行程时间预测精度和稳定性均有所提高,效果更佳。
下一步的工作目标是探究提出多组合模型算法,进一步提高预测精度和稳定性。
[1] 彭昌溆,周雪梅,张道智,等.基于乘客感知的公交服务质量影响因素分析[J].交通信息与安全,2013,31(4):40-44.
[2] 周雪梅,杨晓光,王 磊.公交车辆行程时间预测方法[J].交通与计算机,2002(6):12-14.
[3] 魏 华,贾守镇.公交车辆实时动态行程时间与行车间隔确定方法研究[J].渭南师范学院学报,2005(13):8-10.
[4] 韩 印,杨兆升,胡坚明.公共交通智能化调度基础数据预测方法研究[J].公路交通科技,2003,6(3):140-143.
[5] Ehsan Mazloumi,Sara Moridpour,Grahan Currie,et al.Exploring the value of traffic flow data in bus travel time prediction[J].Journal of Transportation Engineering,2012(138):436-446.
[6] Chen Mei,Liu Xiaobo,Xia Jingxin.A dynamic bus-arrival time prediction model based on APC data[J].Computer-Aided Civil and Infrastructure Engineering.2004(19):364-376.
[7] 周文霞,徐建闽,刘正东.基于卡尔曼滤波算法的公交车辆行程时间预测[J].交通标准化,2007(2):174-177.
[8] Peng Chen,Yan Xinping,Li Xuhong.Bus travel time prediction based on relevance vector machine[C]∥Information Engineering and Computer Science,2009.ICIECS 2009.International Conference on.Wuhan:Wuhan University,2009:1-4.
[9] Yu B,Yang Z Z,Wang J.Bus travel-time prediction based on bus speed[J].Proceedings of the Institution of Civil Engineers-Transport,2010,163(1):3-7.
[10] Yu B,Ye T,Tian X M,et al.Bus travel-time prediction with forgetting factor[J].Journal of Computing in Civil Engineering,2012.
[11] Chung Y S,Kim J M,Kim D H,et al.A study to prediction modeling of the number of traffic accidents[M].Multimedia and Ubiquitous Engineering.Berlin:Springer Netherlands,2013.
[12] 李海姣,陆 建.基于交通流理论的公交站点间行程时间预测[J].交通信息与安全,2012,30(3):29-32.
[13] Hillier F S,Lieberman G J,胡运权.运筹学导论[M].北京:清华大学出版社,2007:714-746.
[14] 冯耀龙,韩文秀.权马尔科夫链在河流丰枯状况预测中的应用[J].系统工程理论与实践,1999,10(10):89-98.
[15] 张 鑫,任永泰,王福林.基于改进灰色马尔科夫模型的年降水量预测[J].数学的实践与认识,2011,6(11):51-56.
[16] 雷宗光,张 君.基于马尔科夫链模型的沪深300指数日收益率研究[J].科技创业月刊,2007,20(9):35-36.

