慢行交通衔接轨道交通换乘时间分析

劳春江 刘国贵

(重庆交通大学交通运输学院，重庆 400000)

慢行交通是指速度低于20 km/h、以人为本、注重公平、可持续发展的近距离出行交通方式的统称［1］。在此把步行、自行车交通方式作为考虑的对象。轨道交通是满足城市交通快速发展的需要，大容量的轨道交通可以大大减少其他交通方式的压力，是城市公共交通的重要组成部分。但轨道交通本身并不能直接提供“点对点”的服务，而慢行交通主要是用于短距出行，两者之间存在较强互补性。而完善的步行系统和自行车路网在方便了非机动化交通出行的同时也提高了轨道系统的可达性，因此应着力发展“自行车+轨道”及“步行+轨道”的换乘模式，促进两者协调发展。当前轨道交通与慢行交通网络一般相互独立，在初期的规划以及后者的运营中，没有形成一体化的衔接。轨道站点内的设施规模不足、轨道列车的发车频率安排不合理等因素致使乘客的排队服务时间与候车时间过长，降低轨道交通的服务水平，导致达不到预测客流量水平，影响轨道交通经济效益，运营的质量难于得到保证。

从总体上看，在轨道交通规划过程中考虑轨道交通与其他交通方式衔接问题时，主要是对两者换乘系统在总体布局上进行分析，且大多关注换乘枢纽与线网规划的设计问题，在运营过程中没有充分考虑轨道交通与慢行交通的协调。在此主要考虑在靠近城市中心区，以“步行+公交”模式换乘;对于外围区，则以“自行车+公交”模式换乘。分析乘客通过轨道交通的换乘时间问题，对换乘设施优化调整，进行列车时刻表的协调，减少换乘时间。

1 进站乘客换乘时间分析

乘客换乘目的轨道站点，换乘时间上存在一定的延误。这里基于合理的慢行交通系统布局基础上，换乘设施和换乘服务水平对换乘延误时间产生较大影响。换乘设施主要包括轨道站内售票窗口和进出站检票口排队类设施、换乘通道、换乘楼梯和自动扶梯集散设施。服务水平主要包括换乘线路列车时刻的设计，如列车间隔、列车间隔时间、到发时间的匹配协调，以及发布相关信息等产生出行者的等待时间。缩短乘客的换乘延误时间，可以减少乘客换乘时间，使乘客换乘时间最短的目标得到实现。

乘客换乘时间主要包括四部分，即t=t1+t2+t3+t4，其中，t1为乘客步行/自行车到达轨道站点/自行车停靠点所用的时间;t2为购票检票时间;t3为乘客在集散设施的步行时间;t4为乘客在轨道站点的候车时间。

慢行交通系统布局设计关系到乘客到达慢行交通换乘点所用时间t1。这里是基于慢行交通设施布局合理的情况下，轨道站点对步行乘客的辐射范围一般为500 m～800 m，以正常步行速度1.2 m/s，乘客到达轨道站点的时间为0 min～7 min或0 min～11 min;而轨道站点对自行车乘客的辐射范围一般是1 000 m～2 000 m，以普遍的自行车速度2.8 m/s，自行车乘客到达轨道站停靠点的时间为0 min～6 min或0 min～12 min，轨道站点对步行/自行车乘客的辐射半径内，可把乘客到达站点的换乘时间视为固定值。

排队类设施服务台的数量及其服务能力影响乘客购票检票时间t2，在车站内乘客在设施服务台前排队容易发生拥挤，因此车站的集散能力、乘客的排队时间与排队类设施服务台的数量有关，合理配置服务台的数量对提高公共交通的服务水平具有重要的作用。

乘客在集散设施的平均步行时间t3主要与换乘通道的长度有关，在同一换乘通道的情况下，步行速度一般取1 m/s，因此把步行时间t3视为固定值考虑。

下面对t4产生的三种情况分别进行分析:乘客到达时间与轨道列车时刻表的衔接会影响乘客的候车时间t4。1)乘客到达轨道站台时，列车还没有到站，乘客需要等待一定时间，这时候车时间t4小于列车的发车间隔;2)乘客到达轨道站台时，列车刚好离开站点，这时乘客的候车时间最长，乘客的等待时间为一个发车间隔;3)乘客到达轨道站台时，列车刚好到站，这种情况下乘客候车等待时间为零。

由以上分析得知，乘客购票检票时间和换乘候车时间对换乘轨道交通的时间产生主要影响。缩短乘客在设施前的排队时间以及换乘候车时间可以大大缩短乘客换乘时间。针对上述问题，可以通过合理确定排队类设施服务台的数量，在运营中进行列车时刻表的协调和优化，缩短换乘等待时间，使慢行交通与轨道交通的衔接效率得到提高。

2 售检票排队设施等待时间模型

排队设施服务台数量、设施所服务客流的平均到达率γ、每个服务台的平均服务效率μ等因素都会影响乘客的排队时间。乘客在设施服务台前排队可以视为一个排队论系统，因此可以用排队论中相关方法来建立排队等待时间模型。

乘客其平均到达率为γ，符合泊松分布，并假设γ为已知值，服务台的平均服务效率为μ，可根据设施的通过能力得到。设服务台的总数为c。系统中乘客的平均排队长度L=(γ/c)2/［μ·(μ－γ/c)］，排队中的平均等待时间为:

3 乘客候车等待时间模型

在运营中，对车辆调度时，要考虑换乘时间中乘客等待时间，尽可能地缩短乘客换乘等待时间。在平峰时，等待候车的乘客全部能换乘成功，而高峰时只有一部分乘客换乘成功，另一部分乘客需要等待下一班列车。因此对平峰期间与高峰期间这两种情况分别进行探讨。这里设高峰期间发车间隔为T高，平峰期间发车间隔为T平，发车间隔为固定值。

3.1 平峰期间

交通平峰期间，候车的乘客全部都能换乘成功，无需等待下一班列车。平峰期间分别对城市中心区和外围区的轨道站点的候车时间进行分析。假设在城市中心区站点以及枢纽站，客流量较多，乘客在候车时形成排队，而外围片区站点客流较少，无需排队等候。

3.1.1 城市中心区站点乘客候车时间

假设城市中心区乘客的到达近似泊松分布，各站到达率为λi，列车各站点能够上车人数为Pi，故服务率 φ=Pi/T平，列车门看成2个可服务的通道，则每个服务通道的平均服务效率φ1=φ/2N，N为列车门的数量，这时列车与到达客流构成了“单路排队多通道服务系统”。站点中乘客的平均排队长度为2N)2/［φ1·(φ1－ λ1/2N)］，这时轨道站点 i处乘客平峰期间平均候车时间为:

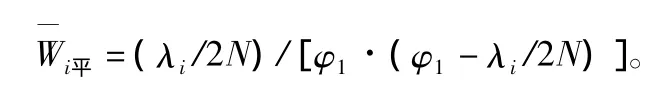
3.1.2 城市外围站点乘客候车时间

外围站点乘客的到达服从泊松分布，平均到达率σi，乘客平均时间间隔为1/σi，这里并假设第一个候车乘客到达时，与上一列车离站相隔Δt，于是这位乘客的候车时间为(T平－Δt)，接下来一位乘客的候车时间为(T平－Δt－1/σi)，则第j名乘客的候车时间为［T平－Δt－(j－1)/σi］，乘客总候车时间为:

一个发车间隔T平内，总共可以到达的人数为:

乘客平均候车时间为:

3.2 高峰期间

交通在高峰期间，因为上下学、上下班的客流量较多，导致慢行交通乘客到达轨道交通点后形成过长的排队。由于列车载客量的限制，排队中乘客不能完全成功换乘，有一部分乘客不得不等待下一班列车，导致增加了延误时间。

对于站点i，乘客到达率为γi，发车时间间隔T高内，排队的乘客数为γi·T高，故服务率φ高=Pi/T高，把列车门看成可服务的2个通道，则每个服务通道的平均服务效率φ2=φ高/2N，换乘成功的Pi名乘客平均等待时间为=(γi/2N)/［φ2·(φ2－ γi/2N)］，排队中有γi·T高－Pi人不得不等待下一辆列车。高峰期间乘客在轨道站i点处平均候车时间为:

4 换乘时间评价

换乘时间主要与步行距离、换乘客流量、检票口的通过能力以及售票窗口的服务水平、轨道运输能力等因素相关，因此相对应地提出将换乘步行通道时间I、售检票设施排队时间T、候车等待时间W作为换乘时间的评价指标。将换乘时间用换乘损失U来衡量:

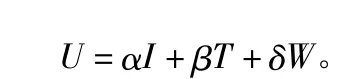
其中，α，β，δ分别为乘步行通道时间I、售检票设施排队时间T、候车等待时间W的权重。权系数的确定可采用专家法、特征向量法等。一般乘客等待时间不要超过10 min，早晚高峰时一般不超过5 min［4］。对换乘时间的定量研究为研究换乘对出行需求的影响提供条件，从而有助于改进各影响因素，缩短乘客换乘时间，进而提高换乘的无缝衔接性。

5 结语

换乘时间是反映慢行交通与轨道交通系统衔接效率的定量指标，它可以对衔接换乘布局、运营模式进行评价。对慢行交通衔接城市轨道交通的换乘时间分析问题进行了研究，在研究中运用排队论模型，建立乘客换乘时间模型，并提出评价方法。其研究成果是为确定换乘站设施规模与轨道列车发车间隔提供依据，提高了公共交通服务水平和公共交通吸引力。

［1］ 胡 鹏.基于接驳的慢行交通一体化研究［D］.武汉:华中科技大学，2008.

［2］ 黄文娟.轨道交通与常规公交换乘协调研究［D］.西安:长安大学，2004.

［3］ 谢立宏.城市轨道交通与快速公交换乘时间衔接分析［J］.城市轨道交通研究，2010(6):59-62.

［4］ 覃 煜，晏克非.轨道交通枢纽换乘效率DEA非均一评价模型［J］.长安大学学报(自然科学版)，2002，22(4):48-54.

［5］ 韩宝明，李得伟.铁路客运专线换乘枢纽交通设计理论与方法［M］.北京:北京交通大学出版社，2010:75-76.

［6］ 毛宝华，刘明君.轨道交通网络化运营组织理论与关键技术［M］.北京:科学出版社，2011:122-123.

［7］ 周雪梅，杨晓光.基于ITS的公共交通换乘等待时间最短调度问题研究［J］.中国公路学报，2004(2):82-84.

［8］ 余红红，柳 波.慢行交通衔接常规公交的换乘时间分析［J］.公路与汽运，2012(4):50-52.

［9］ 王秋平，李 峰.城市其他客运交通换乘轨道交通协调探讨［J］.西安建筑科技大学学报(自然科学版)，2003，35(2):136-139.