求解绝对值方程的光滑牛顿算法
张焱娇
(天津大学,天津300072)
绝对值方程一般数学表达式如下:

其中:|x|表示的是对x的每个分量取绝对值.本文中研究的矩阵A和B矩阵为方阵:
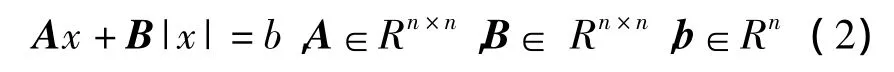
绝对值方程是Rohn在中首次出提出的.目前求解绝对值方程的算法针对B=-I,
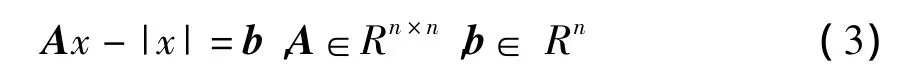
[1-5]中讨论了绝对值方程(1)(2)和(3)的一些性质.下面简单列举一下这些性质:如果绝对值等式(1)、(2)、(3)是可解的,则绝对值方程或者有惟一解,或者有多重解[3],一般的绝对值规划(1)可以转换成一个线性互补问题[4].
Mangasarian提出算法是:将绝对值等式(3)转化成分段线性的凹极小化问题,利用连续化线性算法来求解.之后在参考文献[6]又中提出了一种广义牛顿法来求解绝对值方程(3),要求A的奇异值严格大于1,此方法的有线性收敛性质已经得到了证明.之后Oleg Prokopyev在参考文献[7]中将绝对值方程(3)问题转化为0-1混合线性规划来进行求解.本文所做的工作是利用光滑牛顿算法来求解问题(2)和(3),光滑化的思想[8-9].
本文中证明了在矩阵A的主对角线上的元素的绝对值大于矩阵B的主对角元素的绝对值,矩阵A、B对于可交换条件下,算法是适定的,具有全局收敛性质.根据参考文献[10-11],绝对值方程的可解性问题是一个NP难的问题,所以本文不讨论绝对值方程解的存在性.
现将本文所使用的符号如下:对于向量x∈Rn,若x>0表示的是向量x的每个分量都大于0;‖x‖表示向量x的欧式范数,对于向量y,s∈ Rn对于函数F:Rn→Rm,F'(x)表示函数F在点的Jacobi矩阵.
1 算法设计
1.1 NCP 函数
定义 设函数φ(a,b):R×R→R,如果满足φ(a,b)=0⇔a≥0,b≥0,且 ab=0 性质.
1.2 光滑牛顿法
定理1 对于绝对值等式Ax+B|x|=b,其中x∈Rn,A∈Rn×n,B∈Rn×n若矩阵(- A+B)和矩阵B可逆,矩阵A和矩阵B对于乘法可交换时,则该问题可等价转换为如下:
(-A+B)s-(-A-B)y=2Bb y≥0,s≥0,yTs=0
证明:见参考文献[5]
推论1 当B=-I时,求Ax-|x|=b解的解,若矩(A+I)阵可逆,那么(2)等价转化为求解如下的问题:

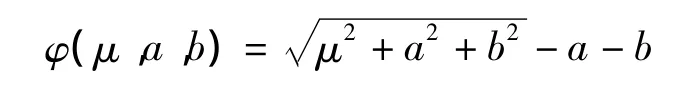
现在在利用光滑后的F-B函数,来构造向量值函数:
Ψ(μ,y,s)=(φ(μ,y1,s1),φ(μ,y2,s2),…,φ(μ,yn,sn))T

定义的光滑化函数H:R2n+1→R(2n+1),如下:其中 z=(μ,y,s),显然‖H(z)‖ =0当且仅当 μ=0,且(y,s)是线性互补问题(4)的解.只要求出z*使得‖H(z*)‖=0,就可以求出绝对值方程(2)的解.对于任意(μ,y,s)∈R++× Rn× Rn,函数 H(z)一定是连续可微的.且函数H(z)Jacobi矩阵为:

下面对一些符号予以说明:

算法1(求解形如(2)的绝对值等式的光滑牛顿法)
步骤0选择适当的 δ,σ∈(0,1),μ0>0 和(y0,s0)∈R2n是初始向量.令 z0:=(μ0,y0,s0),选择适当的β>1使得‖H(z0)‖≤βμ0,令 e0=(1,0,…,0)T,令 k:=0;
步骤1如果‖H(zk)‖=0,停止,zk则是我们所求的最优解;否则,跳至步骤2;
步骤2 计算 Δzk:=(Δμ0,Δy0,Δs0)∈R ×Rn×Rn,其中Δzk满足以下的牛顿方程:
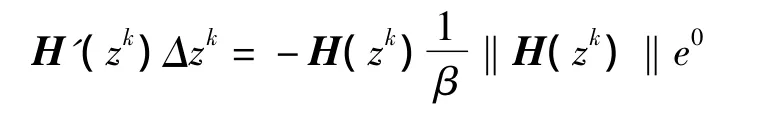
根据(5)的具体形式,可以得到:

步骤3令λk是1,δ,δ2中使下式成立的最大值.
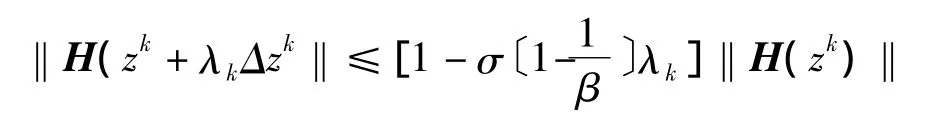
步骤4 令 zk+1:zk+λkΔzk取 k:=k+1,调到步骤1.
步骤5求解方程y-s=2Bx
1.3 算法的性质
在参考文献[8]中,有如下结论成立:
命题1 设{zk=(μk,yk,sk)是由算法 1 产生的迭代序列,则有以下的结论成立:
迭代过程中,对任意迭代点都有μk>0;序列{‖H(zk)‖}是单调下降序列;算法迭代的过程中序列{μk}是单调下降的;设β>1是算法中给定的常数,定义集合:N(β):={z∈R+×Rn×Rn:‖H(z)‖≤βμ}则我们在迭代过程中,对于任意的k∈{1,2,…,n},zk∈N(β);
定理2若果矩阵(A+B),(-A+B)和矩阵B可逆,矩阵A和B矩阵对于乘法可交换,并且矩阵A的主对角线上的元素的绝对值严格大于矩阵B的主对角线上元素的绝对值,则算法1中的步骤2的牛顿方程一定是可解的,说明此算法一定是适定的.
证明:先介绍一些证明中涉及的符号:
cii:=min{- aii- bii,aii+bii},
c=(c11,c22,cnn)C:=diag(c)
dii:=max{- aii- bii,aii+bii},
d=(d11,d22,knn)D:=diag(d),i∈{1,2,…,n}
由假设矩阵A的对角线上的元素的绝对值大于对应B的位置元素的绝对值,并且下式成立:
|aii-1|bii<1,i∈{1,2,…,n}
由参考文献[13],推论 3.2区间[C,D]是正则的.即任意的,m,n∈[0,1],mC+nD 是可逆的.

Ψs(A+B)-Ψy(-A+B)是可逆的
⇔Ψs(A+B)-Ψy(A+B)-1(A+B)(-A+B)是可逆的
⇔Ψs(A+B)-Ψy(A+B)-1(A+B)(-A+B)是可逆的,因为AB=BA
⇔Ψs-Ψy(A+B)-1(-A+B)是可逆的,因为矩阵是(A+B)可逆的.
那么算法1的步骤2的牛顿方程也一定有解的.
推论2当矩阵B=-I时,绝对值方程(3)有以下的结论成立:如果矩阵(I-A)可逆,并且矩阵的主对角线上的元素同时大于1或者小于-1,则算法中的牛顿方程是可解的.
2 算法的性质
本节证明在矩阵AB满足适当关系的条件下,算法1有全局收敛性.
定理3矩阵(I-A),(I+A)是可逆的,并且矩阵A的主对角线上的元素同时严格大于1或者严格小于-1时,则通过算法1产生的{zk:=(μk,yk,sk)}是有界序列.
证明 由命题1的结论可知序列{μk}是单调下降有下界的序列{zk}:={μk,wk},为了说明序列的有界性{wk},只需在说明序列是有界序列即可,其中{wk=(yk,sk)}.利用反证法证明序列{wk}是是有界序列{wk},假设序列无界,则可知其部分序列{yk},{sk}至少有一个是无界序列.则无界序列,必须满足以下三种情况之一:1)序列{yk}无界,序列{sk}有界;2)序列{yk}有界,序列{sk}无界;3)序列{yk},{sk}无界;
1)序列{yk}无界,序列{sk}有界的
因为序列{yk}无界,则存在指标 i0∈{1,2,…,n},使得|(yk)|→∞,当 k→∞时,
|((I+A)sk+(I-A)yk+2b)i0|→∞,k→∞,
此时就一定会出现‖H(zk)‖→∞,当k→∞,这与命题2.1中序列‖H(zk)‖是单调下降有界的序列产生矛盾.所以情况(1)是不可能出现的.
2)序列{yk}有界,序列{sk}无界的(同(1))
3)序列{yk},{sk}同时是无界的
若实数对{i0,j0}其中 i0∈{1,2,…,n},j0∈{1,2,…,n}且满足i0≠j0则此时可以归结为上述的(a)、(b)两种情况之一,会出现矛盾,无界序列无法产生.下面讨论另外一种情况:即为对于任意t0∈{1,2,…n},只要|(yk)t0|→∞ 则必有|(sk)t0|→∞并且其逆命题也成立.下面在进一步讨论,当k→∞时:
若(yk)t0→ +∞,(sk)t0→ +∞ 时,((I+A)sk+(I-A)yk+2b)t0→+∞,
若(yk)t0→ +∞,(sk)t0→ +∞ 时,((I+A)sk+(I-A)yk+2b)t0→+∞
若(yk)t0→+∞,(sk)t0→-∞时,有
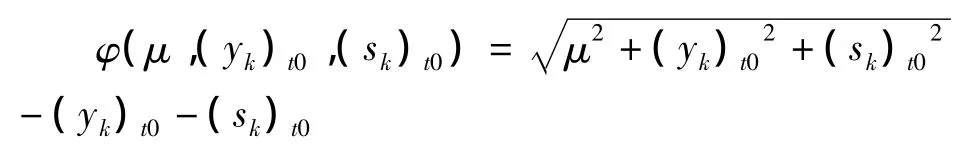
显然当 k→∞,有|φ(μ,(yk)t0,(sk)t0|→∞,则此时同样可以的得到函数H(zk)的范数‖H(zk)‖→∞,与算法性质矛盾.综上所述,假序列{zk:=μk,yk,sk)}也有界的.
定理4 假定矩阵(I-A),(I+A)是可逆的,矩阵A的对角线上的元素同时大于1或者同时小于-1,则产生的序列{zk}有以下性质
证明方法类似于参考文献[13]
3 数值计算结果与结论
数值实验所用电脑规格为:CPU是2.93 GHz,内存2.00 GHz.数值实验的具体绝对值方程产生过程如下:产生一个矩阵保证其每一个对角元素都同时大于1或者同时小于-1;随机选取向量x∈Rn,其中的每个分量符合[-10,10]的均匀分布;计算出b=Ax-|x|.
本文将对n等于500、800、1000的情况分别进行数值实验,每组实验中,连续随机产生50个绝对值方程.在数值实验的程序中‖Ax-|x|-b‖<10-6作为算法的终止条件;循环的最高次数定为40次;当算法终止是若‖Ax- |x|-b‖ <10-6,则认为失败.
相关参数值为 σ =0.8,σ =0.0001,μ0=0.0001;x0为随机产生的维向量x0i,其分量符合[-10,10]之间的均匀分布.

表1 数值结果(矩阵的主对角线上的元素严格大于1或者严格小于-1)
4 结语
本文提出的光滑化牛顿算法,分别对形如Ax+B|x|=b和Ax-|x|=b的绝对值方程组进行求解,并且证明了在一定的条件下此算法是全局收敛的.在此之前,要求的是在区间[I-A,I+A]是正则的,对矩阵A的奇异值等性质要求较高.
在理论证明中,条件“当矩阵(B+A)和矩阵(B-A)可逆,矩阵AB对乘法满足交换律,以及矩阵A的主对角线上的元素的绝对值大于矩阵B主对角线上的绝对值时,证明了算法是适定的,并且当矩B=-I阵时,更证明了该算法的全局收敛性,”在未来的研究中,可以尝试证明矩阵B的一般情形是算法的全局收敛性.
参考文献:
[1]MANGASARIAN O L.Knapsack feasibility as an absolute value equation solvable by successive linear programming[J].Optimization Letters,2009,3(2):161 -170.
[2]OLEG P.On equivalent reformulations for absolute value equations[J].Computational Optimization and Applications,2009,44(3):363-372.
[3]FUKUSHIMA M.The primal Douglas-Rachford splitting algorithm for a class of monotone mappings with application to the traffic equilibrium problem [J].Mathematical Programming,1996,72(1):1-15.
[4]NAGURNEY A,DONG J,ZHANG D.A supply chain network equilibrium model[J].Transportation Research,2002,Part E 38(5):281-303
[5]PANG TRINKLE J C.Complementarity formulations and existence of solutions of multi-rigid-body contact problems with Coulomb friction[J].Mathematical Programming,1996,73(2):199-226.
[6]CHEN CH,MANGASARIAN O L.Smoothing methods for convex inequalities and linear complementarity problems[J].Mathematical Programming,1995,71:51-69.
[7]MANGASARIAN O L,MEYER R.Absolute Value Equations[J].Linear Algebra and Its Applications,2006,419:359 -367.
[8]CHEN C, MANGASARIAN O L.A class of smoothing functions for nonlinear and mixed complementarity problems[J].Computational Optimization and Applications,1996,5:97-138.
[9]QI L Q,SUN D,Smoothing functions and smoothing Newton method for complementarity and variational inequality problems[J].Jouranal of Optimization Theory and Applications,2002,113 -121.
[10]ROHN J.A theorem of the alternatives for the equation Ax+B|x|=b[J].Linear Multilinear Algebra,2004,52(6):421-426.
[11]MANGASARIAN O L .Absolute value programming[J].Computational Optimization and Applications,2007,36:43 -53.
[12]MANGASARIAN O L.Absolute value equation solution via concave minimization[J].Optimization Letters,2007,1(1):3-8.
[13]高竹峰.求解绝对值方程组的牛顿算法[D].天津:天津大学,2009.

