在线精密单点定位服务系统在山区像控测量中的可行性分析

巩英明,王俊强,张 飞

(1.68029部队,甘肃 兰州 730020;2.96633部队,北京 102218)

0 引 言

在大比例尺地形图航空摄影测量任务中,航测所需像控点的测量主要依靠GPS载波相位实时动态(RTK)、GPS静态相对测量或全站仪测量等方式,这些方式都能获得满足测量精度的数据。在山地困难地区,尤其是西部地区,呈现大地控制点少、地形起伏较大等特点,使得在这些测区野外实施像控点测量时,利用RTK或者GPS静态相对测量方式的可行性不高。随着精密单点定位技术的不断成熟,目前精密单点定位技术能够实现非差分条件下达到厘米级别的单点定位精度[1],将精密单点定位技术应用于山区像控点测量中,能够克服传统GPS静态相对测量方式对已知大地控制点的依赖,以及RTK差分信号传输受地形起伏影响大的缺点,适应于高山地区像控野外测量任务。本文以某西部高山地区大比例尺地形图航空摄影测量实例为基础,对几种在线精密单点定位服务系统应用于像控测量的可行性进行了分析。

1 精密单点定位技术原理

精密单点定位技术(PPP)是由美国喷气推进实验室(JPL)的Zumberge于1997年提出的。20世纪90年代末,由于GPS全球跟踪站的数量急剧上升,全球GPS数据处理工作量不断增加,计算时间呈指数上升。为了解决这个问题,作为国际GPS服务组织(IGS)的一个数据分析中心,JPL提出了这一方法,用于非核心GPS站的数据处理[2]。

该技术具体实现是利用IGS提供的高精度的GPS精密卫星星历和卫星钟差,以及单台双频GPS接收机采集的载波相位观测值,采用载波相位与伪距组合观测方程进行精密单点定位,传统模型为[3]

dtrop+λN+δmIF+ε(φIF),

dtrop+dmIF+ε(PIF)，

(1)

式中:φIF,PIF分别表示载波相位和伪距的无电离层组合观测值;dtr表示接收机钟差;dts表示卫星钟差;dtrop表示对流层延迟;δmIF和dmIF表示包括相对论效应、固体潮、硬件延迟等一系误差改正;λ和N分别为组合后的载波波长和组合模糊度;ε(φIF)和ε(PIF)为观测值噪声误差。在多历元观测下,可根据上述模型采用序贯最小二乘法或卡尔曼滤波法解算。

精密单点定位的优点在于进行精密单点定位时,除能解算出测站坐标,同时还能解算出接收机钟差、卫星钟差、电离层和对流层延迟改正信息等参数,这些结果可以满足不同层次用户的需要(如研究授时、电离层、接收机钟差、卫星钟差及地球自转等)。

2 几种在线精密单点服务系统

随着PPP技术和网络技术的不断发展,国内外有不少科研机构相继推出了在线网络定位服务,这些服务绝大部分面向全球用户免费开放[4]。

2.1 PPP在线定位服务流程

在线精密单点服务系统是将精密单点定位技术与网络技术相结合,可全天候自动为用户提供高精度的精密单点定位解算。服务流程如图1所示,用户只需登入相应服务网站,将观测数据上传服务器,系统将自动下载相应的精密星历,并基于精密单点定位技术自动解算,最后将最终解算的成果通过邮件发送给用户。

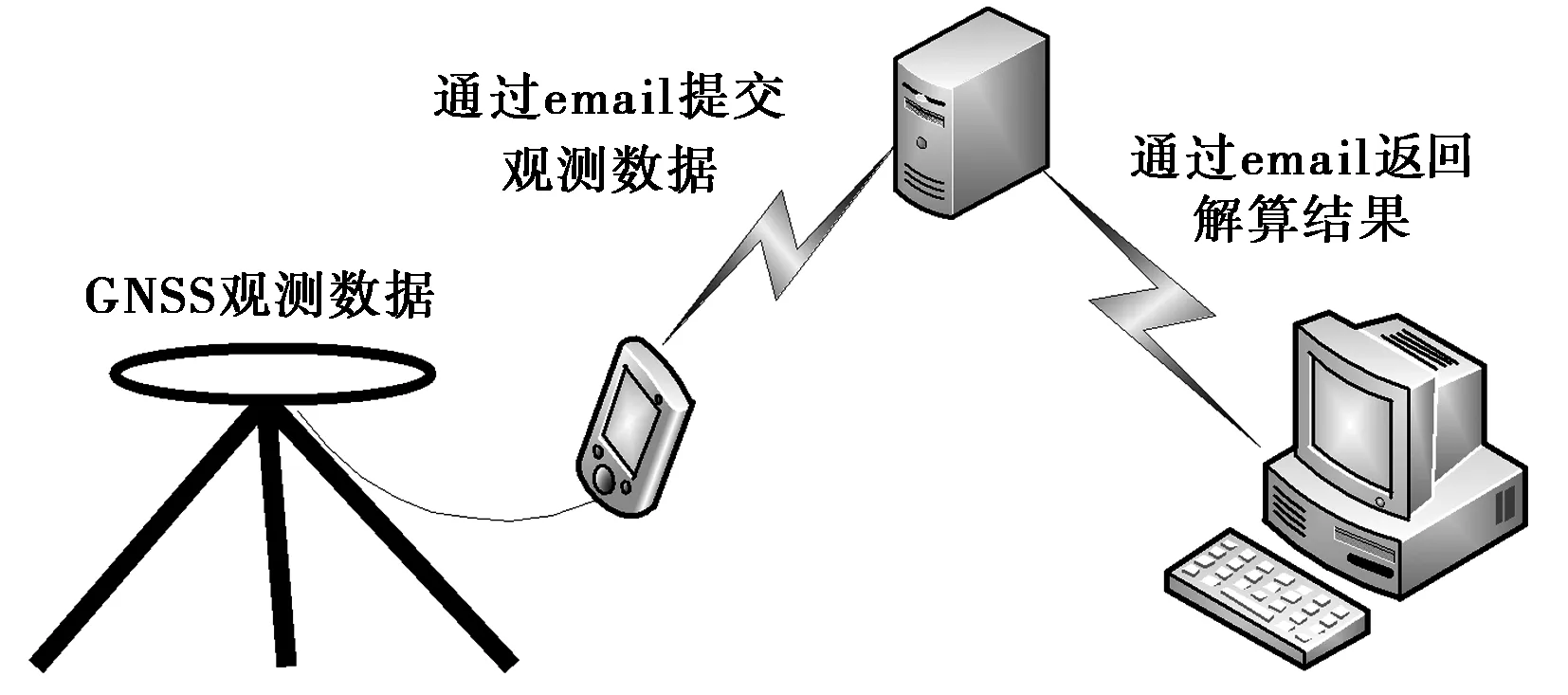
图1 在线精密单点定位数据处理流程

2.2 几种在线精密单点服务系统概述

目前全球主要有四大在线PPP服务系统,分别是加拿大自然资源颁布的CSRS-PPP[5]、新伯伦瑞克大学颁布的GAPS-PPP[6]、美国气动力实验室(JPL)颁布的APPS[7]以及西班牙GMV公司的magicGNSS[8].

通过对这四种服务系统在GPS观测数据处理中的反复试用可得如表1所示数据处理情况。从表中可知四种服务系统均能处理静态GPS观测数据,并且均能够获得ITRF框架下坐标数据,其中CSRS-PPP处理效率最高,表1示出了各服务系统的对比情况。

精密单点定位中影响数据解算收敛时间的因素很多,如观测数据质量、采样间隔、误差估计模型、卫星空间几何构型以及用户所要求达到的精度等[9]。为了获取在线精密单点定位服务系统解算的收敛时间,取某观测数据质量良好的静态点位数据,采样间隔为15 s,利用CSRS-PPP系统解算可知,三方向坐标值在10 min左右时间收敛,如图2所示。因此,在实际静态单点测量像控点时采集半小时即满足要求。

表1 各在线精密单点服务系统对比情况

图2 点位解算收敛时间

3 算例分析

为了检验上述几种在线精密单点定位服务系统解算数据的稳定性和精度,选取某待建高速公路航摄带状区域内基础控制网部分数据进行验证,控制网点位成果已通过高精度数据后处理软件GAMIT解算获取,精度满足C级控制点要求。各在线精密单点定位服务系统解算成果与后处理软件GAMIT解算的成果进行对比,以分析获取结论。点位分布情况如图3所示,其中D字母开头点位为首级控制点,静态数据测量时间为90 min,X字母开头为加密点,静态测量时间为60 min.

3.1 各精密单点定位服务系统处理数据稳定性比较

图3 点位分布情况

图5 各系统解算与真值的比较情况

3.2 各精密单点定位服务系统解算精度比较

将各精密单点定位服务系统解算成果与经高精度数据后处理软件GAMIT解算后结果(视为“真值”)对比可分析各系统的解算精度。图5示出了各系统解算与真值的比较情况,从图中可知,CSRS-PPP的解算精度最优。同理,可利用外符合精度计算公式进一步分析各定位服务系统的精度。经计算可得:CSRS-PPP三个方向(N,E,H)外符合精度分别为±7.2 cm、±4.0 cm、±5.1 cm;magicGNSS解算三方向外符合精度分别为±7.7 cm、±8.7 cm、±8.0 cm;APPS解算三个方向外符合精度分别为±8.7 cm、±10.5 cm、±10.7 cm;GAPS-PPP解算三个方向外符合精度分别为±6.8 cm、±10.0 cm、±7.8 cm.以上可知,系统解算的精度由高至低依次为CSRS-PPP、magicGNSS、GAPS-PPP、APPS,四种在线定位服务系统外符合精度均满足大比例尺地形图航摄像控点测绘精度的要求[10],可应用于山地像控点测绘中。

综合以上分析,从数据解算量、数据解算时间以及解算的稳定性和精度等方面考虑,CSRS-PPP系统要优于其他系统。因此,在实际运用中,CSRS-PPP系统为数据解算的最佳选择。由于利用精密单点定位解算后数据精度的检核条件不够,因此在实际作业过程中,可利用CSRS-PPP系统解算为主,其他系统解算作为验证,通过比对的方式,筛选出可靠的结果。在线精密单点定位服务系统获取的是ITRF框架下的坐标,根据实际坐标结果需求,可利用测区七参数转换模型将其转换成指定坐标系,利用高精度区域似大地水准面模型可转换大地高为正常高。

4 结束语

本文通过实际算例分析了四种在线精密单点定位服务系统的数据解算稳定性和精度等情况,结果表明,四种在线精密单点定位系统均可应用于山地像控点测量,实际作业中可根据对数据处理需求的情况,采用不同的系统进行解算,为控制点稀少的山地测区像控点测量提供了快速便捷的解决方法。

[1] 王玉龙,李秀丽，王建忠，等.精密单点定位技术在测绘生产中的应用[J].地矿测绘,2012,28(2):23-25.

[2] 刘焱雄,周兴华,张卫红，等.GPS精密单点定位精度分析[J].海洋测绘,2005,25(1):44-46.

[3] 刘经南,叶世榕.GPS非差相位精密单点定位技术探讨[J].武汉大学学报·信息科学版,2002,3(27):234-239.

[4] 高 攀,郭 斐,吕翠仙，等.精密单点定位在线GNSS数据处理精度比较分析[J].全球定位系统,2011,36(3):21-23.

[5] NATURAL RESOURCES CANADA. Online database(CSRS On-line Database)[EB/OL]. [2014-04-05].http://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php.

[6] UNIVERSITY of NEW BRUNSWICK. Online GAPS[EB/OL]. [2014-04-05]. http://gaps.gge.unb.ca.

[7] JET PROPULSION LABORATORY. Automatic precise positioning service-APPS[EB/OL]. [2014-04-05].http://apps.gdgps.net.

[8] GMV.magicGNSS [EB/OL]. [2014-04-05].http://magicgnss.gmv.com/ppp.

[9] 郑作亚,党亚民,卢秀山,等. GPS精密单点定位中影响收敛时间的因素及措施分析[J].大地测量与地球动力学,2009,29(5):108-111.

[10]国家测绘局测绘标准化研究所.GB/T 7931-2008 1:500、1:1000、1:2000地形图航空摄影测量外业规范[S].北京:中国标准出版社,2008.