基于大数分解的门限秘密共享方案
李滨
(成都师范学院数学系,四川 成都611130)
0 引言
现代密码体制的设计思想是使体制的安全性取决于密钥,密钥管理便成为网络环境下信息安全的关键内容,密钥管理者尤其需要对主密钥加强管理.但在现实的使用中却存在几种不确定的情况:第一种是出现管理者自己不经意泄露主密钥的情形,第二种是出现主密钥被他人窃取的情形,第三种是出现管理者丢失了主密钥的情形,第四种是出现主密钥被他人恶意毁坏的情形.无论出现哪种情况都会导致整个系统处于不安全的状态,系统中的信息要么受到攻击,要么再也不能使用了.后来人们采取给可信的用户发放密钥副本的方式来解决这个问题,但这些用户又有多大的信用度呢?在出现背叛行为时系统同样处于不安全的状态.目前真正能够解决这个问题的唯一办法就是在密钥管理中引入秘密共享的思想.所谓秘密共享,是指在多个参与者之间共享主密钥k的思想,设参与者集合为P={P1,P2,…,Pn},则根据一定的共享方案可计算出每个参与者得到的信息,记作{k1,k2,…,kn},其中ki由参与方Pi秘密保存,称为一个子密钥,只有参与者集合P的某些特定的子集集合Ⅰ才能利用其各自掌握的子密钥一起重构主秘密,这些子集构成的集合也被称为访问结构.
秘密共享是密钥管理的一种核心技术,和其他密码技术一样,它源自现实世界,是现实世界在数字领域的映像.以银行为例,银行的保险库是银行的核心重地,由谁来单独掌管都是不合适的,所以,一般都是交给几个人来共同掌管.例如,有5个出纳,规定需要3个出纳在一起才能打开保险库.这一措施有两个优点:一是杜绝了不足3个人开库作案的隐患;二是5个人一共有10种开库的方法,防止了一个人遗忘密钥或缺席而打不开保险库的可能.这一设想实现了3个人共享一个秘密的思想,密码学把这种秘密共享方案称为(3,5)门限方案.一般来说,(t,n)门限方案是一类特殊的秘密共享方案.Shamir[1]和Blakley[2]于1979年先后各自独立地提出了门限方案的思想,并分别采用代数法和几何法将其实现.在(t,n)门限方案中,n表示参与者个数,t表示为了重构秘密需要的最少子密钥数,其访问结构是所有t元素子集构成的集合.门限方案是理想的秘密共享方案.它的基本做法就是将一个主密钥k拆成有限个子密钥k1,k2,…,kn,这些子密钥满足由其中的t(1<t<n)个ki(1≤i≤n)可推出主密钥的重构性要求和少于t个的ki不能推出k的安全性要求,只有具备重构性和安全性的秘密共享才是完备的秘密共享.接下来掌管主密钥的庄家将这n个子密钥k1,k2,…,kn分发给n个参与者,由于重构密钥至少需要t个子密钥,所以暴露u(u≤t-1)个子密钥不会危及主密钥,从而少于t个参与者的共谋不能得到主密钥;同时,如果一个子密钥被丢失或毁坏仍可恢复主密钥.
(t,n)门限方案可以利用不同领域的数学知识来构造,目前比较著名的有基于有限域上的拉格朗日插值多项式的Shamir方案和利用有限域上的超平面构造的Blakley方案,还有基于Reed Solomon(RS)码的McEliece方案[3],基于中国剩余定理的Asmuth Bloom方案[4],以及基于有限域上的矩阵运算的Karnin-Greene-Hellman方案[5]等.针对不同的应用需求,人们对上述的各种门限方案进行改进,提出了多种门限方案的变体[6-10].总之从数学的不同领域只要满足其中一个目标可由某个集合中的t个结果所确定,但任何一个附加结果都是多余的情况,都可以用来构造门限方案.本文中正是通过幂乘的指数结构形式,利用大数分解的困难性和不定方程整数解的存在性来构造了一个(t,n)门限方案.
1 基于大数分解的(t,n)门限方案设计
在密码学中,基于大整数分解的公开密钥密码体制的安全性依赖于大整数分解问题,大整数分解问题是一个数学难题,它可以被描述为:给定两个大素数p,q计算乘积pq=N很容易;反之,给定整数N,求N的素因数p,q使得N=pq是一个计算上困难的问题.
对于一个多元一次不定方程a1x1+a2x2+…+amxm=M,其中a1,a2,…,am,M 都是整数,m≥2,并且a1,a2,…,am都大于零.当 M 充分大时,此方程有正整数解的充要条件是gcd(a1,a2,…,am)|M.
我们具体来看一下基于大数分解的(t,n)门限方案的实现.设
基于大数分解(t,n)门限方案中的n个参与者为P1,P2,…Pn.庄家 D∉{P1,P2,…,Pn}.D 想让P1,P2,…,Pn分享主密钥k,D秘密地分配给他们每人一个关于主密钥k的子密钥.当P1,P2,…,Pn中的任意t个人给出他们的子密钥后可以重建主密钥k,而任意t-1个参与者给出他们的份额后不能重建主密钥k.
基于大数分解的(t,n)门限方案可以描述如下:
1)庄家D 取两个大素数p 和q,计算N=pq,φ(N)=(p-1)(q-1),并将N 公开,p,q,φ(N)保密.
2)庄家D选取两两互素的大整数序列e1,e2,…,en对于主密钥k<N,使得kei>N(其中1≤i≤n),对1≤i≤n计算主密钥幂ri=keimodN,D将ri秘密地分配给参与者Pi,1≤i≤n.
3)对1≤i≤n,令集合Ai={dσ(i)|σ(i)表示下标j1j2j3…jt,其中j1=i,j2j3…jt是1到n中除去i的n-1个数中选取t-1个数的自然递增排序},显然,Ai中共有个元素.
例如:当n=5,t=3时

庄家D秘密地随机选取正整数δ,从序列ei(1≤i≤n)中任取t个数ei1,ei2,…,eit,组建下列结构方程并计算dσ(i),

由于gcd(e1,e2,…,en)=1,因此不定方程(*)有一个正整数特解{dσ(i1),dσ(i2),…,dσ(it)},能构成(*)的方程共有Ctn个,这样的正整数解共有Ctn组,每一个方程的特解称为一个同组组合.可以从所有的同组组合中各自找到Ai的一个元素.例如:当n=5,t=3时,A2中的元素d215可以从同组组合{d125,d215,d512}中找到,而这一个同组组合是不定方程e1d125+e2d215+e5d512=1+δφ(N)的一个特解.接下来庄家D将集合Ai秘密地分配给参与者Pi,1≤i≤n.假设n个参与者中的任意t个成员Pi1,Pi2,…,Pit要计算主密钥k,他们分别拿出自己的ri1,ri2,…,rit和Ai1,Ai2,…Ait中对应选出的同组组合{dσ(i1),dσ(i2),…,dσ(it)}.
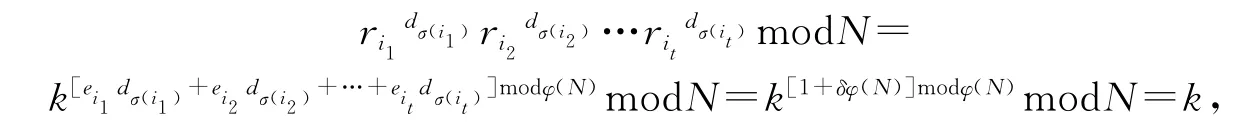
从2)、3)步可以看出子密钥的构成是ki={ri|Ai的元素},其中i=1,2,…,n.值得注意的是必须要求kei>N,否则,ri=keimodN=kei就是普通的指数,系统就会不安全.另一方面,庄家对两个大素数p和q以及欧拉函数φ(N)必须保密,否则,攻击者可以从结构方程(*)解出一个正整数特解{dσ(i1),dσ(i2),…,dσ(it)},从而得出主密钥.由于N公开,想要计算p和q是非常困难的,因此,该门限方案的安全性也依赖于大数分解的困难性.显然,从主密钥k的计算式来看,该方案需要t个参与者才能恢复主密钥,多于t个参与者时,从中任选t个参与者也能恢复主密钥,但低于t个参与者合谋却因为k的计算式中缺少足够的乘积项而不能计算出主密钥,甚至得不到主密钥k的任何信息,所以该门限方案是无条件安全的.综上所述,该门限方案满足秘密共享的重构性和安全性要求,是一个完备的秘密共享方案.
下面我们举例来看看这个(t,n)门限方案的实现方式.
例:庄家D选定t=3,n=5,k=13,p=7,q=11,δ=2,

计算N=77φ(N)=60,将N 公开.
计算r1=ke1modN=137mod77=62,r2=ke2modN=135mod77=76,
r3=ke3modN=132mod77=15,r4=ke4modN=1311mod77=13,r5=ke5modN=133mod77=41.
取d123=8,d213=9,d312=10为一个同组组合.
取d124=5,d214=15,d412=1为一个同组组合.
取d125=9,d215=5,d512=11为一个同组组合.
取d134=7,d314=14,d413=4为一个同组组合.
取d135=9,d315=14,d513=10为一个同组组合.
取d145=2,d415=7,d514=10为一个同组组合.
取d234=7,d324=10,d423=6为一个同组组合.
取d235=13,d325=13,d523=10为一个同组组合.
取d245=8,d425=3,d524=16为一个同组组合.
取d345=12,d435=8,d534=3为一个同组组合.
从上述同组组合中求出集合Ai,1≤i≤5.

这样得到5个子密钥:

庄家将ki秘密地分配给Pi,1≤i≤5.
假若P3,P4,P53个参与者在一起只要通过下面计算就可以恢复主密钥k.

这里需要说明的是在该门限秘密共享方案的实际应用中一般要求大素数p和q都要是12位以上的数.但上面这个例子我们只需要呈现本方案是怎样实现的,为了便于计算,把其中的p和q取成了两个小素数.
2 结束语
随着人们对信息安全研究的逐渐深入,秘密共享已成为密码学中的一个重要分支,它的理论日臻完善,应用范围也从起初的密钥管理扩展到了数字签名、电子选举、电子拍卖、纠错码等诸多方面.利用数学领域各研究方向的成熟知识设计新的秘密共享方案是目前国际密码界的研究趋势.对于一个大的正整数N,如何判断N是否为素数和如何把N 分解成素数之积,是一个计算上困难的问题.人们对这两个问题已经研究了上千年,而且算法在不断地改进,对于素数的判断问题是相对容易的.但对于大数分解问题,1988年用400台计算机联网运行326天,对100位十进制数分解成功.最新的记录已提到129位十进制数.至今还不存在对一个大整数分解的一般性的有效解决算法.目前最好的分解算法是数域筛选法,按照它的渐近时间估计值,对于一个200位十进制数,即使以每秒107次运算的超高速电子计算机进行因子分解,也要花费108年.著名的RSA公钥密码体制是1978年由Rivest、Shamir和Adleman提出,并以它的3个发明者的名字命名的,它的安全性依赖于大数的因数分解的困难性.本文中提出的(t,n)门限秘密共享方案的安全性,同样依赖于大因数分解的困难性,但针对的内容不同,结构不同,作用不同.该方案设计的思路和方法是一种创新,结果显示该门限方案是一种安全完备并且易于实现的秘密共享方案.
致谢 作者衷心感谢审稿人对本文所提出的十分宝贵的修改意见和给予的帮助.
[1]Shamir A.How to share a secret[J].Communications of the ACM,1979,22(11):612-613.
[2]Blakley G R.Safeguarding cryptographic keys[C]//AFIPS Conference Proceedings.New Jersy:AFIPS Press,1979:313-317.
[3]McEliece R J,Sarwate D V.On sharing secrets and Reed-Solomon codes[J].Communications of the ACM,1981,24(3):583-584.
[4]Asmuth C,Bloom J.A modular approach to key safeguarding[J].IEEE Transactions on Information Theory,1983,29(2):208-210.
[5]Karnin E D,Green J W,Hellman M E.On sharing secret systems[J].IEEE Transactions on Information Theory,1983,29(1):35-41.
[6]Xiao L,Liu M.Threshold schemes with weights[J].Journal of Systems Science and Complexity,2004,17(4):578-581.
[7]Li B.Difference secret sharing scheme based on special access right[J].Journal of Sichuan University(NSE),2006,43(1):78-83.
[8]Dehkordi M H,Mashhadi S.New efficient and practical verifiable multi-secret sharing schemes[J].Information Science,2008,9(178):2262-2274.
[9]Nojoumian M,Stinson D H,Grainger M.Unconditionally secure social secret sharing scheme[J].IET Information Security,2010,4(2):202-211.
[10]Nojoumian M,Stinson D R.On dealer-free dynamic threshold schemes[J].Advances in Mathematics of Communications,2013,7(1):39-56.

