180°弯曲水槽内床面冲淤演化过程数值模拟
, ,
(1.天津大学 仁爱学院建筑工程系,天津 301636;
2.大连理工大学 水利工程学院,大连 116024;
3.长江科学院 水力学研究所,武汉 430010)
1 研究背景
河道内的水流和泥沙输运以及河床冲淤变化是水利工程中主要的研究对象,而蜿蜒曲折又是天然河道最为常见的河流形态,弯曲河道内的水流由于受离心力和水面横比降造成的压力梯度共同作用的影响,形成弯曲河道典型的二次流(横向环流)特征,其与主流向流动的结合形成复杂的三维螺旋流动,具有显著的三维特性[1-4]。
由于二次流在河道断面上表现出表层向凹岸流动,底层流向凸岸的环流特性,从而造成近河床处泥沙不断从凹岸向凸岸输移,加之河床冲淤过程中的横向底坡使输沙方向偏离水流方向,并且随着横向底坡的越来越大,这种影响愈发明显,尤其对于二次流强度显著和横向坡度较大的强弯曲河道[5],以往二维数值模拟中半经验性的二次流校正[6]和考虑横向底坡造成输沙偏离流动方向的模型[6-8]难以适用这些问题,为此本文采用Engelund[9-10]横向输沙模型,并考虑河床变形所引起的临界起动切应力变化[11],采用流动和地形冲淤相同时间步的方法模拟180°弯曲水槽内床面非恒定的地形冲淤演化过程。
2 数值模型
2.1 水动力模型
关于水动力过程的求解,本文基于变量交错定义的三角形网格,采用有限体积分层积分方法对RANS方程进行离散[12],标准k-ε紊流模型和显式2步投影方法求解RANS方程。首先求解包含对流项和扩散项的动量方程,得到中间时刻的速度场;其次求解由离散连续性方程和动量方程得到的关于压力的Poisson方程,得到压力校正项;最后将其带入动量方程对中间时刻速度场进行修正,从而得到新时刻的速度场和水位[8]。
2.2 泥沙输运模型
计算地形演化过程的泥沙连续性方程可以表示为
(1)
式中:p′表示孔隙率;qsx和qbx分别表示x方向上的悬移质和推移质输沙率;qsy和qby分别表示y方向上的悬移质和推移质输沙率。
选用Van Rijn推移质输沙率公式[13]计算推移质输沙率
图4显示非恒定的地形冲淤演变过程,分别显示50,100,200,480 min 4个时刻的地形冲淤厚度等值线。从图4中可以看出弯曲水槽的冲淤变化基本都发生在弯段内,沿弯段凸岸一侧发生淤积,凹岸侧发生冲刷。随着水流的不断作用,凸岸侧不论是淤积量还是淤积范围都在增长,相应地凹岸一侧的冲刷深度和冲刷范围也在不断增加,受弯道二次流横向输沙的影响,凹岸一侧泥沙不断地被水流搬运至凸岸侧,并且随着时间推移局部淤积和冲刷量不断增加,变化越来越缓慢,最终地形适应水流的变化开始稳定下来,达到平衡冲淤状态。
(2)

(3)
随着数字网络化技术的发展,图书馆的管理模式、服务功能也发生了巨大变化,从单一的静默阅读服务,发展成为团队研讨,为双创发展提供共享学习空间。为此,图书馆办馆方针任务也要随之调整,要打造特色空间、智慧空间,整合文献资源,建设特色资源,提高馆藏利用率,处理好传统文献存储空间与特色共享学习空间的相互依存、相互促进的关系。这也是我们特色建馆的关键。
(4)
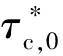
(5)
Z100 3.165 mmol Zn(NO3)2·6H2O溶解于40 mL MeOH/DI混合溶液,25.32 mmol HmIM溶解于20 mL MeOH,前者迅速倒入后者,并持续搅拌120 min。离心操作后于60 ℃真空烘箱中干燥24 h得白色粉末[13]。
弯段相对长度Lc/B=7.85,符合Leopold[16]定义的相对长度<10的自由蜿蜒河道特征,宽度水深之比B/h=8.5,属于相对窄深一类弯道,曲率半径宽度之比Rc/B=2.5,而Zeng[5]认为(Rc/B)<3属于强弯曲渠道,并且参照Vasquez[6]对二次流强度(离心加速度和重力加速度之比)的定义ac/g=0.006,可以认为该弯曲水槽具有比较强的二次流效应,从而对其中的流动和输沙计算带来一定的难度。
(6)
式中β2表示横向底坡。
评定两组患者的疼痛情况,采用VRS 法对患者的疼痛情况进行全面性的评估:Ⅰ级表示为轻度疼痛,对患者的睡眠和生活的不会造成严重性的影响,患者也不需要服用止痛药物;Ⅱ级表示为中度疼痛,患者的疼痛程度比较明显,无法忍受,对患者的生活和睡眠造成了影响,需要服用止痛药物;Ⅲ级表示为重度疼痛,疼痛程度非常剧烈,对患者的生活和睡眠造成了严重的影响,并且还伴随被动体位、自主神经紊乱等现象,需要给予药物止痛。
对于弯曲水槽二次流输沙所形成的横向底坡,其不仅造成输沙方向的偏移,而且还是河床平衡二次流逆底坡输沙,从而达到冲淤平衡的关键因素,本文采用方便实用的Engelund方法[9-10]考虑横向底坡对输沙方向的影响。
(7)
式中:φ表示横向底坡造成输沙方向偏移的角度;∂zb/∂n表示横向底坡;Θ表示Shields数。
3 弯曲水槽试验模拟
3.1 试验布置
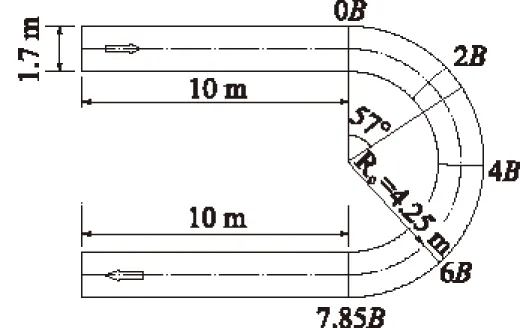
图1 LFM 180°弯曲水槽
应用模型对代尔伏特理工大学(DUT)流体力学实验室(LFM)180°弯曲水槽试验进行模拟[15],通过试验测量与模拟结果的对比验证进一步分析地形平衡冲淤的演化过程。该水槽试验的平面布置如图1所示,试验参数见表1。

表1 LFM 180°弯曲水槽试验参数
在弯曲角度为180°的矩形弯段上游和下游分别连接有长度为10 m的矩形直段,弯段的曲率半径Rc=4.25 m,宽度B=1.7 m,入口处水深h=0.2 m,流速v=0.5 m/s,上游恒定入流量Q=0.17 m3/s,形成的水面坡度为1.8‰,谢才系数C=26.4,弗劳德数Fr=0.36,弯段长度Lc=13.35 m。推移质输沙率qb=0.03 kg/(m·s),试验以推移质输沙为主,沙粒中值粒径d50=0.78 mm,标准偏移σg=1.15,故认为是均匀颗粒泥沙,因此不考虑泥沙的粗化现象,只模拟推移质输沙过程。
会计作为一门应用型学科,其内容从来不是一成不变的。全球经济形势的不断发展,要求会计、审计规则和方法与之相适应,其提供和反映的信息必须更可靠、更合理。人区别于机器和其他生物的最大特征之一在于人类具有优秀的学习实践和创新能力。而会计领域十分强调学习能力,继续教育种类和有关认证考试繁多。只有不断学习掌握高精尖的会计领域专业知识,具备探索和创新精神,才能在人工智能的浪潮中站稳脚跟、不被淘汰。
国外对于步进式直线压电驱动器的研究开始于上世纪六十年代,国内的相关研究略晚于国外,起步于九十年代。多年来,有越来越多的大学和研究机构深入研究了步进式直线压电驱动器,取得了丰富的研究成果。
在弯曲河道冲淤过程中,二次流和河床横向底坡的变化对推移质输沙量和输沙方向起到决定性作用。由弯道弯曲效应所形成的二次流在近床面处将沙粒从凹岸向凸岸输移,从而使凹岸侧地形不断降低而凸岸测地形不断抬升,形成横向底坡,处于底坡上的沙粒又受到自身重力的作用有从凸岸向凹岸滑动的趋势,如此,在二次流逆底坡输沙和沙粒顺底坡重力分量的共同作用下,沙粒在河床上发生运动,直至二者适应当前的水流状态达到平衡为止,此时,地形冲淤即认为达到冲淤平衡状态。
3.2 模拟效果分析
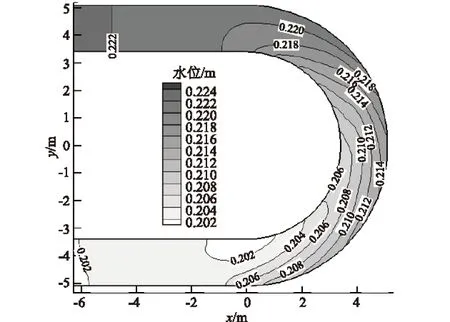
图2 平衡冲淤状态下水位分布等值线
图2为冲淤平衡状态下的水位等值线图,从图2中可以看出在水槽弯曲段凹岸和凸岸有明显的水位差,水流由上游直段进入弯段之后受弯段弯曲效应的影响,在整个弯段内开始出现水面横比降,表现为凹岸水位抬升,凸岸水位降低,并且在弯顶前后水位差达到最大,直至出弯段进入下游直段后,弯段弯曲效应消失,凹岸和凸岸水位迅速恢复至顺直河段水平。
图3为分别距离凸岸和凹岸0.34 m所选取的2个纵向剖面在给定的水流状态下达到冲淤平衡时,计算与测量的相对水深沿程变化对比情况。图中横纵坐标均进行了无量纲化处理。横轴表示弯段相对长度Lc/B,如图1所示,(0~7.85)B为水槽弯曲段,之后为下游直段;纵轴表示相对水深h/h0,h0=0.2 m,相对水深<1表示河床发生淤积,相对水深>1则表示河床发生冲刷,相对水深=1则河床为不冲不淤状态。从图3中可以看出凸岸一侧发生淤积,而凹岸一侧则发生冲刷,其中最大淤积和最大冲刷位置对称分布在弯段(2~3)B之间,此外在弯段与下游直段的交界位置8B前后也有局部的冲淤极值对称分布。数值模拟分别采用Struiksma和Engelund两种考虑推移质导致输沙方向偏移方法,除Struiksma方法有较大差异之外,Engelund方法结果总体上模拟出了剖面沿程的冲淤变化情况,并且除模拟的最大淤积位置稍微靠下游之外,不论是最大冲刷位置还是局部冲淤极值位置都有不错的模拟效果,而且冲淤变化量也基本与试验测量值保持接近。只是在弯段下半段6B前后凸岸侧淤积量和凹岸侧冲刷量均达到最小,模拟结果虽然也体现出了这种趋势,但与测量结果仍然存在一定的差距,尤其以凹岸侧更甚。在出弯段进入下游直段之后(8B之后),凸岸淤积和凹岸冲刷量陡然减少,甚至在接近10B位置凹岸凸岸冲淤态势发生扭转,表现为凸岸冲刷而凹岸淤积,显然,凸岸测的模拟结果要优于凹岸一侧。
式中:ø表示沙粒休止角;β1表示纵向底坡。
考虑地形冲淤所造成的底坡变化对平底河床临界起动切应力的影响,采用Van Rijn的修正公式[11, 14]对平底河床临界起动切应力进行修正
图3 平衡冲淤状态下纵向剖面相对水深计算与测量结果对比
3.3 冲淤演化过程
模型采用非结构化三角形网格,计算区域共划分7 020个三角形单元,3 756个节点。模拟参照表1所示流动和泥沙参数给定相应的初始和边界条件,固壁边界采用滑移不穿透边界条件,为了减少边界条件对流动过程的影响上下游直段均延长至10 m,在上游入口处给定流量边界,下游出口给定常数水位边界,进出口保持试验平衡输沙率0.034 kg/(m·s),糙率n=0.025,计算时间步长Δt=0.01 s,直至480 min后冲淤达到平衡为止,即(∂zb/∂t→ 0)。
由于流动变化的时间尺度小于地形冲淤变化的时间尺度,采用流动和地形冲淤不同时间步的模型不能真实地模拟出河床冲淤演化过程[14],本文流动和冲淤模型采用相同时间步(即在每一个时间步内,计算出流场、悬移质和推移质输沙的变化后,即对地形进行修改,而不是流场和推移质输沙计算若干步之后再对地形进行修改)模拟出平衡冲淤前的河床冲淤演化过程。

图4 地形冲淤演化过程等值线

图5 河床切应力演化过程等值线
不比不知道,一比吓一跳。在茄子移栽后34天,洋丰百倍邦套餐肥展现了强劲效果。观摩会当天,众人冒着高温,在新洋丰工作人员带领下来到茄子示范田。刚进入茄子地,众人就被左右两块茄子地长势差距震惊了,示范田茄子植株明显比对照田要高出一大截。在众人惊奇之余,卢琼珍高兴地为观摩人员介绍示范田和对照田的施肥方案。他一共租80亩地,其中一半转租出去。因卢琼珍是新洋丰肥料零售商,剩余40亩地在新洋丰技术员指导下,施用了百倍邦套餐肥。
图5显示非恒定的河床切应力演化过程,分别包含50,100,200,480 min 4个时刻的床面切应力等值线,表示近河床处的水流强度情况。最大和最小切应力始终对称分布在弯段出口位置,且凹岸一侧大于凸岸一侧,除了弯段内切应力为3等值线不断从靠近凸岸侧偏向凹岸一侧之外,其余等值线随时间变化不十分明显,切应力为3的等值线的迁移过程与弯段内主流从凸岸向凹岸迁移的规律一致。
图6选取试验最大横向坡度发生57°断面的横向地形冲淤演化过程,图中横轴-0.85≤ξ≤0.85,指向凹岸为正,无量化处理表示从凸岸到凹岸的相对距离。从最开始第10 min紧靠凸岸岸壁位置少量的淤积至50 min凸岸淤积量和淤积范围的急剧增长,再到100,200,480 min淤积量和淤积范围变小并且趋于稳定,不冲不淤位置从最初的-0.4迁移至-0.1,且不断向凹岸侧迁移,最终稳定在轴线位置。从图6中同样可以看出,该断面的横向坡度随时间推移越来越大,因为平衡冲淤是在二次流逆底坡输沙和沙粒顺底坡重力分量共同作用下达成,横向坡度的不断增大,代表沙粒重力分量平衡二次流输沙的能力不断增强,最终二次流的逆底坡输沙被沙粒重力分量顺底坡输移作用完全抵消,即达到冲淤平衡状态。
就像文章开头里面提到的一样,过去的一年里,Sarah凭借着超人的毅力迈出了事业家庭双丰收。与此同时,女性葡萄酒专家的身影在葡萄酒行业上也越来越常见。特别是目前在香港常驻的三位MW均为女性,这会是一种巧合吗?
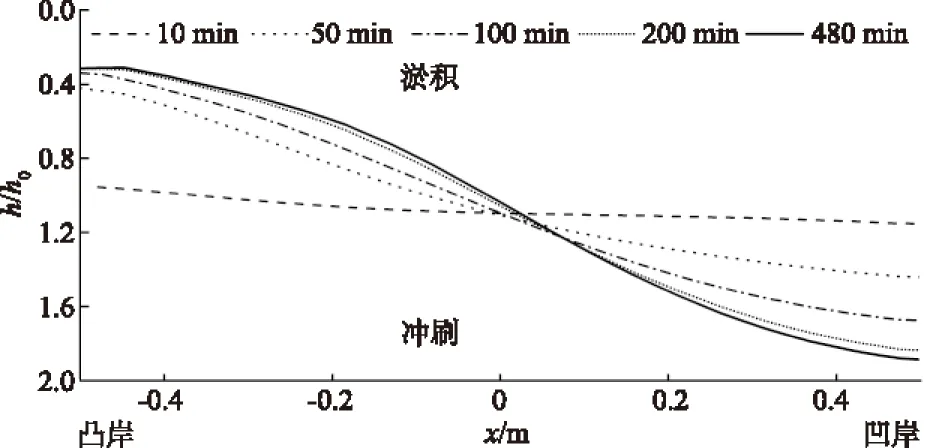
图6 57°断面不同时刻横向相对水深变化过程
4 结 论
文章采用三维水动力和泥沙输运模型模拟弯曲水槽内的三维流动、泥沙输运和内床面冲淤演化问题,直接采用三维模型模拟流动的二次流特性,避免二维模型中对二次流的半经验校正,对于二次流强度较强,横向底坡坡度较大的问题采用Engelund横向输沙模型模拟输沙方向的偏移角度,采用Van Rijn对河床临界起动切应力进行修正,流动和冲淤同步的模拟方法模拟非恒定的地形冲淤演化过程。得到的主要结论有:
(1) 模型成功模拟了180°弯曲水槽的主要冲淤特性,基于非结构化网格的三维地形冲淤模型在实际蜿蜒河道的数值模拟中有广阔的应用前景。
(2) 对于强弯曲、横向底坡较大的水槽冲淤问题,不需人为指定参数,方便实用的Engelund横向输沙模型以及考虑对河床临界起动切应力进行修正方法的应用,能取得不错的模拟效果。
礼貌和不礼貌的研究倾向于忽略面子威胁目标对象的回应。话语分析者进行语篇分析时,揭示了受话人对于不礼貌的回应关系到对话的进展。因此,Culpeper et al.(2003)提出了语篇分析中不礼貌话语回应策略的框架。
(3) 三维流动和地形冲淤相同时间步计算的模型能有效地模拟出非恒定的地形冲淤过程,有助于认识冲淤平衡前的地形演化过程。
参考文献:
[1] 吴持恭,水力学[M].北京:高等教育出版社, 2003.(WU Chi-gong.Hydraulics[M].Beijing: Higher Education Press, 2003.(in Chinese))
[2] 张武红, 吕 昕.弯道水力学[M].北京:水利电力出版社, 1993.(ZHANG Wu-hong, LV Xin.Hydraulics of Curved Channel[M].Beijing: Water Resources and Electric Power Press, 1993.(in Chinese))
[3] 董耀华.弯道水流的基本特性及数值模拟[J].长江科学院院报,1996,13(1): 25-29.(DONG Yao-hua.Essential Features and Numerical Modeling of Bend Flow[J].Journal of Yangtze River Scientific Research Institute, 1996, 13(1): 25-29.(in Chinese))
[4] 赵根生,卢金友,汪 鹏.连续弯道演变机理研究综述[J].长江科学院院报,2009,26(6): 1-3.(ZHAO Gen-sheng, LU Jin-you, WANG Peng.Review on Research for Evolution of Continuously Curved Channels[J].Journal of Yangtze River Scientific Research Institute, 2009, 26(6): 1-3.(in Chinese))
[5] ZENG J, CONSTANTINESCU G, WEBER L.A 3D Non-hydrostatic Model to Predict Flow and Sediment Transport in Loose-bed Channel Bends[J].Journal of Hydraulic Research, 2008,46(3): 356-372.
[6] VASQUEZ J A, MILLAR R G, STEFFLER P M.River2D Morphology, Part II: Curved Alluvial Channels[C]∥Canadian Society for Civil Engineering(CSCE).17th Canadian Hydrotechnical Conference, Edmonton, Alberta, August 17-19, 2005: 259-268.
[7] ZENG J, CONSTANTINESCU G, WEBER L.Prediction of Equilibrium Flow and Bed Load Transport in a Curved Bend[C]∥American Society of Civil Engineers(ASCE) World Environmental and Water Resource Congress Omaha, Nebraska, United States[J].May 21-25, 2006: 1-11.
[8] 邢 岩, 金 生, 艾丛芳, 等.明渠弯道三维冲淤数值模拟[J].泥沙研究,2013,(6): 1-5.(XING Yan, JIN Sheng, AI Cong-fang,etal.Three-dimensional Numerical Modeling of Bed Evolution in Open Channel Bends[J].Journal of Sediment Research, 2013, (6): 1-5.(in Chinese))
[9] ENGELUND F.Flow and Bed Topography in Channel Bends[J].Journal of the Hydraulics Division,1974,100(11): 1631-1648.
[10]RUTHER N, OLSEN N R.Three-dimensional Modeling of Sediment Transport in a Narrow 90 Channel Bend[J].Journal of Hydraulic Engineering, 2005,131(10): 917-920.
[11]DUAN J G, JULIEN P Y.Numerical Simulation of the Inception of Channel Meandering[J].Earth Surface Processes and Landforms, 2005, 30(9): 1093-1110.
[12]邢 岩, 艾丛芳, 金 生.强弯渠道三维水流数值模拟.水道港口[J].2013,34(4): 335-343.(XING Yan, AI Cong-fang, JIN Sheng.Three-dimensional Modeling of Flow in a Sharp Open Channel Bend[J].Journal of Waterway and Harbor, 2013, 34(4): 335-343.(in Chinese))
[13]WU W.Computational River Dynamics[M].London: Taylor & Francis, 2008.
[14]KHOSRONEJAD A, RENNIE C D, SALEHI N S,etal.3D Numerical Modeling of Flow and Sediment Transport in Laboratory Channel Bends[J].Journal of Hydraulic Engineering, 2007,133(10): 1123-1134.
[15]STRUIKSMA N, OLESEN K W, FLOKSTRA C,etal.Bed Deformation in Curved Alluvial Channels[J].Journal of Hydraulic Research, 1985,23(1): 57-79.
[16]KASSEM A A, CHAUDHRY M H.Numerical Modeling of Bed Evolution in Channel Bends[J].Journal of Hydraulic Engineering, 2002,128(5): 507-514.

