端锚粘结式锚杆受力特性试验研究

，，，

(辽宁工程技术大学 土木与交通学院，辽宁 阜新 123000)

到目前为止，研究在全锚条件下锚杆体的受力机制成果有很多[1-5]，但仅有较少系统的文献研究过端锚粘结式锚杆体锚固段的受力特性，且大多数研究不能正确反映锚杆体的实际受力特性。伴随着外载荷数值水平的持续增大，杆体和周围灌浆介质交界面上的微观粘结剪切应力也随着增大，而且最大剪切应力的峰值渐渐地向锚固段的底端传递，最终端锚段的全部灌浆体材料完全进入到塑性变形模态[6-8]。

本文主要以水泥水玻璃砂浆端锚锚杆体为研究对象，采取小应变高频动荷载可等效成大应变低频荷载的加载模式，进行反复拉拔试验，得出在不同的外载荷作用下，端锚锚杆在锚固段各位置处拉应力与剪切应力变化趋势，为其工程应用提供理论支撑。

1 试验设计

1.1 试验材料

此次端锚锚杆力学模型试验采用光圆钢筋进行粘结拉拔试验，对于所采用的圆钢钢筋应该按照《金属材料室温拉伸试验方法》(GB/228—2002)进行材料的各种弹性和塑性指标参数的试验，各详细参数具体见表1。为了加快试验进程，改善砂浆的凝固时间和提高强度，试验的灌浆材料采用CS水泥水玻璃砂浆。水泥和水玻璃选用根据《建筑工程水泥-水玻璃双液注浆技术规程》(JGJ211—2010)的行业标准来确定。试验采用阜新市生产的大鹰牌强度为42.5R普通硅酸盐水泥和模数2.4～3.4，浓度为30°Be～45°Be的水玻璃，水泥和水玻璃的比例为1∶1，温度24 ℃。根据不同水灰比下CS浆液的凝结时间强度参数[9]，选择水灰比为0.5∶1，水玻璃选择浓度为45°Be，强度等级相当为M20，试验所用的水为洁净自来水。

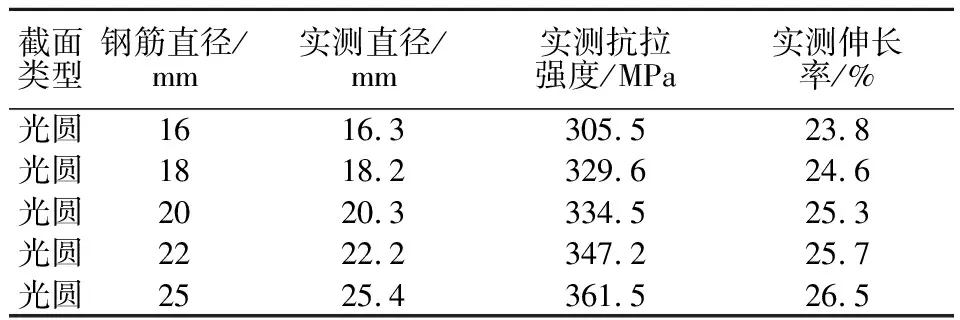
表1 钢筋材料参数

1.2 模型设计及制作

模型试验采用DN150型热镀锌管，直径为15.24 cm，钢号为Q235，作为承载岩体，CS砂浆作为锚固剂或是灌浆介质，光圆钢筋来代替锚杆，在这里特定假设承载岩体和锚杆体均为各向同性、均匀分布的介质。钢筋锚固段具体设计长度及其对应钢管设计长度数据见表2。端锚锚固模型试样和养护试样见图1。

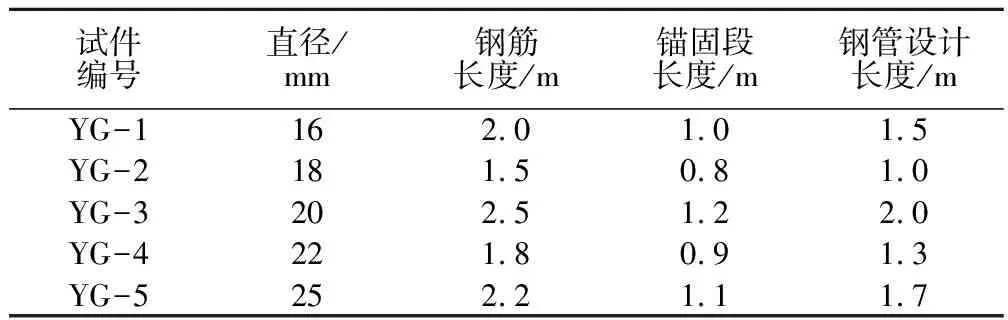
表2 锚固段设计长度和钢管设计长度

图1 端锚锚固模型试样

1.3 试验装置与测试系统

本试验采用DN150型热镀锌管(外径为15.24 cm)来模拟承载岩体，CS浆液来模拟锚固剂，端部焊接与之相垂直120 mm长短钢筋头的光圆钢筋来模拟锚杆。研究端锚粘结式锚固段力学特性机理的模型试验测试中，主要采用小应变高频动荷载等效成大应变低频荷载的手段，试验可通过静载拉拔仪进行反复加载、卸载来完成。试验测试系统如图2所示，信号流程如图3所示，模型试验设备分为2个部分：

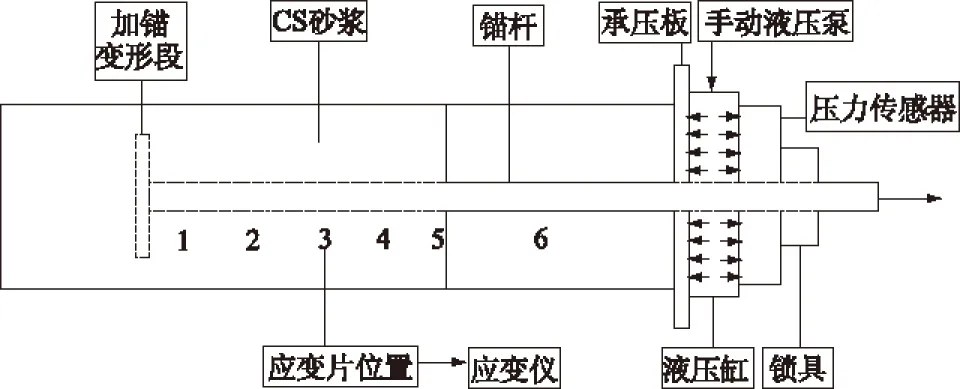
图2 端锚锚杆试验测试系统示意图

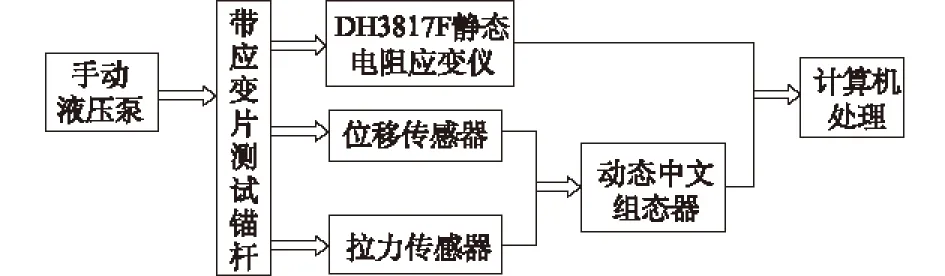
图3 测试系统信号流程图

图4 模型加载系统

(1)加载系统。直接采用XHYL-60 锚杆综合参数测定仪进行加载，主要包括手动泵(工作压力63 MPa)、液压缸(最大行程120 mm，额定拉力500 kN)、圆环压力传感器(测量范围0～500 kN)、位移传感器(测量范围0～50 mm)、智能中文组态器及带快速接头的高压油管等组件。在实际井巷开采过程中动荷载大多数为小应变高频荷载，作用于锚杆上形成小应变，随着时间的累积，小应变逐渐累加形成大的应变破坏，因此本文采用小应变高频动荷载等效成大应变低频荷载的原理，加载装置如图4所示。具体加载的荷载等级和时间见表3，其中初始荷载为0。本试验是在动荷载作用下完成的室内模型试验，故本文中没有说明的地方均是代表动应力、动位移，轴向应力为动应力峰值。

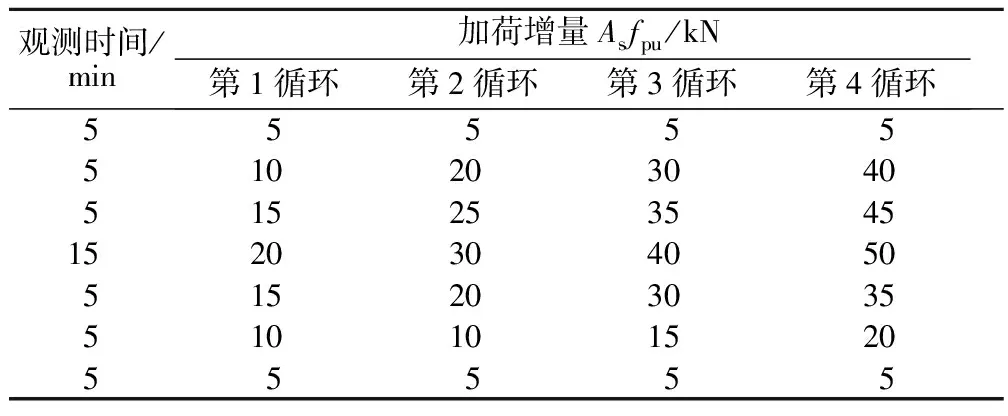
表3 锚杆极限抗拔试验的加载等级和观测时间

注：As，fpu分别为钢筋的横截面积和极限抗拉强度。

每个试件钢筋极限拉拔力如表4所示。

表4 钢筋极限拉拔力

(2) 测试系统如图2所示，采用10通道的静态应变仪对端锚钢筋上粘贴的应变片进行应变测量。测试系统包括数据采集箱、计算机和支持软件，采样率为1 kHz，测试范围是±19 999×10-6。

2 试验结果与分析

按照小应变高频动荷载的试验原理进行端锚模型试验，进行4次反复加卸载的循环试验，按照加载增量值与时间的关系，并结合Origin软件自带SineDamp波形图函数，求解出自身函数模型的形式,即

(1)

式中：P为荷载增量；t为荷载加载时间(min)；P0，A，b0，tc和ω为需要采用Origin软件对加载增量与加载时间进行非线性拟合分析确定的待定系数。

拟合分析出待定系数分别为P0=2.17×10-4，A=0.261，b0=241.27，tc=-89.834，ω=45.099，则拟合之后的非线性函数模型为

按照图5所示的加载方式，可计算求解出YG-1，YG-2，YG-3，YG-4和YG-5试件各自的加载应力波形函数模型，并测得锚杆沿轴线方向的应变大小，单位为10-6的数量级。图中的负数不代表压力，只是为能够更好地体现加卸载循环效果，将2，4等循环变成负数来表现，能够拟合出非线性波形函数，在以下图中出现的负数均是该表达方式，不再赘述。不同外载荷反复循环的作用下，5个锚杆试件的应力波函数和锚杆应力沿轴向的分布情况如图6所示。其中，图6中波峰、波谷代表加卸载循环，故应力波形图的第2个波谷与轴向应力分布图的第4次循环是对应关系；且每次循环按照表3的荷载增量进行加载，故正常一个循环应有7条直线，但有时候的直线也会重合。轴向应力分布图中，轴向长度小于800 mm的为锚固段，大于该范围的为自由变形段。

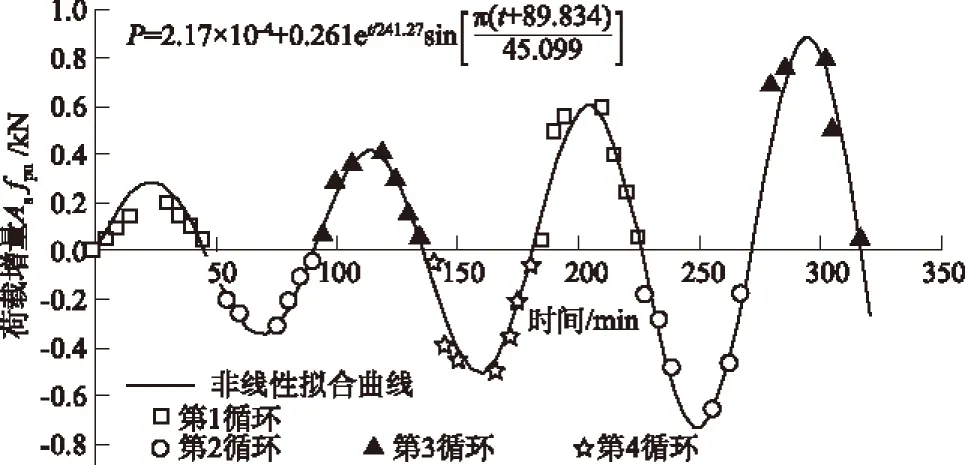
图5 模型试验加载情况

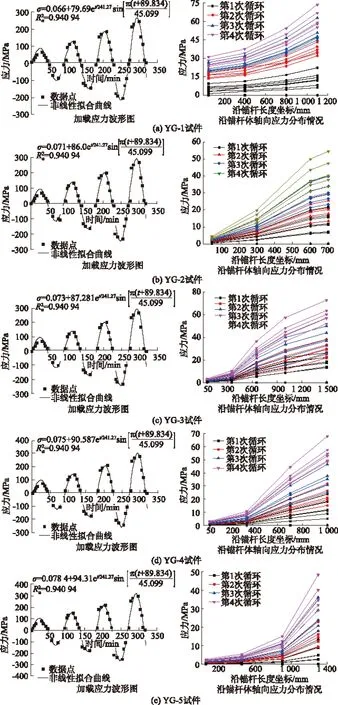
图6 5个锚杆试件的加载应力波形图及沿锚杆体轴向应力分布情况

通过分析图6可知，加载增量与时间的非线性函数模型公式(1)中，参数P0与A是随着加载数据变化的，参数b0，tc和ω不伴随着加载数据大小和形式改变，变成常数项，取值为b0=241.27，tc=-89.834和ω=45.099，从而可将模型函数改写成：

(2)

从公式(2)和波形图可得出，含有正弦函数sin项，波形呈现出周期性，可计算出周期T1=2π/ω=0.139 246，注意此时单位为“分”，通常单位为“s”，在这里进行换算取T=T1/60=0.002 320 8 s，频率f=1/T=430.882 Hz，同时这也验证本文研究的小应变高频动荷载加载模式的正确性和可靠性，可满足端锚模型试验要求。类似为端锚自由变形段的应力应变值最大，产生波峰值，在锚固段远端产生波谷值，最小值有的可以接近0。这个在小应变高频反复循环载荷作用下沿锚杆体轴向产生的应力分布近似为正弦函数的λ/2波长之间的波形图，并且波峰逐渐向锚固段的远端缓慢传播，只不过正弦函数图形是伴随着时间周期T传播，而此时是利用在4次小应变高频动荷载作用下，促使应力应变波波形逐渐向端锚锚固段的底端传播；伴随着端锚杆体锚固段长度的增加，锚固段和自由段的应力值也随之增大，且在锚固段的应力波形逐渐趋于平缓，变化率缓慢减小，在自由变形段的应力应变波形的变化率则出现陡增的情况，波形变得陡峭。根据规范和模型试验实际结果算出每个试件的破坏荷载值见表5。

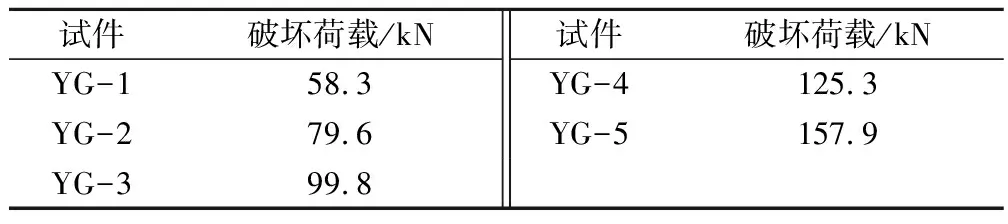
表5 锚杆极限抗破坏荷载

因应变为已知条件，按照力学理论的平衡条件[10]，从而推算出相邻2个测点间粘结平均剪切应力，此处假设端锚锚杆体在锚固段远端的宏观与微观的力学特性均为0，故可以认定锚杆体远端的平均剪切应力为0。具体平均剪切应力的算法见式(3)。

(3)

式中:E为锚杆弹性模量；εa为锚杆体在a点位置处微观应变值(%)；εb为锚杆体在b点位置处微观应变值(%)；r为锚杆体半径(mm)；d为锚杆体直径(mm)；lab为相邻2个测点之间的相对距离(mm)。从而计算出端锚锚杆体在小应变高频的反复循环卸载情况下的平均剪应力分布情况，如图7(a)所示。这里主要选取具有代表性YG-4试件进行分析，以下的位移计算和剪应力-位移曲线分析都是取YG-4试件。

利用微积分的几何定义可知，按照轴向应变与轴向位移的关系，假设沿轴向应变在2个微小测点单元之间为梯形分布，可将2个测点之间应变分布进行简化处理，进而可以推导出端锚锚杆体轴向各点的宏观位移分布情况。可以利用式(4)进行计算。

(4)

式中：ui为锚杆体在i点位置处的宏观位移(mm)；εi，εi-1分别为锚杆体在i，i-1点位置处的微观轴向应变(%)；Δlj为相邻2个测点之间的相对长度，可以理解为积分步长(mm)。从而计算推导出端锚锚杆体在小应变高频的反复循环卸载情况下的宏观位移分布情况，如图7(b)所示。

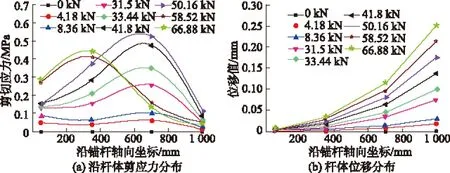
图7 不同荷载下沿杆体剪应力及位移分布

从图7中可以看出，在外施加荷载较小的情况下，锚杆体均处于线弹性的工作状态，主要受到锚固段近端的灌浆材料与钢筋之间的粘结剪切应力来抵抗，此时在自由变形阶段与锚固段交界处的锚杆体剪切应力取得峰值，位移峰值在自由变形段产生；伴随着外载荷数值的逐渐增加，沿锚杆体剪切应力也逐渐增大，同时逐渐出现向锚固段底端传递的现象，当施加外载荷达到58.52 kN和66.88 kN时沿锚杆体剪切应力的传递性现象比较显著；当外载荷继续增大，剪切应力的峰值直至锚固段底端，同时峰值大小逐渐减小，而且灌浆体和锚杆体之间产生滑移现象，只能是依靠两者之间的摩擦力来抵消二者的相对运动。为分析端锚锚杆沿轴线方向剪切应力与滑移产生的位移之间的力学关系，将图7(a)和7(b)中沿锚杆体的剪切应力和位移进行简单的数据处理，绘制出在不同外载荷的作用下剪应力-位移曲线，即τ-u曲线，详见图8。

分析图8可知，在沿锚杆体轴向位移较小的情况下，在一定范围内端锚锚杆体的剪切应力与轴向位移近似可看成是线性关系；伴随着轴向杆体位移的逐渐增大，剪切应力也逐渐达到最大极限值；当位移值达到最大极限值后，随着位移的继续增加，沿YG-4圆钢试件杆体的剪切应力逐渐减小，最终产生一定数值的残余剪切微观应力值，换句话说是沿端锚锚杆体的任意某一特定位置处的微观本构关系并不是完全的线弹性关系。在这里引入一个变刚度的概念，将其定义为τ-u曲线的斜率变化情况的一个度量，它隶属于线弹塑性本构关系的范畴；在位移值处在较小的范围内时，各位置处的曲线斜率变化情况较为相似，在一定程度上可以认为是起初变刚度是相同的。但是各个测点位置处的峰值情况是不同的。位置3处的剪切应力和变刚度的峰值都是最大的，位置4处的2个峰值情况是最小。造成这一现象的原因是由于本次试验为了加大锚固力，特在锚固段底端位置处加焊接一个直径为120 mm的钢筋棍，来更加真实地模拟锚杆的实际受力特性情况，导致锚固段底端灌浆体介质受到的约束力大于自由变形段的约束力。

3 结 论

(1) 对4次反复加卸载方案进行非线性模型分析,并通过拟合验证本文研究的小应变高频变动荷载的加载模式的正确性和可靠性，可满足端锚模型试验要求。

(2) 结合各自试件应力波形函数研究分析，在加载频率为430.882 Hz情况下，端锚自由变形段的应力应变的数值最大，在锚固段远端产生波谷值，最小值有的可以接近0，沿锚杆体轴向产生的应力分布近似为正弦函数的λ/2波长之间的波形图，并且波峰逐渐向锚固段的远端缓慢传播，只不过正余弦函数图形是伴随着时间周期传播，而此时是随着锚杆长度传递。

(3) 通过试验结果处理分析可求解出沿锚杆体的剪切应力分布、位移情况曲线和τ-u曲线，在端锚锚固变形段的剪应力取得较大值，同时伴随着循环加卸载增量百分比和次数的增加，剪切应力峰值发生传递性，逐渐缓慢向锚固段底端的方向移动，最终导致锚固段的锚固特性失去工作效能。

参考文献：

[1] 高大水，吴海斌，王 莉. 三峡船闸高边坡预应力锚索耐久性研究[J]. 岩土力学，2005，26(增2)：126-135.(GAO Da-shui，WU Hai-bin，WANG Li. Research on Endurance of Prestressed Anchorage Cables in TGP Shiplock’s High Slope[J]. Rock and Soil Mechanics，2005，26(Sup.2)：126-135. ( in Chinese))

[2] JARRED D J，HABERFIELD C M. Tendon/Grout Interface Performance in Grouted Anchors[C]∥Proceedings of Ground Anchorages and Anchored Structures. London: Thomas Telford, 1997: 256-263.

[3] KILIC A，YASAR E，ATIS C D. Effect of Bar Shape on the Pull-out Load Capacity of Fully Grouted Rock Bolt[J]. Tunnelling Underground Space Technology，2002，18(1)：1-6.

[4] 秦 强，尹健民，吴从清，等. 锚杆声波反射法质量检测的模拟试验研究[J]. 长江科学院院报，2011，28(8)：41-45. (QIN Qiang，YIN Jian-min，WU Cong-qing，etal. Simulation of the Application of Sonic Reflection Method in Rockbolt Anchorage Quality Detection[J]. Journal of Yangtze River Scientific Research Institute，2011，28(8)：41-45.( in Chinese))

[5] 姚显春，李 宁，陈蕴生，等. 隧洞中全长黏结式锚杆的受力分析[J]. 岩石力学与工程学报，2005，24(13)：2272-2276. (YAO Xian-chun，LI Ning，CHEN Yun-sheng，etal. Theoretical Solution for Shear Stresses on Interface of Fully Grouted Bolt in Tunnels[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(13)：2272-2276. ( in Chinese))

[6] 肖国强，吴基昌，周黎明，等. 锚杆质量无损检测中的缺陷信息提取方法研究[J]. 长江科学院院报，2012，29(11)：73-76. (XIAO Guo-qiang，WU Ji-chang，ZHOU Li-ming，etal. Method of Extracting Defective Information in Non-destructive Detection of Anchor Quality[J]. Journal of Yangtze River Scientific Research Institute，2012，29(11)：73-76. ( in Chinese))

[7] 赵 林，曾宪明，李世民，等. 优化复合锚固结构与单一锚固结构抗爆性能对比试验研究[J]. 岩土力学，2011，32(10)：3019-3025. (ZHAO Lin，ZENG Xian-ming，LI Shi-min，etal. Comparative Test Study of Blast-resistance Performance of Optimal Composite Anchorage Structure and Single Anchorage Structure[J]. Rock and Soil Mechanics，2011，32(10)：3019-3025. ( in Chinese))

[8] 李术才，张 宁，吕爱钟，等. 单轴拉伸条件下断续节理岩体锚固效应试验研究[J]. 岩石力学与工程学报，2011，30(8)：1579-1586. (LI Shu-cai，ZHANG Ning，LV Ai-zhong，etal. Experimental Study of Anchoring Effect of Discontinuous Jointed Rock Mass under Uniaxial Tension[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30(8)：1579-1586. (in Chinese))

[9] 赵明华，王海波，刘晓明，等. 红层锚杆抗拔力学性质模型试验研究[J]. 湖南大学学报(自然科学版)，2013，40(8)：1-5. (ZHAO Ming-hua，WANG Hai-bo，LIU Xiao-ming，etal. Model Test Research on the Red Layer Anchors，Mechanical Properties of Pullout Resistance[J]. Journal of Hunan University(Natural Science)，2013，40(8)：1-5. (in Chinese))

[10] 梁广昌. 简谐波作用下锚杆数值模拟分析[D]. 广州：广东工业大学，2013. (LIANG Guang-chang. Numerical Simulation Analysis on the Anchor Bolts under Simple Harmonic Wave[D]. Guangzhou：Guangdong University of Technology，2013. (in Chinese))