基于聚类分析的客户用电模式智能识别方法

彭显刚1，赖家文1，陈 奕2



基于聚类分析的客户用电模式智能识别方法

彭显刚，赖家文，陈 奕

(1.广东工业大学自动化学院，广东 广州 510006；2.广东电网公司湛江供电局，广东 湛江 524005)

结合k-means、k-medoids、SOM以及FCM等聚类算法，构建了电力大客户典型用电模式的聚类分析模型，提出了一种评估聚类效果的新方法。首先通过分析电力客户用电指标数据及其特点，提出采用高斯滤波器对含“噪声”曲线数据进行平滑处理来获取客户用电数据。然后提出了聚类平均半径、平均直径和平均最小间距等3个评价指标，并以此为基础设计出一种评估聚类得分的新方法。最后使用聚类分析模型对某地区电力大客户日用电量曲线进行聚类分析，实现了地区典型用电模式的自动识别功能。实际算例分析结果表明，该评估方法物理概念清晰、简便、实用。

用电模式分析；高斯核函数平滑；聚类效果评估；聚类分析

0 引言

挖掘与统计分析辖区内电力大客户的用电模式有利于供电部门掌控用电群体构成及其用电特性，实现客户的精细化管理，提供优质的用电服务。对电力市场营销、客户精益化管理和智能用电服务等方面具有重要意义。

在负荷模式识别领域中，研究者们普遍赞同4条标准：1）每个用电模式代表一类相似的用电群体；2）各模式间应能够相互区别；3）模式判别的方法应当是易执行的；4）聚类数应适中，用电模式的数量不能太多。目前聚类分析在电力系统中的应用研究已涌现出大量研究成果。然而，当前所提出的各种方法难以满足实际应用中的要求，主要原因如下：首先，若以用电指标区分客户群体，辖区内客户群的种类未知；第二，用电数据一般为高维数据，低维聚类分析中聚类效果评估方法在高维数据中显得不再适用，缺乏确定群体数的有效方法；第三，客户用电指标数据中往往存在“噪声”，而它对聚类质量的影响是较严重的，应采取有效措施进行处理。

本文针对上述研究的不足，提出了一种评价高维曲线聚类的有效方法；以高斯滤波技术消除原始数据中的噪声，结合k-means、k-medoids、SOM以及FCM等聚类算法构建聚类分析模型；对大量电力大客户的用电数据进行分析统计，获取隐藏在数据集中典型用电模式及其合适的聚类数目。

1 数据准备

1.1用电指标数据的特点

用电指标数据来源于已建成的一系列和电能信息采集相关的系统，其特点有以下几方面：1）电力客户的用电指标数据类型较多，大量指标数据组成´的高维数据矩阵，其结构为对象－用电指标，为对象的个数，为用电指标的维度；2）客户用电指标数据有两个重要特征：相似性与波动性，相似性与文献[14]提出电力负荷曲线相似性定义是一致的，波动性是指客户投入或切除大功耗用电设备时，用电曲线产生形状变化；3）客户用电数据是高维的且时序相关，是反映客户用电行为或用电习惯的指标数据；4）客户用电数据中存在“噪声”，导致用电曲线不平滑，影响聚类效果；5）客户用电数据量较大，而在数据统计层面上典型用电模式的数量相对而言较少。

1.2 数据预处理

在数据分析前应采取以下数据预处理步骤：

a）求取客户多日同时刻数据均值组成用电特性曲线作为原始数据，并采用高斯滤波对客户用电特性曲线进行曲线平滑处理。高斯滤波以高斯核函数曲线形状选择权值对曲线进行线性平滑滤波，该方法对去除服从正态分布的噪声颇具效果。设原始数据为个客户的日平均用电指标数据矩阵，平滑处理后，其中；方差与窗宽为可调参数。

高斯核函数表达式为

方差决定函数曲线的扁平程度。越小，曲线越陡峭；越大，曲线越扁平。窗宽决定参与平滑处理的原始数据个数。一般地，取值小于1；取单数，小于等于5。

以下为高斯平滑的过程：

定义窗宽Î，则

接着求取系数矩阵，其表达式为

对原始数据进行补位操作组成新的数据矩阵¢，即将的1至ë/2û列和-ë/2û+1至列分别补到的最后和最前得到¢，¢中行向量d¢如式(4)所示，再¢中每一行向量d¢与进行卷积，得=[¢,¢,,¢,,¢]Î^(+2/2+-1)，截取中间的´矩阵作为，中第行第列数据d表达式为

(5)

(6)

其中：Î[1,+2´ë/2û+-1]；Î[1,]，ë/2û为向下取整。

高斯平滑处理效果如图1所示。

图1曲线的高斯平滑处理

b）数据标准化。用公式(7)对进行标准化。

2 聚类分析模型

2.1聚类算法的选择

聚类算法多种多样，并非所有都适用于分析用电指标数据。按算法设计思路可分为：划分方法、层次方法、基于密度方法、基于网格方法和基于模型方法。基于密度方法在抵抗异常数据方面的能力较强，并且能够处理任意形状和大小的类簇；但是，当算法相关参数设置不当或类簇密度变化明显时，聚类会遇到问题；而且，难以定义与计算高维数据的密度。基于网格方法的网格单元个数随着数据维度增加而爆炸性增长，且网格单元包含单个对象的情况很容易发生，导致较差的分析效果。因此，本文不予考虑这两种方法，选择划分方法中k-means、k-medoids和FCM以及基于模型方法中SOM作对比分析。另外，选用欧氏距离（Euclid Distance）作为对象间距的度量：

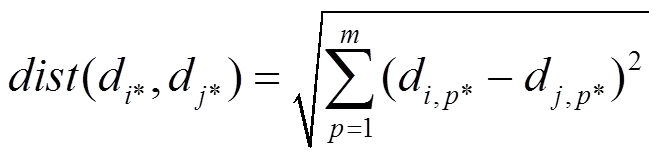
2.2 聚类效果评估

2.2.1基本评价指标定义

在此先介绍本文提出的三个基本评价指标：

定义1聚类平均半径是指当前聚类结果中各个类簇内对象与类簇中心的最大距离之和的平均值。聚类平均半径定义为

定义2聚类平均直径是指当前聚类结果中各个类簇内对象之间的最大距离之和的平均值。聚类平均直径定义为

(10)

定义3聚类平均最小间距是指当前聚类结果中各个类簇内所有对象与其余对象之间最小距离之和的平均值；特别地，当聚类数为1时，聚类平均最小间距为0。聚类平均最小间定义为

式(9)~式(11)中：为聚类数；C为第个类簇；Î[1,]；r为第个类簇的聚类半径；d为第个类簇的聚类直径；b为第个类簇的聚类最小间距；`x为C类的类簇中心。

2.2.2 评估方法

聚类分析主要为了达到两个指标：a）类簇内尽可能紧凑，b）类簇间尽可能区分明显。实现评估聚类效果的方法也将从这两方面切入，以聚类平均半径或聚类平均直径评价类簇内的紧凑性，以聚类平均最小间距评价类簇间差异。然而单独以一个评价指标难以从整体上评价聚类效果，必须有机地将两个评价指标结合对当前聚类结果作出综合评估，以确定当前聚类数是否合适。本文提出以式(12)和以式(13)分别求取聚类效果评价得分1和得分2。

(13)

式中：为聚类个数；为数据集中对象的个数。

2.2.3 有效性验证

以IRIS数据集为例。该数据集是在数据挖掘、数据分类中常用的测试集、训练集，以鸢尾花的特征作为数据来源，每个数据对象包含4个属性，总共150个数据对象，分为3类，每类50个数据对象，分别为setosa、versicolor和virginica。

现以k-means聚类算法对IRIS数据集进行聚类，并计算对应聚类数下的聚类平均半径、聚类平均直径和聚类平均最小间距，绘制成图2(a)~2(c)。

图2 IRIS数据集的均值聚类效果评估

Fig. 2 IRIS dataset clustering evaluation of k-means

在大于8时聚类平均半径（直径）将不会出现较大的变化；在2≤≤5时，聚类平均最小间距曲线上的尖峰状脉冲表明在其出现的聚类数范围内的聚类结果区分度是最明显的。各个值下的得分1与得分2评估结果绘制成图2(d)和图2(e)，得分越高聚类效果越好。

表1列举出2≤≤8内k-means与k-medoids聚类算法的得分情况，表明不同的聚类结果、不同的聚类算法将得到不同的评价结果。数据显示将IRIS数据集分2~4类较合适，符合实际情况。

表1评估聚类效果得分

Table 1 Scores of IRIS dataset clustering evaluation

2.3 聚类分析模型

评估聚类效果的关键在于计算聚类结果内部的紧凑性和外部的区分度，本文在聚类分析中加入评价聚类效果的环节，分析模型图3所示。聚类过程未知对象集中群体的个数，是一个无监督的学习过程。在以往的聚类分析中，聚类数需分析人员根据一定的方法给出，但缺乏有效的聚类评估方法，难以准确地定位最优的聚类数。图3模型中，从聚类分析的输入变为输出；为防止模型过度计算，分析过程外加限制条件：<。通常，最优聚类数远远小于对象总数，只要选择合适的就能将最优的聚类数涵盖在分析过程里面。

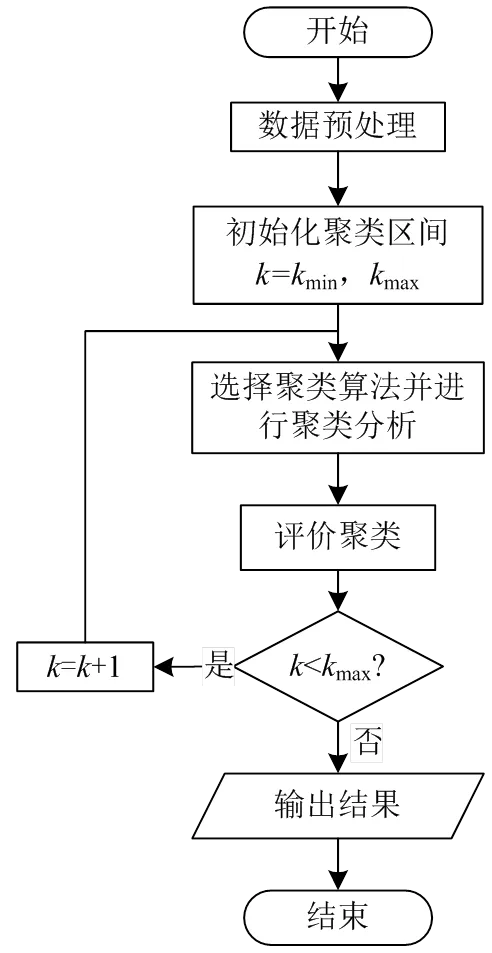
图3 聚类分析模型流程图

3 应用实例

下面使用上述聚类模型，结合k-means、k-medoids、SOM以及FCM等聚类算法分析2011年某地区2 629户电力大客户的24点日电量曲线数据，以式(12)评估值为评估结果，结果如表2。

限于篇幅，本文只列出k-means与FCM两个聚类模型的聚类簇，如图4、图5所示。

在此附上基于k-means模型聚类数从2到15的评估结果，如表3。

表2中结果表明FCM聚类模型是最稳定的；表3中结果表明k-means模型分为6~9类是合适的；同理，笔者由实例结果得出k-medoids模型分为10~12类，SOM模型分为12~15类，FCM模型将数据集分为4类是最合适的。

另外，采用常用的MIA(mean index adequacy)指标进行聚类效果评估对比，MIA指标表征类簇内对象与类簇中心的平均距离，越小的MIA值表明聚类效果越好。如图6所示，k-means、k-medoids和SOM模型的MIA值出现了与前文所述的相似评估效果，但在MIA曲线整体上难以准确定位最优的聚类数区间；对FCM模型来说MIA指标失效，得出与前文实验相反的结果。

表2聚类分析结果

Table 2 Results of several clustering algorithms

表3聚类数为2~15的k-means聚类评估结果

Table 3 Scores of 2~15 clusters based on k-means

图4 k-means聚类簇

Fig. 4 Clusters of k-means

图5 FCM聚类簇

图6 MIA指标评估结果

综合上述分析结果，该地区的典型用电模式应分为4~15类。从图4、图5聚类簇的形状和数量分布方面上看，每种聚类算法得出的聚类结果都具有一定的合理性。如，k-means聚类模型分为7类时，每个类簇有着明显的区别，用电量峰值、峰值出现时段以及基础负荷等都不相同；FCM模型则更具归纳性地将数据分为4类，主要类型为双峰型、高负荷率型以及避峰型等。

4 结语

本文以数据挖掘的一般过程为技术线路，以聚类分析为基础，结合基于聚类平均半径、聚类平均直径和聚类平均最小间距的聚类评价指标，构建了基于k-means、k-medoids、SOM以及FCM等聚类算法的聚类分析模型，实现了对数据集的智能化聚类的分析功能，具有较高的实用价值。基于本文方法开发的实际系统已经应用于客户用电智能化分析系统之中。

[1] 廖志伟, 孙雅明. 数据挖掘技术及其在电力系统中的应用[J]. 电力系统自动化, 2001, 25(11): 62-66.

LIAO Zhi-wei, SUN Ya-ming. Data mining technology and its application on power system[J]. Automation of Electric Power Systems, 2001, 25(11): 62-66.

[2] 黄宇腾, 侯芳, 周勤, 等. 一种面向需求侧管理的用户负荷形态组合分析方法[J]. 电力系统保护与控制, 2013, 41(13): 20-25.

HUANG Yu-teng, HOU Fang, ZHOU Qin, et al. A new combinational electrical load analysis method for demand side management[J]. Power System Protection and Control, 2013, 41(13): 20-25.

[3] 周开乐, 杨善林. 基于改进模糊C均值算法的电力负荷特性分类[J]. 电力系统保护与控制, 2012, 40(22): 58-63.

ZHOU Kai-le, YANG Shan-lin. An improved fuzzy C-means algorithm for power load characteristics classification[J]. Power System Protection and Control, 2012, 40(22): 58-63.

[4] CHICCO G. Overview and performance assessment of the clustering methods for electrical load pattern grouping[J]. Energy, 2012, 42(1): 68-80.

[5] 黎祚, 周步祥, 林楠. 基于模糊聚类与改进BP算法的日负荷特性曲线分类与短期负荷预测[J]. 电力系统保护与控制, 2012, 40(3): 56-60.

LI Zuo, ZHOU Bu-xiang, LIN Nan. Classification of daily load characteristics curve and forecasting of short-term load based on fuzzy clustering and improved BP algorithm[J]. Power System Protection and Control, 2012, 40(3): 56-60.

[6] BAILEY J. Load profiling for retail choice: examining a complex and crucial component of settlement[J]. The Electricity Journal, 2000, 13(10): 69-74.

[7] TSEKOURAS G J, KOTOULAS P B, TSIREKIS C D, et al. A pattern recognition methodology for evaluation of load profiles and typical days of large electricity customers[J]. Electric Power Systems Research, 2008, 78(9): 1494-1510.

[8] 张粒子, 蔡学文, 鲁宇, 等. 面向错峰潜力分析的典型用户筛选[J]. 电力系统保护与控制, 2013, 41(11): 146-150.

ZHANG Li-zi, CAI Xue-wen, LU Yu, et al. Peak shifting potential analysis-oriented typical consumers screening[J]. Power System Protection and Control, 2013, 41(11): 146-150.

[9] ANUAR N, ZAKARIA Z. Electricity load profile determination by using fuzzy C-Means and probability neural network[J]. Energy Procedia, 2012, 14: 1861-1869.

[10] ZHOU K, YANG S, SHEN C. A review of electric load classification in smart grid environment[J]. Renewable and Sustainable Energy Reviews, 2013, 24: 103-110.

[11] 王志勇, 曹一家. 电力客户负荷模式分析[J]. 电力系统及其自动化学报, 2007, 19(3): 62-65.

WANG Zhi-yong, CAO Yi-jia. Electric power system load profiles analysis[J]. Proceedings of the CSU-EPSA, 2007, 19(3): 62-65.

[12] 郑晓雨, 马进, 贺仁睦, 等. 基于模型激励响应的负荷分类及泛化能力[J]. 电工技术学报, 2009, 24(2): 132-138.

ZHENG Xiao-yu, MA Jin, HE Ren-mu, et al. Classification and generalization of the load model based on model dynamic responses[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 132-138.

[13] RÄSÄNEN T, VOUKANTSIS D, NISKA H, et al. Data-based method for creating electricity use load profiles using large amount of customer-specific hourly measured electricity use data[J]. Applied Energy, 2010, 87(11): 3538-3545.

[14] 牛东晓, 曹树华, 卢建昌, 等. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 2009.

[15] HAN J, KAMBER M. Data mining: concepts and techniques[M]. Morgan Kaufmann Publisher, 2006.

[16] 李爱国. 数据挖掘原理、算法及应用[M]. 西安: 西安电子科技大学出版社, 2012.

[17] TUNG A K H, XU X, OOI B C. CURLER: finding and visualizing nonlinear correlation clusters[C]. Baltimore, Maryland: ACM, 2005.

Application of clustering analysis in typical power consumption profile analysis

PENG Xian-gang, LAI Jia-wen, CHEN Yi

(1. School of Automation, Guangdong University of Technology, Guangzhou 510006, China; 2. Zhanjiang Power Supply Bureau of Guangdong Power Grid Corporation, Zhanjiang 524005, China)

In order to gain the large power customers’ typical power consumption profiles in a power supply area, a new clustering evaluation method is presented and a clustering analysis framework based on k-means, k-medoids, self-organized maps (SOM) and Fuzzy C-Means (FCM) is built. It analyzes the characteristic of the electricity consumption data and uses the Gaussiansmoothing method to reduce the noise in the data. Clusters average radius, clusters average diameter and clusters average minimum distance are proposed and used to design the clustering evaluation method. This framework is utilized to analyze the daily electricity consumption curves of the whole customers in a certain area, which can automatically recognize the number of clusters. The result shows this methodology is clear in physical conception, simple and practical. This work is supported by Natural Science Foundation of Guangdong Province (No. 10151009001000045).

power consumption profile analysis; Gaussiansmoothing; clustering evaluation; clustering analysis

TM714

A

1674-3415(2014)19-0068-06

2013-12-31；

2014-03-02

彭显刚（1964-），男，副教授，研究方向为电力系统优化运行；E-mail: epxg@gdut.edu.cn

赖家文（1987-），男，硕士研究生，研究方向为电力系统运行分析与控制。

广东省自然科学基金(10151009001000045)；南方电网科技项目(K-GD2012-214)