某型无人水下航行器建模与仿真研究
赵贺伟,宋召青,于华国
(1.海军航空工程学院 山东 烟台 264001;2.92154部队,山东 烟台 264001)
0 引言
无人水下航行器[1](unmanned underwater vehicle UUV)作为未来水下信息战以及重要的反潜扫雷作战平台,越来越受到各国的广泛关注,并有很多国家开展了研究工作。因UUV的实型开发和试验费用昂贵,所以对模型和控制方法的充分研究具有重要的理论与实际意义。本文研究的某型UUV,壳体是流线型,由一个三叶螺旋桨提供动力,由两对水平和垂直舵控制姿态与航向,总长2.17 m,直径0.33 m,排水量0.13 m3,装有多普勒测速仪、方向罗盘、倾角仪和测深仪等与航行控制有关的传感器件。
1 UUV建模
无人水下航行器的建模是研究其控制的基础,建立合适的数学模型关系到整个载体控制系统的优越性,并能够检验控制策略的有效性。
1.1 变量与坐标系的定义[2]
重力——G;偏航角——α;浮力——T;俯仰角——β。
推力——P;滚转角——γ;流体动力——R;潜浮角——θ。
速度矢量——V;航迹角——φ;密度——η;冲角——δ。
侧滑角——ρ;速度滚转角——χ;
航迹坐标系相对固定坐标系角速度——Ω;
载体坐标系相对固定坐标系角速度——ε。
定义4个坐标系:
固定坐标系—dxDyDzD;

载体坐标系—oxOyOzO;

速度坐标系—sxSySzS;

航迹坐标系—hxHyHzH;

文中sinθ=sθ,其他同理。在固定坐标系[3]中,位置矢量w1=[x,y,z]T,姿态角w2=[α,β,γ]T,体坐标系中定义航行器的线速度V=[u,v,r]T,角速度ε=[p,q,l]T,重心位置BG=[xG,yG,zG]T,控制矢量k=[δe(t),δr(t),a(t)]T,δe(t)表示横舵角,δr(t)表示垂直舵角,a(t)表示螺旋桨转速。
1.2 UUV动力学方程的建立
根据动量定理及动量矩定理的相关原理,建立无人水下航行器的动力学方程,由两个矢量方程描述:

1.2.1UUV质心运动的动力学方程

1) 推力在航迹坐标系上的投影[4]。PxH=Pcδcρ;PyH=P(sδcχ+cδsρsχ);PZH=P(sδsχ-cδsρcχ)
2) 重力G与浮力T在航迹坐标系上的投影。将两个力合成一个力GT来讨论。η为载体所在介质的密度,v为载体的体积。则GT的大小为(m-ηV)g。力GT在航迹坐标系上的投影为:
(1)
3) 流体动力在航迹坐标系上的投影及流体动力矩在载体坐标系上的投影[5]。流体动力参数[8]如下:
流体动力及力矩如下:

(2)
(3)
综上所述得到无人水下航行器质心运动动力学方程如下:
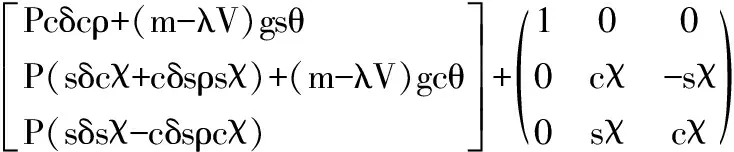
(4)
1.2.2UUV绕质心转动的动力学方程
动量矩可以表示为H=J·ε,其中转动惯量J[6]矩阵形式为:
动量矩H沿载体坐标系各轴的分量为HXO=JXOεXO;HYO=JYOεYO;HZO=JZOεZO
作用在载体上的力矩有重力矩、浮力矩、推力矩和流体动力矩。其中流体动力矩如式3所示,重力矩为MG=0;浮力矩为:

(5)
推力矩为:
(6)
综上所述,可得式(7):
(7)
式(4)和式(7)就是无人水下航行器动力学方程。
2 模型简化
主要做以下模型简化工作:
1) 方程解偶,研究航行器一个平面的运动时令其他平面运动参数为零。将航行器运动解耦为垂直平面的纵向运动,水平面内的侧向运动,以及绕纵轴的横滚运动。
2) 线性化,运用摄动理论,令变量x=x0+Δx,代入解耦方程,再减去原方程,省略Δx,得到线性化方程。
3) 根据控制需要,分成4个控制子系统,即航速、航向、纵倾和深度控制。控制变量见表1。

表1 控制子系统变量
2.1 航速简化模型
(8)
其中:P|a|a和Pua为推进器系数。
2.2 水平面运动简化模型
水平面动力学方程线性模型为:
(9)
2.3 简化后纵平面动力学线性模型
(10)
3 控制器设计与仿真
3.1 航速控制器
由式(8)可知,航速与电机转速是对应关系,选择期望转速ad为控制变量,选择PI控制器,u由声学测速仪测量,控制参数KP=1.28,KI=3.39.仿真结果如图1。

图1 航速控制响应曲线
3.2 航向控制器
根据式(9),对参数v(t),l(t),α(t)进行开环仿真可知,v(t),l(t)开环收敛,而α(t)发散,采用PID控制器进行控制,控制参数分别为KP=5.5,KI=0.01,KD=0.4,可得仿真结果如图2。

图2 航向角α(t)闭环响应曲线
3.3 纵倾角控制器
根据式(9),对r(t),q(t),β(t),z(t)进行开环仿真,可知r(t),q(t)收敛较好,而纵倾角β(t)收敛不好,采用PID控制,控制参数KP=1.2,KI=0.31,KD=0.2,可得仿真结果如图3。
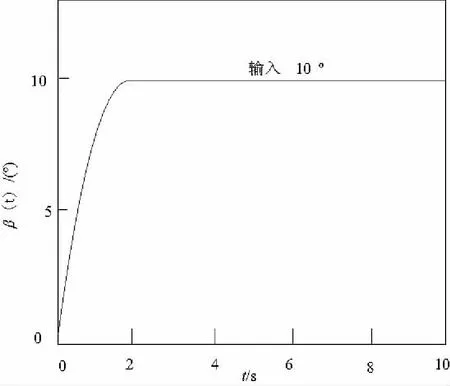
图3 纵倾角β(t)闭环响应曲线
3.4 深度控制器
由开环仿真结果可知深度z(t)发散,可采用PD控制,KP=0.5,KD=0.2,仿真结果如图4。
4 结论
无人水下航行器动力学模型的建立是研究其控制系统的基础,通过小扰动理论和摄动原理将复杂的非线性模型进行简化,由此来设计各子系统的控制器,通过仿真可知,各控制器的设计具有较好的鲁棒性和稳定性,显示了模型建立与简化以及控制器设计的正确性。

图4 深度z(t)闭环响应曲线
[1] 蒋新松,封锡盛,等.水下机器人[M].沈阳:辽宁科学技术出版社,2000:56-59.
[2] 高剑.自主式水下航行器建模与自适应滑模控制[J].西北工业大学学报,2004:39-41.
[3] 肖业伦.飞行动力学的理论基础[M].北京:北京航空航天大学出版社,2003:110-111.
[4] 李天森.鱼雷操纵性[M].北京:国防工业出版社,1999:55-58.
[5] 徐德民.鱼雷自动控制系统[M].西安:西北工业大学出版社,2001:16-27.
[6] Gianluca Antomelli,Stefano Chiaverini,Roboto Finotello,and Riccardo Schiavon Real-Time Path Planning and Obstacle Avoidance for,RAIS:An Autonomous Underwater Vehicle.IEEE Journal of Ocean Engineering,2001,26(2):216-227

