低附带/不敏感炸药作用下战斗部联接强度的计算方法
陈伟,胡有璋,殷春武,王晓鸣,郑宇
(1.中国人民解放军73853部队,江苏 南京 211811;2.南京理工大学 机械工程学院智能弹药国防重点学科实验室, 江苏 南京 210094)
0 引言
炸药反应状态除了受其自身性质、结构尺寸、初始刺激外,温度、压力、气流等外界条件也对其爆炸型式及不同爆炸型式之间相互转化有较大影响。在选定的装药条件下,外界对炸药爆炸型式的影响主要集中在战斗部约束强度,因此准确确定战斗部联接强度的大小对实现战斗部设定功能是十分重要的。
低附带/不敏感和可控战斗部中,常采用螺纹联接限定战斗部的联接强度。螺纹联接强度取决于内外螺纹的剪断过程。其分离是螺纹牙剪切、拉伸、挤压的综合作用过程[1]。在这一过程中除了熟知的由于螺纹牙弯曲产生的挠曲外,还包括剪切力产生的变形,牙根剪切形变产生的变形等。由于紧固条件下螺纹的牙根处除受到拉伸应力的影响外,还受到扭转引起的剪切应力的影响,因此存在最大剪切应力、最大主应力、最大主应变等不同的破坏准则[2]。为达到对战斗部输出威力可调或实现在某种条件下战斗部的顿感和减小附带损伤的目的,需考虑装药在某一爆炸型式的临界破坏压力,因此工程实践中对螺纹副的挤压、剪切、弯曲等强度进行校核,并取1.5~2的安全系数的计算方法或简单通过加长螺纹联接长度的方法不适用该类战斗部设计。此外低附带、不敏感炸药在低速反应过程中不同于抛射药或者发射药燃烧剧烈,其螺纹联接的破坏形态亦不相同。因此,文中对低附带/不敏感炸药作用下螺纹强度计算方法进行推导修正并通过试验加以验证。
1 联接强度的计算方法
在对某低附带/不敏感战斗部进行研究时,通过对回收部件的观察,发现战斗部中螺纹联接破坏情况与紧固件中不同,非薄壁战斗部螺纹牙基本上呈剪切破坏,且未发现明显径向形变,如图1所示。因此,文中近似认为螺纹剪切强度是战斗部中螺纹联接强度。

图1 战斗部分离后螺纹破坏图
首先对单个螺纹副的受力情况进行分析并求出其强度,然后推导螺纹副承载规律,进而得出螺纹副联接强度的计算方法。
1.1 单个螺纹副联接强度的计算方法
螺纹牙根处存在严重的应力集中[3]。在分离的结束状态下螺纹副基本上呈剪切破坏,并且多为内外螺纹中某一个发生剪切破坏,如图2、图3所示。所以在分离过程中,只针对螺纹副的抗剪切强度进行分析。

图2 分离后的外螺纹

图3 分离后的内螺纹
设外、内螺纹的剪切强度极限、剪切面宽度分别为τb1,τb2,hτ1,hτ2,把螺纹牙展开后相当于一根悬臂梁,则按剪切理论[1],如图4所示,得到一个螺距内总的剪切力为:
(1)
在螺纹剪切过程中,剪切面总是沿着抗剪强度最小的方向,因此上述问题即为求解关于hτ1的一元二次方程的最小值,但在计算中要考虑到内、外螺纹的牙顶宽度。通过求解易得螺纹副的最大应力位于牙根处。
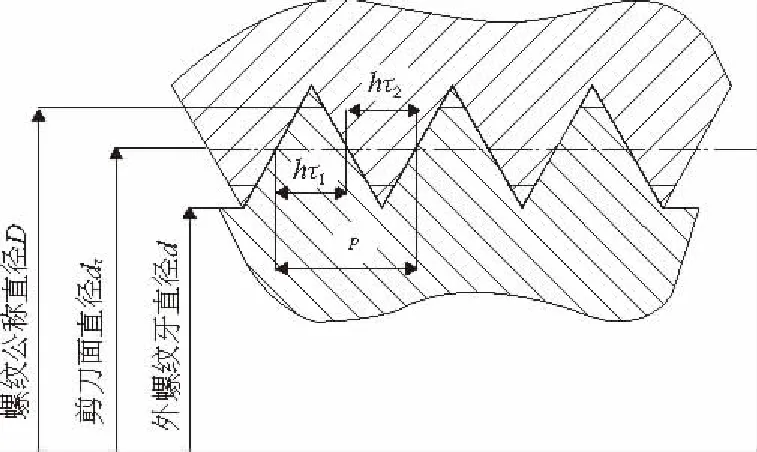
图4 螺纹旋合图示
1.2 螺纹副承载的分布
由于螺纹副之间的载荷并不是均匀分布,内螺纹受压外螺纹受拉的螺纹副中,第一扣载荷最大,且载荷主要集中在前几扣,前三扣载荷占总载荷的60%~70%[4]。因此确定螺纹副承载规律对于计算螺纹副联接强度有着重要意义。
战斗部中内外螺纹受力情况不同于紧固件,其内外螺纹同时受拉。设螺纹副的有效圈数为m,则内螺纹副本体0圈到z圈的伸长是:
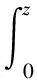
(2)
变形协调条件为:
其中:
ζ/γ=ξ2;ζ=[1/(E1A1)+1/(E2A2)];γ=P2(λ1/E1+λ2/E2)/(πdh);λ1、λ2是无量纲系数,取决于螺纹牙和整个联接的几何参数;E1、E2是外、内螺纹材料的弹性模量;d是中径;h是螺纹牙的工作高度;A1、A2是外、内螺纹本体的横截面积。
对z两次求导,得到:
q″(z)-ξ2q(z)=0
(4)
其边界条件为:
z=0 时,F(0)=0q'(0)=-F/(γE2A2)
z=m时,F(m)=Fq'(m)=F/(γE1A1)
求解得:
(5)
由于q(z)在[1,m]上的图形类似对称轴在[1,m]内开口向上的抛物线,特别地当E1A1=E2A2时,q(0)=q(m)。易得:
q(z)max=max[q(0),q(m)]
(6)
1.3 联接强度
当螺纹副的第1扣或第m扣的螺纹达到其所能够承受的最大剪切应力时,螺纹达到其承载极限值。
即:q(hτ1)min=q(z)max
因此螺纹副的联接强度为:
(7)
2 试验验证
采用长春试验机研究所研制的30T电子万能材料力学试验平台,测试有效旋合圈数为7的不同材质螺纹副(45钢外螺纹分别与45钢、铝、尼龙内螺纹配合)的连接强度。试验装置如图5、图6 所示。

图5 30 T电子万能材料力学试验平台

图6 试件加压
实验采集到的应力-应变数据曲线基本相似,应力随着应变呈波浪形变化并且极值在不断减小,图7为钢-尼龙配合试件载荷-位移曲线。
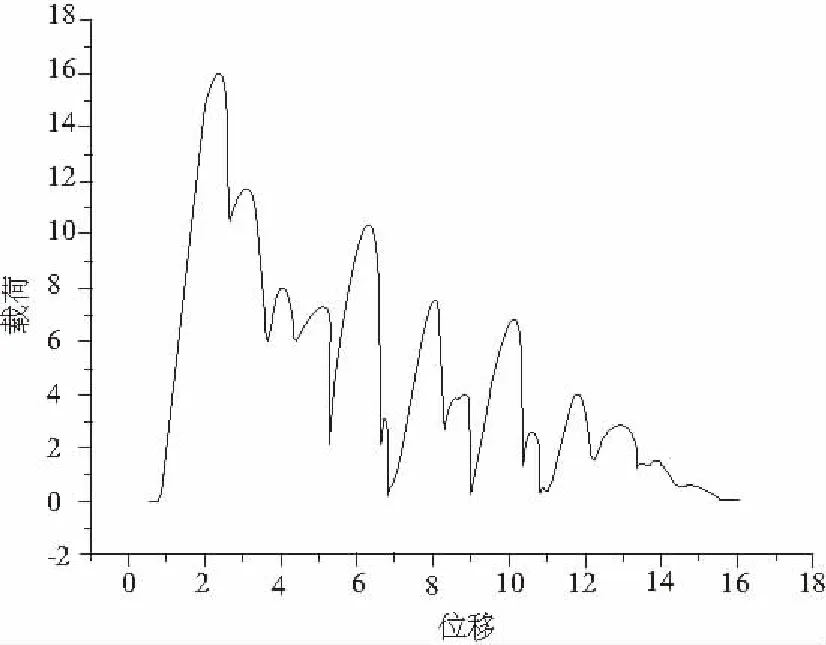
图7 钢-尼龙配合试件载荷-位移曲线
随着载荷的增加,螺纹副的第一扣首先被剪断破坏,此时螺纹副的承载能力达到最大值,随后原螺纹副的第二扣成为新螺纹副的第一扣,直至整个螺纹副被破坏。由于损伤的积累和实际承载螺纹副数量的减少,螺纹副承受的最大载荷将低于原螺纹副的最大载荷。受被剪切螺纹堆积的影响,有个别突越现象,但不影响整个曲线走向趋势和整体规律。
经查表[5], 将刚-尼龙配合试件参数代入式(5)依次求得螺纹副各圈承载百分比q(z)/F分别为:25%,15%,12%,10%,10%,12%,16%。
实验测试强度与公式(7)计算强度对照如表1所示。
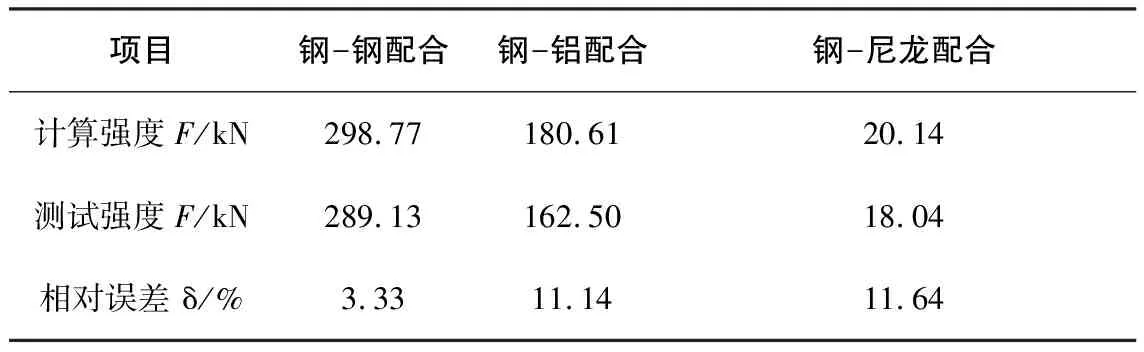
表1 螺纹副计算强度与测试强度对比表
对比计算强度和测试强度可知,公式(7)计算结果能够较好的反映出螺纹联接强度。
3 结语
通过实验观察,战斗部中螺纹联接在低附带/不敏感炸药作用下,基本呈剪切破坏且是内、外螺纹中某一个发生破坏。对单个螺纹扣剪切受力分析,得出了螺纹扣的受力公式,并解释了螺纹牙根处发生剪切的现象。对内外同时受拉螺纹副承载规律进行总结和推导,提出了在低附带/不敏感炸药作用下战斗部联接强度的计算方法。经试验验证,该计算方法能够较为准确的计算出低附带/不敏感炸药作用下战斗部联接强度。
[1] 刘文举.抛射起动压力的计算方法[J].弹箭与制导学报,2008,28(4):102-104 .
[2] 山本晃.螺纹联接的理论与计算[M].郭可谦,等译.上海:上海科学技术文献出版社,1984.
[3] CHAABAN A, JUTRAS M.Static analysis of buttress threads using the finite element method[J].Journal of Pressure Vessel Technology, 1990, 114: 209-212.
[4] 陈海平,曾攀,方刚,等.螺纹副承载的分布规律[J].机械工程学报,2010,46(9):171-178.
[5] 卜 炎.螺纹联接设计与计算[M].北京:高等教育出版社,1995.

