壅水条件下推移质泥沙输沙率变化规律初步研究

，

(1.长江科学院 河流研究所，武汉 430010；2.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

现有推移质输沙率公式一般都基于恒定均匀流水槽试验资料和近似均匀流天然河流观测资料得出来的，而壅水条件下(非均匀流，属减速流)，特别是河道型水库，相同流量下从库尾至坝前水深逐渐增加，其非均匀性逐渐加大的情况下，此类推移质输沙率计算公式是不适用的。非均匀流的水流结构与均匀流有明显的不同，非均匀性愈强差别也愈大，沿用均匀流的推移质输沙率研究成果来分析研究非均匀性较强的问题，往往会产生较大的偏差。

关于非均匀流(尤其是壅水条件下减速流)的推移质泥沙输移的研究相对较少。Hoan[1]通过沿程增大水槽宽度形成减速流，试验研究水流强度参数与卵石输沙强度参数的关系，发现shields水流强度参数Ψ与输沙强度参数Φ相关系数只有0.18，而引入紊动强度参数后其相关系数达到0.77以上，并指出计算非均匀流条件下卵石起动条件时必须考虑近床面紊动强度。卢金友[2]发现：在峡谷壅水河段，水流切应力、水流功率和流速指标都不能较好地预测输沙强度。Afzalimhr[3]研究了减速流下砂砾石床面泥沙的起动，发现在减速流下其切应力沿水深成凸型分布，且临界shields数较均匀流条件下要小。临界shields与相对水深没有明显的相关关系。Khorram[4]通过敏感性分析选定与库区推移质运动相关的几个关键参数，利用人工神经网络方法得到适用于沙、砾石、混合沙的输沙关系式。壅水条件下水流结构特征及推移质泥沙输移规律问题尚未得到很好的揭示和解决，如天然壅水河段、水库库区壅水等条件下的泥沙输移、河床冲淤等问题，亟需这方面的理论支撑。因此，开展壅水条件下非均匀流的运动特性及推移质输移规律的研究，对于泥沙运动力学及河床演变学的发展具有重要的理论意义及实用价值。

2 壅水条件下现有推移质输沙率公式的检验

为了阐述壅水条件下推移质泥沙输沙率的变化情况及公式的检验效果，现以万县站为例来进行分析。

万县站位于三峡水库常年回水区，距坝址约300 km。天然情况下，该河段水深为12～30 m，河宽在400～600 m之间，水面比降约为0.9；坝前按135 m运用时，汛期同流量下水深抬高约15～25 m，河宽在685～715 m之间，水面宽度比天然情况增加100 m左右，水面比降0.1～0.2，流速相应减小1 m/s左右；坝前按145 m运用时，汛期同流量下水深抬高约25～35 m，河宽在705～785 m之间，水面宽度比天然情况增加100～185 m左右，水面比降0.07～0.09，流速相应减小1.5 m/s左右。万县站不同阶段水位流量关系见图1；万县站不同阶段水面比降和流量关系见图2。

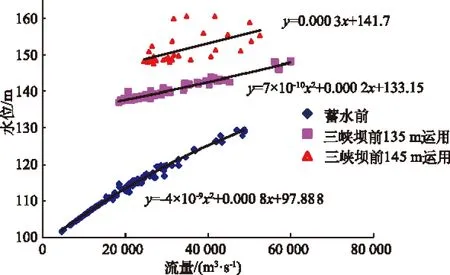
图1 万县站不同阶段水位流量关系

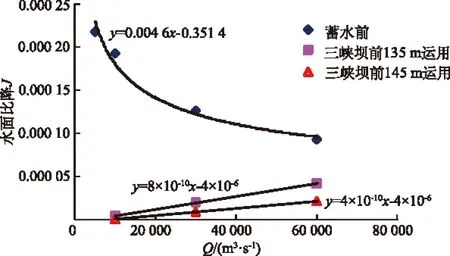
图2 万县站不同阶段水面比降和流量关系

通过点绘万县站天然条件下、三峡水库坝前135 m运用条件下和145 m运用条件下的水流参数Ψ和输沙强度Φ的关系及与6家公式曲线的对比分析(见图3)，可知：万县站整体输沙强度都比较小，随着壅水程度的加剧，万县站输沙强度呈减小趋势，壅水条件下万县站的总体输沙强度比天然时要低，其中145 m运用条件下更低；关于水流参数Ψ和输沙强度Φ的关系，三峡水库蓄水前天然条件下6家公式基本能描述其关系，但坝前135 m运用条件下和145 m运用条件下Ψ和Φ的关系与6家公式有偏离趋势，而且随着壅水程度的增加，其偏离程度亦呈增加趋势。经统计，坝前145 m运用条件下需要较蓄水前增加5倍的水流强度才能输送相同输沙强度的推移质，即随着壅水程度的增加，水流参数Ψ和输沙强度Φ的关系与6家公式偏离程度也增加。

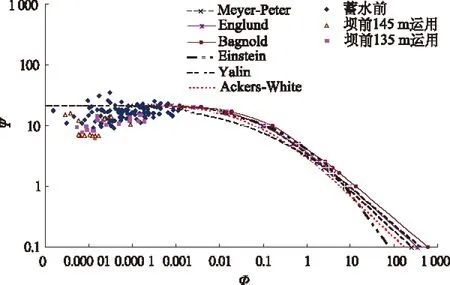
图3 万县站不同水位条件下实测资料与各家公式的对比

由上述可知，6家经典推移质输沙率公式并不能用来预测壅水条件下的推移质输沙率，而且随着壅水程度的增加其准确性越来越差。

3 不同壅水条件下水流结构水槽试验

为了对壅水条件下推移质的输运进行研究，先考虑不同壅水条件下水流结构的变化。通过对比不同壅水条件下水流结构与均匀流条件下水流结构的差异，分析得到影响壅水条件推移质输沙率的因素，进而对现有的推移质输沙率公式进行修正。关于壅水条件暨考虑壅水高度的影响下水流结构与非均匀流的差异，以前也有学者提到，但是关于这方面的研究极少。为此，进行不同壅水条件下清水水槽试验，分析不同壅水条件下水流结构及切应力的变化。

3.1 试验设计

试验采用水槽全长24 m、宽0.6 m、高1 m，水槽底部用水泥抹面，两侧壁为玻璃。试验水槽设备由水流循环系统、流量调节系统、水深控制系统及辅助设备组成。水流循环系统由水泵、输水管路、试验水槽及其蓄水水库组成的封闭自循环系统；由水泵从蓄水水库提水进入输水管路，然后注入量水池，流过量水堰，经试验水槽又流回蓄水水库；水槽前部加设栏栅已平稳水流，水槽尾部设置闸门控制水深。流速采用声学多普勒测速仪(ADV)测量。

试验采用2级流量，每级流量下测量不同控制水深的水流流速分布，同时测量水面比降。水槽坡度取为1.5‰，通过尾门控制测量断面水深。为了消除尾门和进口处水流波动的影响，测量断面选择水槽中间部位。每个断面布置5条垂线，根据需要垂线上布点由上往下加密。为了观察底部变化，每条垂线近底5 cm加密，用ADV测量垂线上各点的流速，每个点的测量时间为4 min。

试验测量40 L/s流量级5组水深，70 L/s流量级4组水深，共测9组。每个流量级中有1组为均匀流，其余组次控制流量不变壅高水位，以研究壅水条件和正常水深条件下的水流结构等差别。试验中控制水深时，固定控制断面，每级流量的水深以该断面进行控制。水槽试验参数见表1。

表1 水槽试验参数

本试验主要研究壅水程度对水流结构的影响，所以可取壅水水深与正常水深的比值作为该水流条件壅水程度指标,即

(1)

式中：β为壅水程度指标；h0为正常水深高度，即壅水高度为Δh=h-h0。

3.2 试验结果分析

3.2.1 流速沿垂线分布

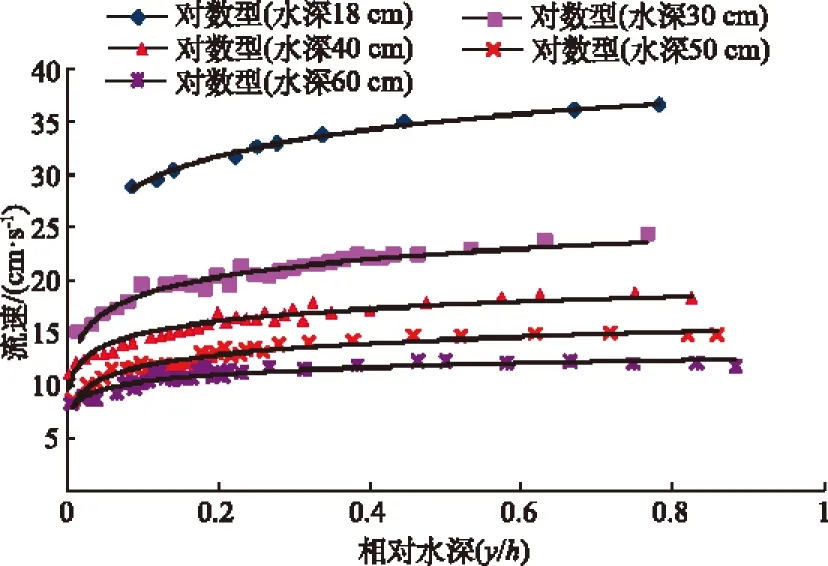
(a) A组

(b) B组

不同研究者对均匀流的流速分布进行了深入的研究，也取得了较为丰富的成果。归纳起来有以下几种形式：对数型、指数型、抛物线型、椭圆型、反双曲正切型等。其中应用最为广泛的是对数型分布公式和指数型分布公式。图4分别为2个流量级下不同水深的纵向流速沿垂线分布。

从图中可以看出，流速分布大致符合对数率，但是还是存在一定差别。在距离底面相对位置0.2以上流速与对数率有分离现象，尤其在靠近水面附近。近些年来的研究表明，水面附近流速分布于对数率分离主要是由二次流产生的。Yang[11]指出，由于垂向流速不为零，它将和壁面剪切运动产生一个额外的动量，影响纵向流速分布。

现有研究发现，明渠的均匀流和非均匀流均存在分区结构，分为内区和外区。内区(00.2)的时均流速分布有不同的观点，因二次流对流速分布的影响还为有突破性的进展，即使对于均匀流外区流速分布也存在争议。由于本试验主要分析与推移质输沙关系密切区域的水流结构，因而对于外区的流速分布暂不考虑。利用实测数据经拟合得到近底区流速分布为

(2)

分析得出：壅水条件下水流流速沿垂线分布较均匀流条件下更加均匀，当壅水程度越大(β越大)时，水流流速沿垂线分布越均匀，即流速梯度越小。

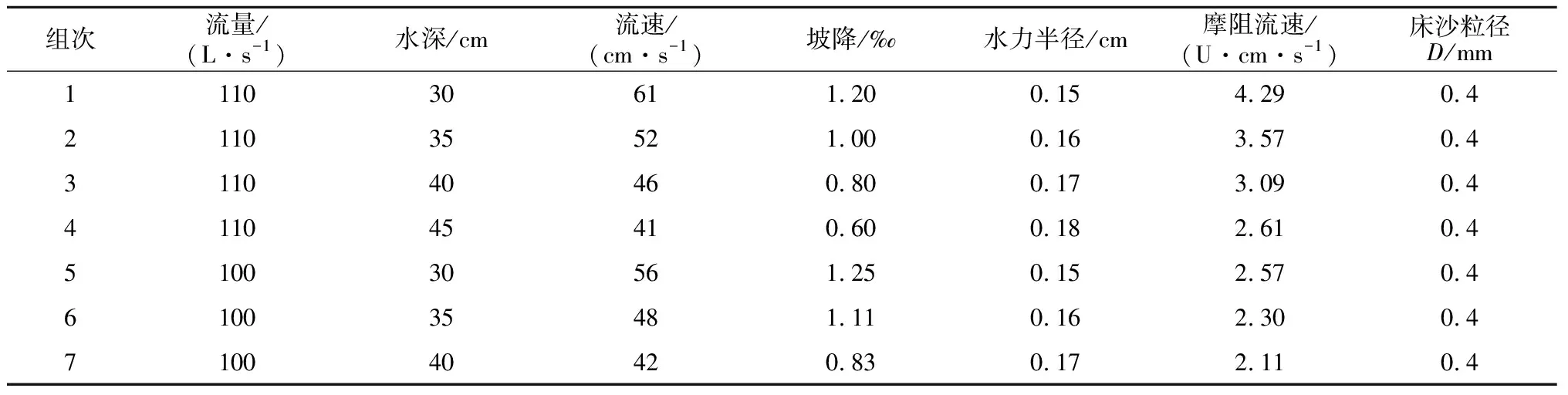
表3 推移质输沙率水槽试验条件

3.2.2 床面切应力的变化规律

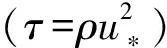
(3)

表2 τ/τ0随β的变化统计

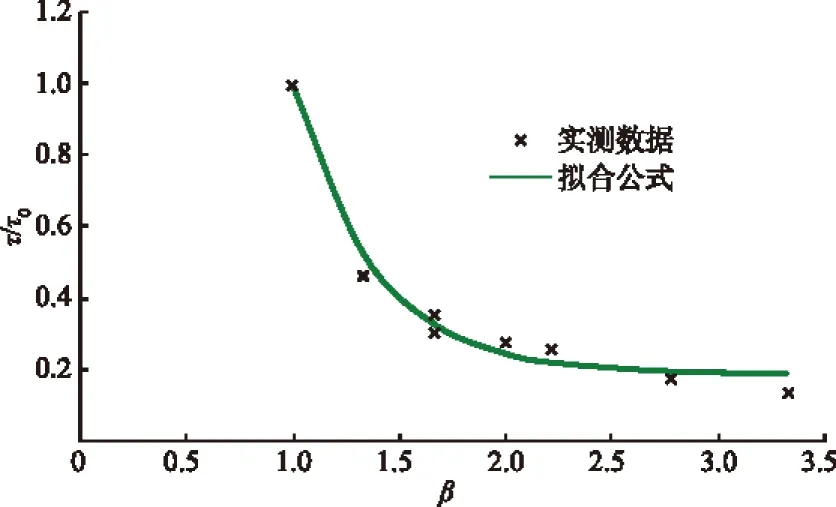
图5 τ/τ0与β的关系拟合图

可以看出，随着壅水高度的增加，相对切应力τ/τ0的变化率不断减小。当β(=h/h0)达到1.5，即壅水高度达到正常水深的50%时，其床面切应力减小到均匀流状态的40%，β在1～1.5范围内，床面切应力减小幅度最大。随着β的增加，床面切应力的衰减幅度不断减小，当β达到2时，其床面切应力为均匀流状态的25%，此后床面切应力开始趋于稳定。

4 壅水条件下推移质输沙规律

4.1 不同水深条件下试验输沙率比较

本试验在水清试验的基础上，开展壅水条件下推移质输沙水槽试验。主要观测项目是水深、比降、流速分布、紊动及推移质输沙率，共进行了2级流量下7个组次试验。每级流量时，先进行恒定均匀流输沙试验，即正常水深条件下的平衡输沙率。然后在此基础上抬高水位，试验测得控制断面处不同壅水条件下的输沙率。为了简化说明问题，阐述规律，采用均匀沙进行试验，本次试验采用粒径为0.4 mm的天然沙。每组试验条件见表3。

为了观测推移质输移特性和检验推移质输沙率公式，利用实验室水槽进行均匀沙输沙率试验，现进行正常水深条件下平衡输沙试验，表3中第1和第5两个组次进行平衡输沙试验。试验过程中第1次试验放清水，清水冲刷试验直至床面运动泥沙很少或按初始可动沙平均粒径进行计算的输沙强度参数大致小于0.001时，即可停止试验。在水槽尾部测推移质输沙率，本次试验的实测输沙率用于第2次试验时的加沙组成，第3次试验用第2次的实测值加沙组成。如此重复操作，可得到各组次加沙率和接沙率基本相同的平衡输沙过程，从而确定各组次的平衡输沙率。测出输沙率和水深、流量、流速分布、比降等因子。

在壅水条件下，先选定并固定控制断面，非均匀流的水深就以该断面进行控制，接沙输沙率的测量也以该断面为准。为了保证床面的一致性，进行壅水条件下输沙试验时，上游不加沙以预防淤积三角洲的产生，并预留足够长的上游试验段保证床面推移质的输移；而且，在控制水位调到预定值后，即开始计时接沙，接沙历时为0.5～1 h即结束，以此测定该控制水位下的输沙率。

根据预定的方案共进行了7个组次推移质输沙率试验，试验中主要对流量、控制断面的流速分布、水深、水面比降、推移质取样时间及输沙量等因素进行了测量，得出各组次该控制断面的单宽输沙率，并按各组次水沙条件，采用Einstein，长江科学院曲线，Yalin，Engelund，Bagnold，Parker，Meyer-Peter and Muller(简称MPM)公式计算各组次输沙率，各组次单宽输沙率的计算值和实测值的比值(gb计算/gb实测)与壅水程度指标β的关系见表4。由表4可见，各家公式在壅水条件下计算的单宽输沙率偏大，而且随着壅水程度指标β的增加，gb计算/gb实测的值越来越大，如当β达到1.33～1.5时，平均gb计算/gb实 测的值达到了18.2～21.3，即使考虑正常水深下公式本身和实测值的偏离，当β达到1.33～1.5时，平均gb计算/gb实测值还是明显偏大很多倍。可见，当壅水程度指标β达到1.3以上时，前述各家公式已不适合用来计算推移质输沙率。

表4 gb计算/gb实测与β的关系

点汇本次壅水条件下水槽试验资料水流参数Ψ和输沙强度Φ之间的关系，结合刘兴年[14]和 Wilson[15]推移质平衡输沙水槽试验资料，并选取Meyer-Peter，Englund，Bagnold，Einstein，Ackers-White，Yalin6家典型公式进行比较，见图6。同样说明，平衡条件下实验数据和各家公式基本吻合，但壅水条件下偏差较大，而且随着壅水程度的增加，偏离越来越大。

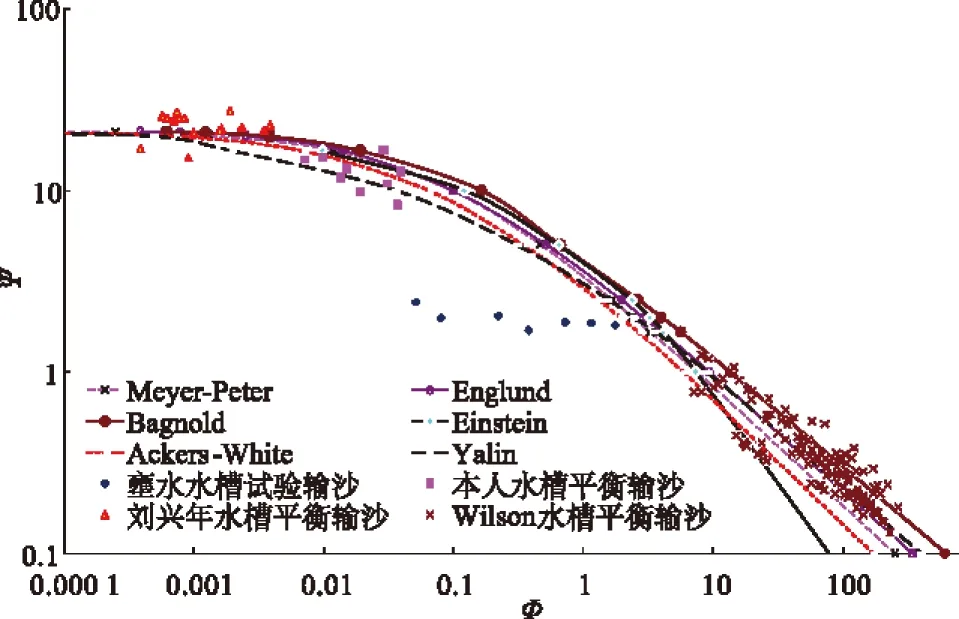
图6 不同条件下水流参数和输沙强度的关系对比

4.2 壅水条件下推移质输沙率公式初探

水流泥沙运动是典型的两相流运动，影响输沙率大小的主要是水流因数(液相)和泥沙因数(固相)。水流因数包括：水深h、坡降J、流速U、重力加速度g、密度ρ、运动黏滞系数υ；泥沙因数包括：粒径D、沉速ω、密度ρs，因此泥沙输沙率gb=f(h,τ0,u,g,ρ,υ,d,(ρs-ρ)/ρ)。而输沙公式的本质在于建立单宽重量输沙率gt与水流强度指标T之间的关系。一般均采用指数形式的函数，即

gt=aTb。

(4)

式中a为系数；b为指数。由于水流强度指标与输沙率的量纲不尽相同，因此需将他们无因次化。

通过对现有输沙率公式的分析，水流强度指标最终由3项组成:1是平均流速;2是坡降;3是水深[16]。因此可以以统一的形式表示为

T=kha1ua2Ja3。

(5)

式中:k为系数，仅与水流和泥沙的性质有关;a1，a2，a3为指数。

考虑将水流切应力指标作为预测推移质泥沙输移强度的指标[17]。壅水条件下的推移质输移规律更加复杂，对于壅水条件下的推移质输沙率公式，引入壅水程度指标β。通过无因次化，从而可得无因次形式的水流强度指标形式为

(6)

式中c1，c2，c3，c4，c5为常数。

输沙强度指标采用Einstein无因次输沙强度Φ，即

利用前述万县水文站的天然河道实测资料、坝前135 m运用、坝前145 m运用及水槽试验资料对上述通用输沙率公式进行率定，得出适合长江上游河段，特别是三峡库区河段的推移质输沙率公式，见公式(7)。

(7)

利用回归分析以确定通用公式中的各指数及系数。其回归精度见图7。考虑到回归样本的局限性，推荐在水库库区壅水河道特别是三峡库区河段使用本文回归公式。

图7 式(7)的回归精度

5 结 论

(1) 根据实测资料分析，指出了现有经典推移质输沙率计算公式在壅水条件下的不适用性。并结合水槽试验得出：壅水条件下现有公式计算的单宽输沙率偏大，而且随着壅水程度指标β(即壅水条件下水深和正常水深的比值)的增加，gb计算/gb实测的值越大。当β达到1.3以上时，现有各家公式已基本不能用来计算壅水条件下的推移质输沙率。

(2) 研究了壅水条件下的水流结构特征，并得到了相对床面切应力与壅水程度指标β的定量关系。通过不同壅水条件下清水水槽试验，分析发现：床面切应力随壅水程度的增加而减小。并得到了τ/τ0与β的变化关系式，定量分析了τ/τ0随β的变化趋势。

(3) 引入壅水程度指标β，将水流强度和输沙强度指标无因次化，结合天然实测资料和水槽试验资料，回归分析得出了适合在水库库区壅水河道的推移质输沙率计算公式。

参考文献：

[1] HOAN N T. Stone Stability under Non-uniform Flow[D]. Delft: Delft University of Technology, 2011.

[2] 卢金友，金中武,郭 炜,等. 长江上游推移质泥沙输移研究[J].长江科学院院报，2009,26(1)：5-8.(LU Jin-you，JIN Zhong-wu, GUO Wei,etal. Study on Bed-load Sediment Transport in Upstream of Yangtze River[J].Journal of Yangtze River Scientific Research Institute，2009, 26(1)：5-8. (in Chinese))

[3] AFZALIMHR H, DEY S, RASOULIANFAR P. Influence of Decelerating Flow on Incipient Motion of a Gravel-bed Stream[J]. Sadhana, 2007, 32(5): 545-559.

[4] KHORRAM S, ERGIL M. Pinpointing the Key Parameters in Estimating the Bed-load Sediment Flux in Reservoir Engineering[M]. Environment Earth Science, 2011, 66(7): 2109-2127.

[5] MEYER-PETER E, MULLER R. Formulas for Bedload Transport[C]∥IAHR. Proceedings of the 2nd Meeting of the International Association of Hydraulic Research, Stockholm, June 7, 1948：39-64.

[6] ENGELUND, F, HANSEN E. A Monograph on Sediment Transport in Alluvial Streams[M]. Denmark: Teknisk Vorlag, 1967.

[7] BAGNOLD R A. An Empirical Correlation of Bedload Transport Rates in Flumes and Natural Rivers[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1980, 372(1751): 453-473.

[8] EINSTEIN H A. Formulae for the Transportation of Bed-load[J]. Transactions of ASCE, 1942，107：561-577.

[9] ACKERS P, WHITE W P. Sediment Transport: New Approach and Analysis[J]. Journal of Hydraulic Division of American Society of Civil Engineering, 1973，99(HY11)：2041-2060.

[10] YALIN M S. An Expression for Bedload Transportation[J]. Journal of Hydraulic Division of American Society of Civil Engineering, 1963，89(HY3)：221-250.

[11] YANG S Q, XU W L, YU G L. Velocity Distribution in a Gradually Accelerating Flow[J]. Advances in Water Resource, 2006, 29(12): 1969-1980.

[12] KIRONOTO B, GRAF W H. Turbulence Characteristics in Rough Non-uniform Open-channel Flow[J]. Proceedings of the ICE: Water Maritime and Energy, 1995, 112(4):316-348.

[13] 申红彬. 顺直及微弯型河流水流阻力分析[D].武汉:武汉大学, 2011. (SHEN Hong-bin. Flow Resistance of Straight and Slightly Sinuous Rivers[D]. Wuhan: Wuhan University, 2011. (in Chinese))

[14] 刘兴年，非均匀沙推移质输沙率及粗化稳定[D].成都：成都科技大学，1986. (LIU Xing-nian. Transport Rate and Coarsening Stability of Non-uniform Bedload[D]. Chengdu: Chengdu University of Science & Technology, 1986. (in Chinese))

[15] NNSDI F N, WILSON K. Motion of Contact-load Particles at High Shear Stress[J]. Journal of Hydraulic Engineering, 1992, 118(11): 1670-1684.

[16] 黄才安，杨志达.泥沙输移与水流强度指标[J].水力学报，2003，(6)：1-7. (HUANG Cai-an, YANG Zhi-da. Sediment Transport and Flow Intensity Indexes[J]. Journal of Hydraulic Engineering, 2003，(6)：1-7. (in Chinese))

[17] 金中武.壅水条件下推移质泥沙输移规律初步研究[D].武汉：武汉大学，2012. (JIN Zhong-wu. Preliminary Study on Bedload Transport under Backwater Flow [D]. Wuhan: Wuhan University, 2012. (in Chinese))