基于三元数的复平面J集构造研究

阚淋琳 ，王化雨

（1.山东师范大学 信息科学与工程学院，山东 济南 250014；2.山东省分布式计算机软件新技术重点实验室，山东 济南 250014）

自1980年首次被计算机绘出来之后，J集[1]以其独特精妙的复杂结构引起了科学工作者广泛深入的研究。目前二维J集画法和性质的研究[2]都是基于二元数（复数），三维J集分形图都是基于三元数、四元数等超复数。本文在传统三元数定义的基础上，对三元数虚轴单元的运算关系进行了探究，基于不同运算关系的虚轴单元的三元数来构造二维J集。用三元数构造二维J集时，由于比二元数多了一个自由的数值，用它来对图形进行色彩、形状等某方面的控制，得到的图形就会比二元数构造的J集分形图携带更多的信息，呈现出更多的特色。

传统J集绘制在色彩方案的选择上只能借助于外在的参数，比如利用逃逸时间算法[3]中涉及的逃逸半径、逃逸迭代次数，或依据以上两种因素引入色彩控制球[4]或调色板[5]等技术。本文利用第3个虚轴单元的系数来达到控制颜色的目的，与以往的渲染方案相比，得到的部分彩色图像甚至有了伪3D的效果。

1 三元数

1.1 三元数定义

一般意义下，复数 Zn形如 x+yi，也就是具有 1个虚部和1个实部的复数，或者说是具有1个虚数单位的复数。但事实上，复数也可有多个虚数单位。

所谓超复数[6]是对复数系的虚部进行各种扩展而得到的，它的基本形式是虚部的个数大于1，可定义为：

其中，n=1，2，…；a 和 an是实数；in是虚数单位。

可以看出，超复数有1个实部、多个虚部。在研究、表达时，常根据超复数是由几部分组成的而称其为“某元数”。

超复数的基本形式为z=a0+a1i1+a2i2+…+anin，若要得到2-D（i，j）截面，映射的方法为第 i个虚轴单元的实数部ai对应直角坐标系的x轴，第j个虚轴单元的实数部aj对应直角坐标系的 y轴。 若要得到 3-D（i，j，k）截面，只需在 2-D（i，j）截面坐标关系对应的基础上，让第 k个虚轴单元的实数部ak对应直角坐标系的z轴。这样，所谓三元数就是具有1个实部和2个虚部的超复数，如此，三元数的形式为 T=a+bi+cj，其中 a、b、c 为实数，i、j为虚数单位。三元数的映射方法为：a对应空间坐标系中的x轴，b对应坐标系中的y轴，c对应坐标系中的z轴。

1.2 自定义三元数

区别于三元数定义，本文将三元数定义为T=ai+bj+ck，其中 a、b、c 为实数，i、j、k 为 3 个虚数单位。 三元数T=a+bi+cj即为当i2=1时的特殊情况。当3个虚轴单元有不同的定义时，可得到不同性质的三元数。

（1）一般三元数：i2=i，j2=k，k2=-j，i×j=j×i=j，i×k=k×i=k，j×k=k×j=-i。 根据这种运算关系，三元数 T1和 T2分别相加、相减、相乘可得：

此类运算关系是根据超复数[7]定义，对 n个虚轴单元的关系由一般到特殊转化为三元数而得来的。此类三元数具有以下性质：

①加法满足交换律和结合律。

近年来颅脑MR用于诊断FES。通常患者神经系统症状出现4 h后T2WI显示异常信号改变。弥散加权MRI图像显示：出现特征性“星－场”模式的，同时出现细胞毒性水肿（急性期：1～4 d）。在脑室周围白质和皮质下区域的双边白质异常（亚急性期：5～14 d）。多发性点状损害,提示有脂肪小球阻塞毛细血管［7］。但临床上获得的颅脑MRI一般为亚急性期，急性期因患者意识障碍、烦躁或生命体征不稳定，无法完成MRI检查。

②乘法满足交换律、结合律和分配律。

（2）复数化三元数：j2=k2=-1，i=1，i×j=j×i=j，i×k=k×i=k，j×k=k，k×j=-k。根据这种运算关系，三元数 T1和 T2分别相加、相减、相乘可得：

此类运算关系是根据哈密顿四元数中各个虚轴单元之间的运算关系得来的。此类三元数的重要性质不满足乘法交换律。例如方程x2+1=0，把三元数带进去之后变为（ai+bj+ck）2+1=0，满足此关系式的解有无数个，该方程就有无数个根，因此此类三元数具有解的不定特征。

（3）超三元数：i2=j2=-1，k2=1，i×j=j×i=k，i×k=k×i=-j，j×k=k×j=-i。 根据这种运算关系，三元数 T1和 T2分别相加、相减、相乘可得：

此种运算关系是根据可交换超复数中各个虚轴单元之间的运算关系得来的。由上可得，此类三元数与一般三元数具有相同的性质，不同的是，超三元数经过乘法运算后得到的是一个四元数。

2 色彩方案

J集最典型的着色技术[8]是基于逃逸时间算法的，一种是根据迭代次数k进行着色，另一种是根据“距离”r进行着色。本文采用的着色技术亦是基于逃逸时间算法，但是利用了三元数的特殊性。

根据三元数的定义T=ai+bj+ck，映射方法为a对应直角坐标系中的 x轴，b对应坐标系中的y轴，c即可用来控制颜色。a、b的值可由绘制区域的设定而得到。c的初始取值可以由用户自行设定，设定分为两个方面：一是取值不存在任何几何意义，可自由设定任意实数值；二是根据点的坐标来设定，如可以设定为迭代点到原点的距离、迭代点的横坐标和迭代点的纵坐标等，不同的设定即可得到不同的分形图。

3 J集生成过程

J集是具有无线细分的自相似层次结构的图形，但是计算机却是基于离散像素显示的，因此只能在一定范围内近似表示。J集的生成过程如下。

（1）复动力系统 zn+1=zn2+c（n=0，1，2，…），c 的取值非常灵活，可以是实数、复数或三元数，这里因研究需要，将c设定为复数。

（2）划定三元数初始值范围空间，把第一、二维虚轴单元的系数分别对应 x、y轴，它们的取值范围是⎿xmin，xmax」、⎿ymin，ymax」，并设定相应区间的步长间隔为 △x、△y。

（3）令 Nx=（xmax-xmin）/△x，Ny=（ymax-ymin）/△y，在整个迭代区间建立网格，每个子网格大小为 △x×△y，因此，整体子网格数为 Nx×Ny，而三元数J集的计算最终归结为计算网格点是否属于J集。

（4）设置最大迭代次数M以及逃逸半径R。

（5）令 x0=xmin+nx×△x，y0=ymin+ny×△y。

（6）针对不同虚轴单元的运算关系，迭代过程计算也不同，由（xt，yt）算出（xt+1，yt+1），计数 t=t+1。

①xt+1=x2-2×y×z，yt+1=2×x×y-z×z，zt+1=2×x×z+y×y。

②xt+1=x2-y2-z2，yt+1=2×x×y，zt+1=2×y×z。

③实数部分为-x2-y2+z2，xt+1=-2×y×z，yt+1=-2×x×z，zt+1=2×x×y。

（7）计算 r=x2+y2：

①如果 r＞R，则选择颜色 t，转至步骤（8）。

②如果 r=R，则选择颜色 0（黑色），转至步骤（8）。

③如果 r≤R且 t＜M 则转至步骤（6）。

（8）对点 nx、ny着颜色 t并转至下一点，再转回步骤（5）。

4 实验验证

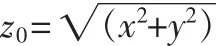
图1 一般化三元数z0=x0

图2 复数化三元数z0=x0

本文通过复动力系统 zn+1=zn2+c（n=0，1，2，…）中 z的取值从实数到三元数的改变，绘制出复平面J集。并对不同种类的三元数性质进行分析，利用逃逸时间算法，结合三元数中第3个虚轴单元最后迭代结果来控制颜色。实验结果表明，本文提出的基于三元数绘制J集的方法可行。但是，本文的计算过程中各个参数的取值及J集是提前设定的，具有一定的局限性，在用户交互自由选择方面仍需进一步地研究。

[1]文志英，井竹君.分形几何和分维数简介[J].数学的实践与认识，1995（4）：20-34.

[2]BARNSLEY M F.Fractals everywhere[M].New York：Academic Press，1988.

[3]FALCONER K.分形几何——数学基础及其应用[M].曾文曲，等，译.沈阳：东北大学出版社，1994.

[4]CARLSON P W.Two artistic orbit trap rendering methods for Newton M-Set fractals[J].Computer&Graphics， 1999，23：925-931.

[5]叶瑞松.Newton迭代及其生成的3D分形图像[J].计算机工程，2001：27（10）：144-145.

[6]KANTOR IL， SSOLODOVNIKOV S.Hypercomplex number：an elementaryintroduction to Algebras[M].New York： SpringerVerlag， 1989.

[7]屈鹏展.n元数及其性质[J].宝鸡师范学院学报（自然科学版）.1993（1）：107-123.

[8]张敏，王化雨.广义M_J集自动配色方案的研究与应用[J].计算机技术与发展，2010：20（3）：59-62.