一种改进RANSAC的基础矩阵估计方法

甄 艳，刘学军，王美珍

(1. 南京师范大学 地理科学学院，江苏 南京 210023；2. 南京师范大学 虚拟地理环境教育部重点实验室，江苏 南京 210023)

一、引 言

从不同视点处获得同一场景的两幅图像间存在重要的几何约束关系，即对极几何关系。对极几何独立于场景结构，是在非标定情况下可以从图像中获得的唯一信息。基础矩阵是对极几何关系的代数表示，它的准确求解是解决其他视觉问题的关键环节之一，如三维重建[1]、运动估计、相机自标定[2]、匹配及跟踪的基础。目前，利用图像间对应点来估算基础矩阵的方法主要可以分为3类：线性方法、迭代方法和鲁棒方法[3]。线性方法的特点是计算速度快，但对于噪声和错误匹配非常敏感；迭代方法的精度通常比线性方法高，但计算时间长。当匹配点集中出现错误匹配时，线性方法和迭代方法已经不再适用，而鲁棒方法可以解决这类问题，如最小中值法(least median squares，LMedS)、随机抽样一致性法(random sample consensus，RANSAC)及M估计算法(M-estimator sample consensus，M-Estimators)，这类方法的特点是对噪声和错误匹配都有更好的鲁棒性。当错误数据超过50%时，RANSAC仍能获得较好的结果，近年来根据RANSAC算法的思想衍生出MINPRAN算法[4]和MLESAC[5]等算法。

传统RANSAC算法在外点比率较大时算法效率较低，Matas和Chum[6]提出的预检验算法可有效提高算法效率，陈付幸[7]和田文[8]等在此基础上重新设定预检验的条件，设计了自适应的预检验方法。RANSAC算法也存在样本选择的随机性导致结果具有较大随机性的问题，刘坤[9]和鲁珊[10]等提出基于概率抽样的方法来解决这一问题，该方法可在一定程度上提高算法的精度，但由于在模型检验过程中需要计算每个样本点的抽样概率并根据设定的阈值来选择样本点，计算过程较复杂。针对上述问题，本文提出了一种改进RANSAC的基础矩阵估计算法。

二、RANSAC算法效率与精度分析

RANSAC算法的基本思想是在保证一定置信概率的前提下，经过多次抽样取得至少一个样本包括的点全是无污染的样本，从而保证得到正确的参数模型。其计算过程实质上可看做是模型的假设与验证的过程，如图1所示。在模型假设阶段，从原始数据中随机抽取最小子集来估计模型参数；在模型验证阶段，需要对估计的模型参数进行验证，验证方法一般是计算原始数据中与估计的模型参数相容的样本数量。

1. RANSAC算法效率分析

设原始数据中共有N对匹配点，从中随机抽取一个最小子集来估计模型参数的时间，记为Cestimate，用一个数据检验模型参数需要的时间，记为Cfitting，则用原始数据中的全部数据检验模型参数的算法复杂度为O(NCfitting)。因此，RANSAC算法完成K次样本假设与验证的过程算法复杂度为

图1 RANSAC算法流程图

(1)

从式(1)可以看出，影响RANSAC算法计算效率的因素主要有两个：抽样次数和模型验证所需时间。因此，要提高RANSAC算法的效率，可减少抽样次数和减少模型验证所需的时间。

2. RANSAC算法精度分析

由于在特征点提取与匹配过程中不可避免会含有噪声和外点数据，在外点比率较高的情况下，随机采样的数据中通常都含有外点数据，因此，用含有外点的样本数据估计得到的模型参数常常含有较大误差。另外，在模型参数的检验过程中，寻找与该模型相容的样本数据时，一般方法是通过设定的阈值来判断的。若阈值设定过大，则会渗入大量的外点数据；若阈值设定过小，则检验过程会过分严格，进而筛选掉内点数据。因此，阈值的设定对算法的精度也有一定的影响。

综合分析，影响RANSAC算法计算精度的因素主要有两个：样本选择与阈值设定，而阈值一般是根据经验值进行设定的，目前没有更好的解决方案。若原始匹配点集合的质量较好，无论采用何种方式选择样本数据都能得到较好的估计结果，而事实上，到目前为止，没有一种算法可以完全消除外点的影响。要从根本上提高RANSAC算法的计算精度，需要较全面地检测和剔除外点数据。

三、改进RANSAC的基础矩阵估计算法

在基础矩阵的计算过程中，估计模型参数所需的样本数量基本是固定的，一般采用7点法或8点法来估计初始值。算法在保证一定置信概率的前提下，抽样次数与数据错误率有关，一旦数据错误率确定了，算法所需的抽样次数也就随之确定了，很难再改变。因此，通过上述分析，要提高基础矩阵的计算效率，可考虑从减少模型参数的检验时间入手，而预检验算法在不改变算法精度的前提下，可以很大限度地减小计算量，提高算法效率。根据前面对影响RANSAC算法精度的因素分析可知，检测并剔除外点数据是提高算法精度的关键，而一个好的模型参数更有利于检测出外点数据。提高RANSAC算法精度的一个可行方法是在样本选择时尽可能选择内点数据来估计模型参数。

1. 预检验

在RANSAC算法的计算过程中，大部分抽样都会受到外点的影响，对受到外点影响的这部分模型，每次都用全部数据去检验，这无疑浪费了大量的计算时间。预检验方法可有效减少模型参数的检验时间，其基本思想是：用少量样本数据来评估模型参数，如果该模型可以通过预检验，则认为当前模型是一个好模型，可接着进行后续的全部数据检验；否则认为该模型受到外点数据的污染，不再参与后续检验。加入预检验后，虽然不能改善算法精度，其精度与原RANSAC算法基本保持一致，而效率方面却可大幅提升。

2. 样本选择

采用传统RANSAC算法估计基础矩阵时，每次抽样都是一个相对独立的过程，并没有考虑前面已完成过程的反馈信息。而实际上，在前面已完成的抽样过程中，每次都需要对原始匹配点集中每个点是否为内点进行判断，对于每对匹配点质量的好坏，已经有了初步的判断。如果能够利用前面累积的反馈信息来指导下次抽样，这无疑将提高抽取样本的质量，从而可以更好地检测内点和外点数据。在多次循环验证的过程中，传统的RANSAC算法只记录每个基础矩阵初始值对应的内点总数，而实际上，在整个判断过程中可同时记录下每对点是否为内点。统计每对匹配点被标记为内点的次数，选择被标记为内点的次数较多的这部分点构成候选集合。在下一次样本抽取时，可直接从候选集合中进行。由于候选集合中的数据是根据被判断为内点的次数来确定的，因此，该集合的中的点作为内点的概率也大于其他点。每次验证过程结束后，需要重新计算每对匹配点被标记为内点的次数并更新候选集合，以便指导下一次抽样。

3. 算法过程

本文算法的基本思想是以传统RANSAC算法为框架，为提高算法效率与计算精度，结合预检验方法，选择被标记为内点次数较多的样本来估计基础矩阵初始值。计算过程可分为初始候选集合构成和内点集的确定两个部分，具体描述如下：

(1) 初始候选集合生成

1) 计算所需抽样次数K。

2) 在前K/3次抽样中，从原始匹配点集合中随机选择8个样本点，用改进的8点算法计算基础矩阵的初始值。

3) 加入预检验步骤，在对通过预检的初始值进行验证的过程中，计算对应的内点数量的同时标记每对匹配点是否为内点。

4) 完成K/3次抽样后，计算到目前为止每对匹配点被标记为内点的次数，选择被标记内点次数较多的匹配点对构成初始候选集合。

(2) 内点集确定

1) 在余下的抽样过程中，采用前面介绍的样本选择方法，从候选集合中选择最小子集来估计基础阵的初始值。

2) 结合预检验方法，若当前模型参数通过预检验，计算其对应的内点数量并重新计算初始集合中每对匹配点被标记为内点的次数。

3) 更新候选集合。

4) 完成K次抽样后，选择包含内点数量最多的集合作为内点集。

5) 根据确定的内点集，采用M-Estimators方法重新估计基础矩阵，并将结果作为最优值返回。

四、试验结果与分析

为了验证本文算法的有效性和鲁棒性，分别对大量的模拟数据和真实图像数据进行了试验，将本文算法与M-Estimators、LMedS和RANSAC 3种经典鲁棒方法进行对比，用点到对应极线的平均对极距离来精确反映基础矩阵的估计精度，对极距离越小，说明基础矩阵的估计精度越高。由于篇幅所限，本文直接给出部分试验结果。

1. 模拟数据和真实图像试验

模拟数据是采用程序生成同一场景不同视角两幅图像的匹配点对，数量为100。添加均值为0，方差为1.0的高斯噪声后，不同外点比率下4种算法的计算精度比较结果如图2所示。表1为在外点比率为20%的情况下，不同噪声下4种算法的计算精度比较。

图2 4种方法在不同比率外点数据情况下的平均对极距离

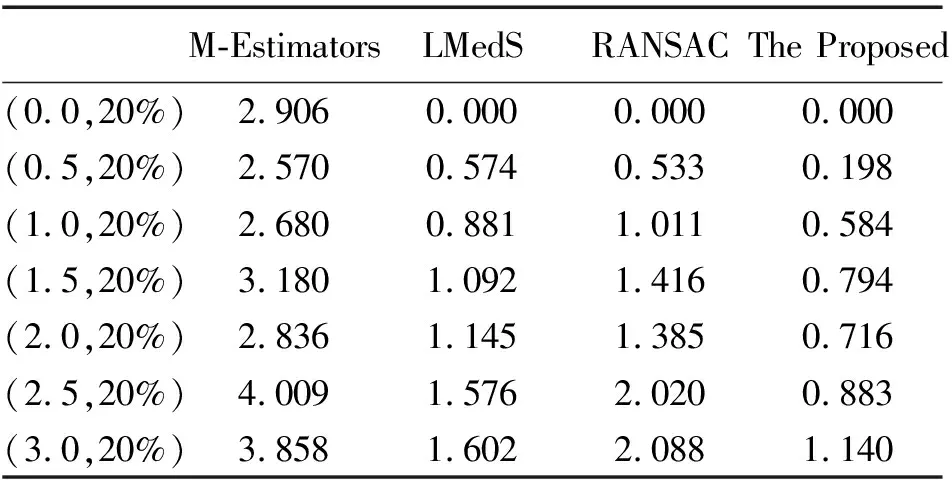
表1 不同噪声情况下的平均对极距离 像素

图3为采用SIFT算法对两幅图像进行特征提取与匹配获得初始匹配集合的效果图。其中，场景1包含的匹配点数量相对较多，共1247对；场景2包含147对，相对少一些。之所以选择这两幅图像，是由于其包含的匹配点数量有较大差别，可验证在不同匹配点数量下算法的鲁棒性。表2给出了每个场景通过上述4种算法获得的平均对极距离和标准偏差。

图3 两幅图像特征提取与匹配效果图

表2 4种方法对真实图像数据的计算结果 像素

2. 计算精度分析

从上述试验结果来看，无论模拟数据还是真实图像试验数据，本文算法的结果均优于其他3种方法。在不同比率的外点数据下，M-Estimators方法随着外点比率的增大误差最大，LMedS方法的精度略优于RANSAC方法，本文算法一直能保持较高精度。从表1的试验结果可以看出，随着噪声的增大，4种算法的精度都有所降低，M-Estimators方法受噪声影响最大。当噪声强度超过1.0时，LMedS方法和RANSAC方法的误差较大，而本文方法在噪声强度为3.0时，仍能保持较高的精度。从真实图像试验结果来看，无论匹配点数量的多少，本文算法的结果都优于其他3种方法。当匹配点数量较少，且外点率较高时，算法体现出更好的性能。

综合分析，本文算法的计算精度优于其他3种方法，这主要得益于两个方面：一方面是本文算法在样本选择时从被判断为内点次数较多的点中抽取样本点来估计模型参数，选择的样本点作为内点的概率较大，为下一步处理提供了较好的模型参数，可以更准确地判断内外点；另一方面是在获得内点集的基础上，采用M-Estimators方法迭代处理不断优化，进一步去除对结果影响较大的匹配点，从而提高了算法的估计精度。

3. 计算效率分析

为考察本文算法的计算效率，分别计算不同外点比率和不同匹配点数量下4种算法的计算时间。不同外点比率下算法的计算时间如图4所示，试验数据中添加有均值为0，方差为1.0的高斯噪声。不同匹配点数量下算法的计算时间以场景1为例，图5为试验结果。

从图4可以看出，在外点比率小于40%时，4种算法的计算时间差别不大，随着外点比率的增大，M-Estimators算法一直保持较高的计算效率，而RANSAC算法的计算时间呈指数增长；当外点比率超过50%时，除M-Estimators算法外，其他3种方法的计算时间会随着外点比率的增加而增大；当外点比率增加到60%时，本文算法所需计算时间远小于RANSAC方法与LMedS方法。从图5可以看出，随着匹配点数量的增多，4种算法的计算时间也随之增长，LMedS方法的计算时间增加最快，M-Estimators的计算时间虽然也有所增加，但其计算效率仍是4种方法中最高的。而本文算法的计算效率仍优于LMedS方法与RANSAC方法。

图4 不同外点比率下4种算法的计算时间

图5 不同匹配点数量下4种算法的计算时间

4. 本文算法与PARANSAC算法比较

鲁珊[10]等针对随机抽样一致性算法效率低的问题，提出了一种基于概率分析的随机抽样一致性算法(PARANSAC)。为进一步验证本文算法的精度与效率，将本文算法与PARANSAC算法对比，试验数据采用文献[10]中的真实图像数据，结果如图6所示。从表3的试验结果来看，本文算法在计算精度与效率上均优于PARANSAC算法。本文算法样本选择策略简单，不增加额外的计算开销，而PARANSAC算法在每次迭代过程中都需要计算每对匹配点的概率，并且在计算过程中需要设置合适的阈值，阈值设置不当将严重影响计算结果。

图6 不同角度的2组真实图像

表3 计算精度与效率比较

五、结束语

本文针对采用传统RANSAC算法进行基础矩阵计算时效率较低和样本选择随机性的问题，提出了一种改进RANSAC的基础矩阵计算方法。该算法通过加入预检验步骤去除明显错误的模型，减少了大量的无用计算，提高了算法效率。由于被标记为内点次数较多的点作为内点的概率要大于其他数据，因此，根据被标记为内点次数的多少为标准来指导后续抽样，提高了获得好的模型参数的概率，从而可以更好地检测并剔除外点数据。最后在确定内点的基础上，采用M-Estimators方法进一步提高解算精度。试验结果表明，本文算法不仅可以有效剔除错误匹配点，提高基础矩阵的计算精度，并且在鲁棒性和计算效率方面也较优。

参考文献：

[1] 宋宏权，刘学军，闾国年，等. 地理参考下未标定图像序列的三维点云精度分析[J]. 测绘通报，2012(7)：14-16,20.

[2] 季铮，张剑清，詹总谦. 基于序列影像和积分法的复杂物体三维重建[J]. 测绘通报，2008(1)：26-29.

[3] ARMANGUE X, SALVI J. Overall View Regarding Fundamental Matrix Estimation[J]. Image and Vision Computing，2003，21(2): 205-220.

[4] STEWART C V. MINPRAN: A New Robust Operator for Computer Vision:Application to Range Data[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1995, 17(10): 925-938.

[5] TORR P H S, ZISSERMAN A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry[J]. Computer Vision and Image Understanding, 2000, 78(1): 138-156.

[6] MATAS J, CHUM O. Randomized RANSAC withTd,dTest[J]. Image and Vision Computing, 2004, 22(10): 837-842.

[7] 陈付幸，王润生. 基于预检验的快速随机抽样一致性算法[J]. 软件学报，2005，16(8): 1431-1437.

[8] 田文，王宏远，徐帆，等. RANSAC算法的自适应Tc,d 预检验[J]. 中国图象图形学报，2009，14(5): 973-977.

[9] 刘坤，葛俊锋，罗予频，等. 概率引导的随机采样一致性算法[J]. 计算机辅助设计与图形学学报，2009，21(5):657-662.

[10] 鲁珊，雷英杰，孔韦韦，等. 基于概率抽样一致性算法的基础矩阵估计算法[J]. 控制与决策，2012，27(3): 425-430.