基于大林算法模型失配时滞控制系统的研究

，

(常州工学院电子信息与电气工程学院，江苏 常州 213000)

0 引 言

工业生产的大规模化使工业过程变得更为复杂，大时滞对工业过程控制系统的设计提出了更高的要求，因此需要更高级、更快速、更可靠和更有效的控制方法[1]。

在基于参数模型的控制方法中，Smith预估控制和Dahlin控制是最经典和最成熟的方法，它不仅使设定值和外部扰动输入的稳态误差为零，还可以结合很多智能控制方法形成各种改进的智能控制系统，提高控制的品质。对于时滞系统模型的不确定性，非参数模型显得更为有效，因此智能控制开始进入时滞系统，其中模糊控制和神经网络控制可以发挥很大的作用。神经网络有学习与适应严重不确定性动态特性的能力，并且具有很强的鲁棒性和容错性，模糊控制理论具有处理不精确信息的能力，从而使模糊控制能模仿人的经验对复杂被控对象进行专家式的控制，但是对于时滞过程，如何获得有效的控制规则仍然是一个难题。

自适应控制方法的出现又丰富了时滞系统的控制方法，它的其他方法结合形成了各种有效实用的新方法，有很大的优越性。鲁棒控制和变结构控制针对时滞控制系统的控制在理论上的研究也很成功，但他们计算复杂，有时会出现找不到解的情况，因此，其应用价值在当前仍然有限。因此，时滞系统的控制不是单一的方法就可以完善解决的，工业计算机的出现与完善可以很容易地实现各种复杂且高级的控制算法，因此，针对时滞过程的特点，开发与设计出各种智能控制方法或者以不同的形式结合在一起，将是解决工业时滞过程的有效途径[2-4]。

文中以工业生产中常见的退火炉系统为被控对象，通过大林算法对退火炉系统中出现的大时滞现象进行研究，解决热处理过程中的控制问题，得到大林算法在处理带有时滞的控制系统过程中的有效性。

1 退火炉系统的数学模型

煤气罩式退火炉包括内罩和外罩两个部分。其结构图如图1所示[5]。其中，外罩的作用是将整个炉结构和外部环境隔离，炉的内、外罩之间的空间充入空气和煤气混合气体并通过燃烧给系统供热。内罩用于隔离燃烧气体和工质，内罩的内部填充保护钢质的保护性气体，从而使得钢质不会因为受热发生氧化，保证了工质的纯度。另外，外罩和控制阀门通过煤气阀门连接，这样可以方便往罩里面充入燃烧气体。而内罩和保护气体阀门连接，使得可以往内罩的内部充入保护性气体而将燃烧过程作用于内、外罩之间。外罩的内侧镶嵌着喷嘴，混合的空气和煤气的混合气体通过喷嘴处释放，喷嘴总共12个，分上下两层分布。每一层中6个喷嘴相互交替的排列在内罩边上。两个蝶阀主要用来控制空气和煤气的燃烧比，调节蝶阀的不同开合程度就可以调节煤气和空气的混合比。当加热内罩的时候，需要保持煤气和空气的混合比和设定的数值一致。退火炉测量获得的温度数值实际上是退火炉内罩中保护性气体的温度。因为无法对退火炉内部的工质的温度进行直接测量，而工质位于保护性气体中，因而可以近似认为测量保护性气体的温度就是工质的温度。空气和煤气的阀门都是选用蝶阀，蝶阀的开关一般可以通过电机执行机构在连杆的作用下带动转动，进而可以自动实现阀门开度的自动调节。退火炉系统的输入是蝶阀的开度，输出为保护性气体问的近似值，整体构成一个单输入单输出的温度控制系统。

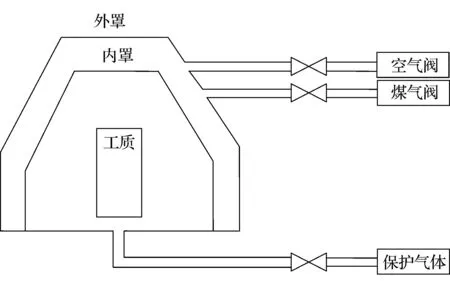
图1 罩式退火炉结构图

诸如退火炉这样带有特殊性质的控制对象，它的传递函数通常可以近似为一个一阶惯性加延时模型。一阶惯性加延时模型的系统传递函数表示为：

式中：K为退火炉比例环节系数(放大系数)；τ为退火炉的纯滞后时间；T为退火炉的时间常数。

通过阶跃响应曲线我们很容易得到系统的各个参数值：τ=0.76seconds，T=0.4，K=1，即系统的传递函数为：

2 大林算法设计数字控制器

大林算法是由美国IBM公司的大林( Dahllin) 于1968年针对工业生产过程中含纯滞后的控制对象的控制算法[6]。该算法的设计目标是设计一个合适的数字控制器，使整个系统的闭环传递函数为带有纯滞后时间的一阶惯性环节。如图2所示为退火炉温度控制系统的方框图。其中，Gc(z)代表数字调节器，Gp(z)代表零阶保持器，则系统的闭环传递函数表示为：

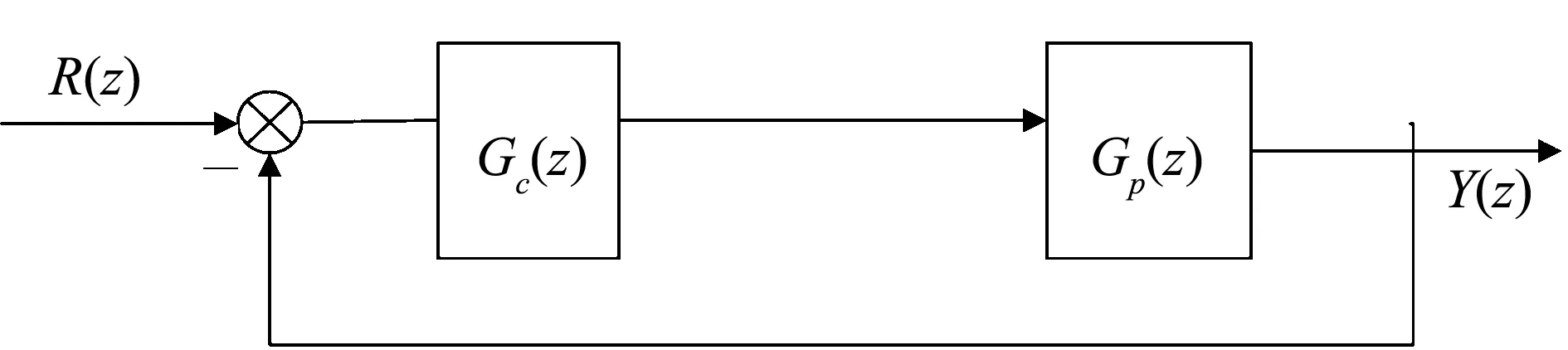
图2 退火炉温度控制系统方框图

则

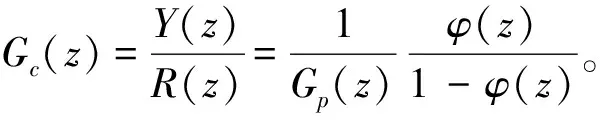
系统设计的最关键步骤就是要能设计数字控制器Gc(z)使得系统的闭环传递函数近似为具有纯滞后的一阶惯性环节，即：

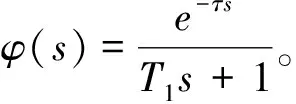
上式经过Z变换变为：

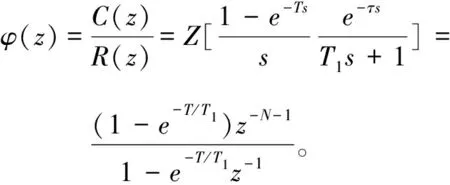
可求得调节器的传递函数：

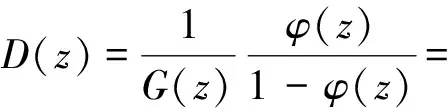
被控对象离散化得出函数：

数字控制器的离散传递函数为：

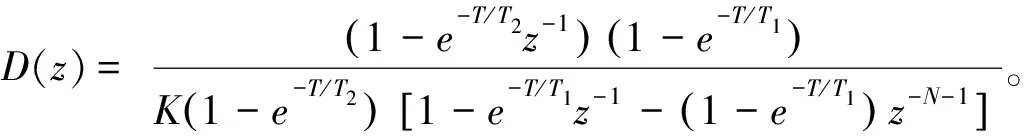
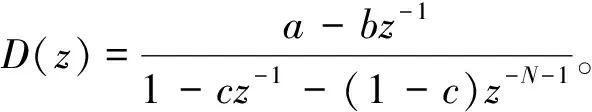
其中，数字控制器的系数为：

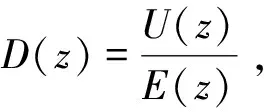
u(k)=cu(k-1)+(1-c)u(k-N-1)+

ae(k)-be(k-1)。

如图3所示为大林控制算法的流程图。

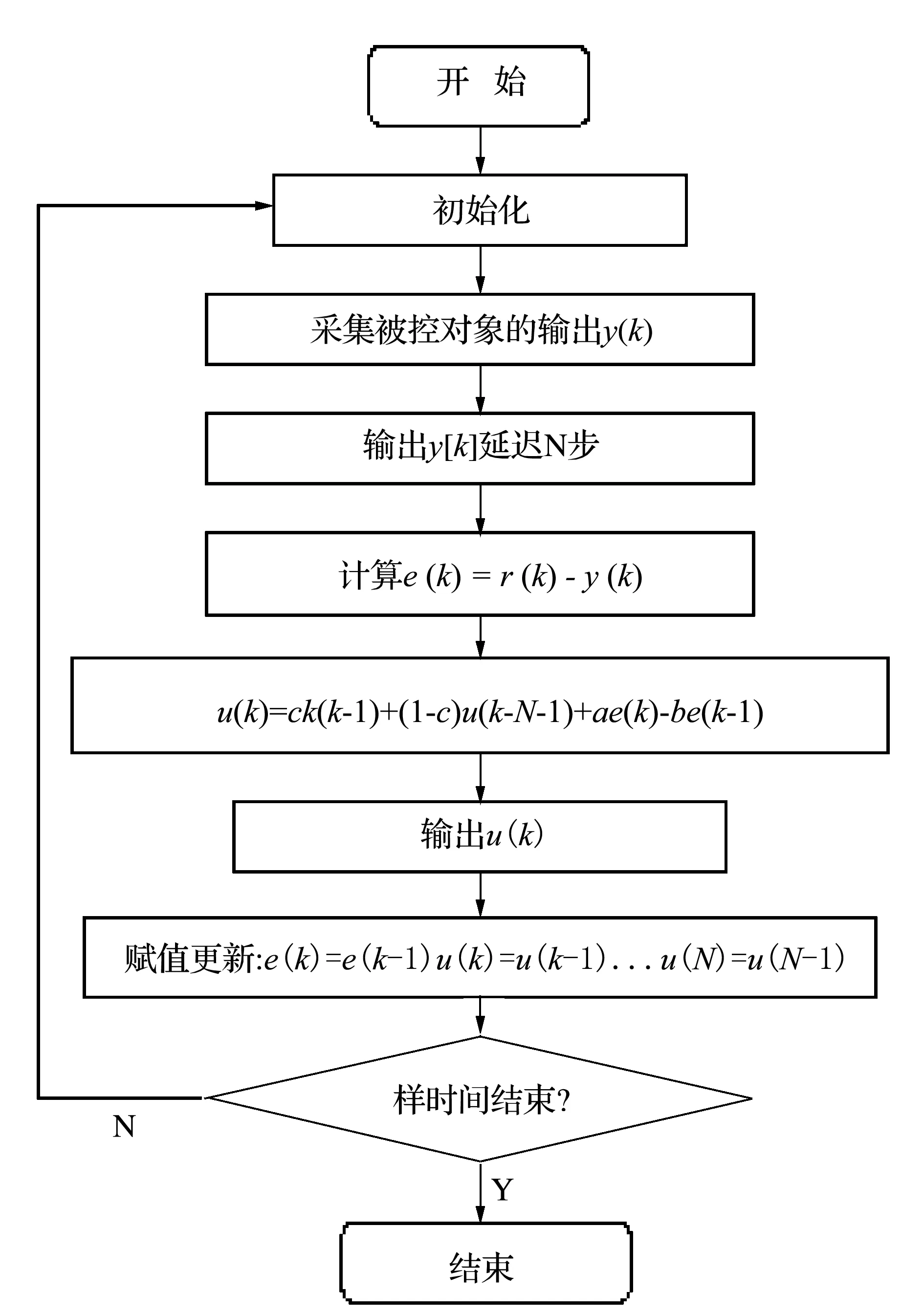
图3 程序流程图

首先对系统进行初始化，假定初始时刻控制器输出为零。从某一个采样时刻开始，系统进行对被控对象的输出y(k)进行采样并对输出采样值进行时长为N的延迟，接着计算系统e(k)=r(k)-y(k)误差，并由初始化得到的参数值带入计算公式中进行计算，使控制器的输出值作为控制对象的输入量，接下来每一个采样时刻作相同的动作，直到系统工作结束。

3 控制系统仿真

取采样时间为T=0.5 s，则系统可以离散化表示为：

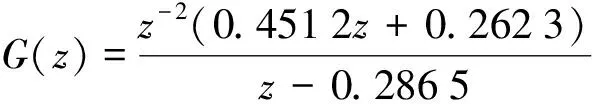
大林算法中的控制器的传递函数为：

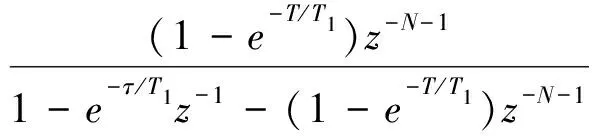
在MATLAB下编制M文件，输入信号采用单位阶跃信号，得到的仿真结果如图4所示。

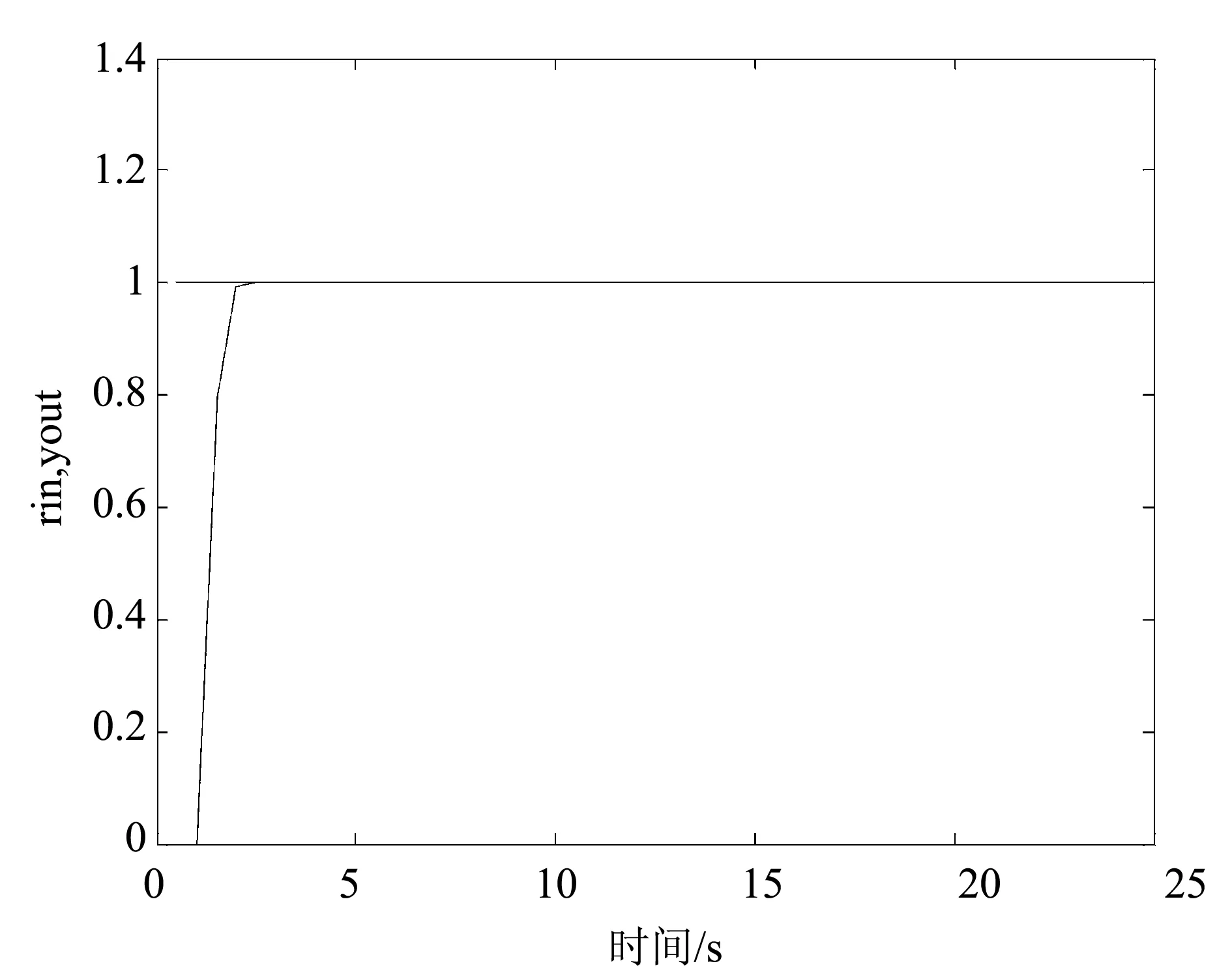
图4 大林控制算法仿真图

由图4可以发现，采用大林控制器进行系统控制时，系统非常稳定，在有限步内就实现了系统稳定，可以实现无超调。

当控制系统的数学模型发生参数失配时，当实际对象的传递函数的增益K=0.95，同时假定模型不准确但是控制器的参数不发生变化，可以得到如图5所示的仿真图。

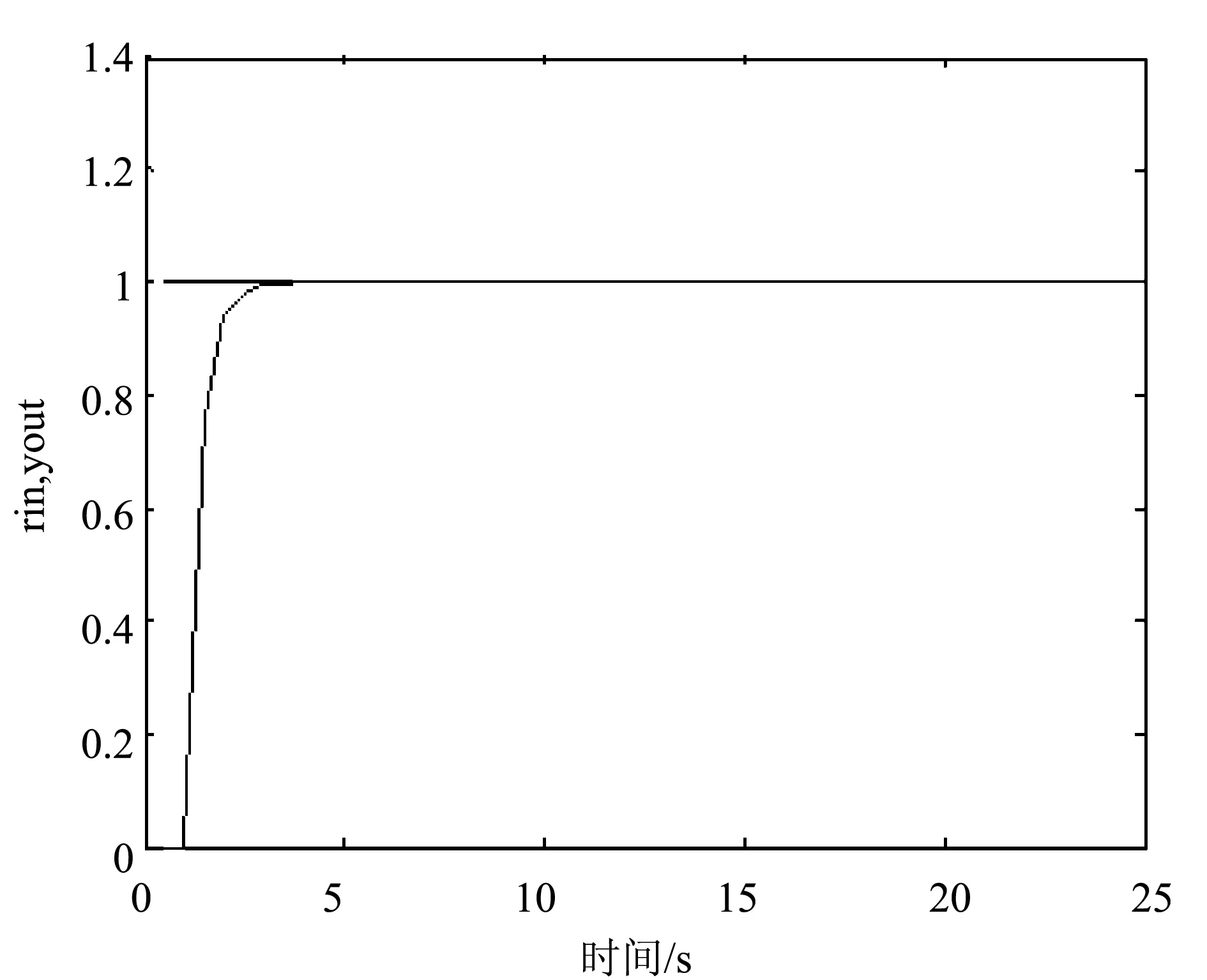
图5 参数K失配时控制效果

改变控制对象的惯性时间常数令T=0.38，保持其他的参数不变，并且使得控制器参数保持不变，系统的仿真图如图6所示。

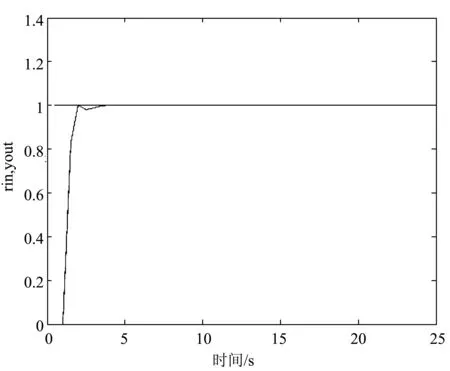
图6 参数T失配时控制效果

改变控制对象的惯性时间常数令τ=0.8，保持其他的参数不变，并且使得控制器参数保持不变，系统的仿真图如图7所示。

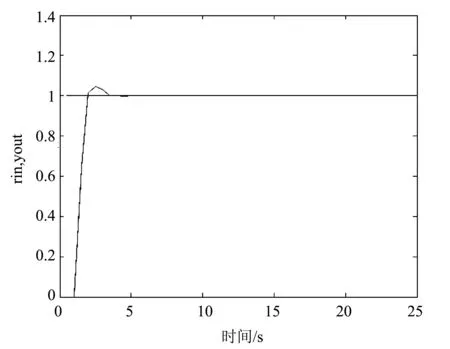
图7 参数τ失配时控制效果

控制参数在一定的范围内，同时改变三个参数，使K=0.95，T=0.38，τ=0.8，系统仿真图如图8所示。

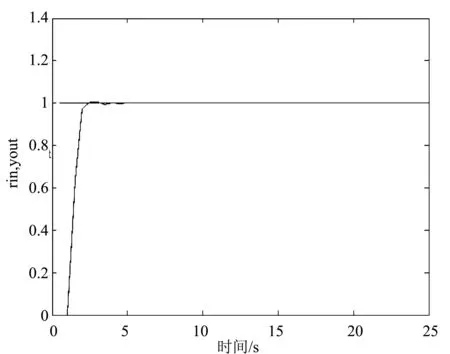
图8 模型全部失配时控制效果

由图5到图8可以发现，在系统参数发生失配时，大林算法可以很好实现带有纯滞后系统的控制，虽然在延时时间和惯性参数发生失配时系统出现超调，但是系统的超调很小，不影响系统的控制。

4 结束语

文中主要研究了大林算法对带有大时延的惯性系统的控制，采用退火炉为研究对象，运用大林算法设计了数字控制器，并且很好地控制了系统的性能。系统在有限步(2步)就实现了系统无误差控制，且系统响应没有超调量，整体动静态特定都很好。然后分别讨论了在被控制对象比例参数、惯性参数和延迟参数发生失配情况下系统的控制。通过仿真结果表明，在系统参数失配时，大林控制器仍然可以实现很好的控制。

[1] 谭永红.关于大林算法的一些研究[J].化工自动化及仪表，2010,17(4):57-61.

[2] 杨琳娟，李秋明，顾德英.大林算法在炉温控制中的应用[J].仪器仪表学报，2005,26(8): 450-454.

[3] 赵德元.电阻炉温度的大林算法控制[J]，成都大学学报(自然科学版)，2004，23(2):25-29.

[4] 郑剑翔.一阶惯性延时系统的免分析建模法_MATLAB在大林算法建模仿真中的应用[J].福州大学学报(自然科学版)，2007,35(1)：64-69.

[5] 刘建冬.带有大林算法的锅炉温度控制系统[D].上海：复旦大学，2009：27-34.

[6] 张燕红,张建生.计算机控制技术[M].南京：东南大学出版社，2008：95-98.