孔穴扩张理论对静力触探锥尖阻力一般解的推导

毛 玉 坤

(中交通力建设股份有限公司，陕西 西安 710075)

孔穴扩张理论对静力触探锥尖阻力一般解的推导

毛 玉 坤

(中交通力建设股份有限公司，陕西 西安 710075)

基于变形控制的孔穴扩张理论，推导了静力触探贯入过程中锥尖阻力的一般解的表达式，并利用一般解的表达式，通过算例计算了不同干密度、不同压缩模量对触探锥尖阻力的影响，得出了一些有参考价值的结论。

静力触探，孔穴扩张理论，贯入阻力

1 静力触探的理论研究进展

静力触探(cone penetration test)作为一种常用的原位测试方法具有速度快、数据连续、再现性好、操作简便等特点。随着静力触探技术的不断发展和延伸，在世界范围内的许多软土地区国家已经被广泛应用。由于我国静力触探技术起步较晚，在学术方面同国际上交流较少，因此在静力触探的机理研究上较世界先进水平还有一定差距。从已发表和出版的文章或著作中可以看出静力触探的理论研究不外乎以下几种：承载力理论、孔穴扩张理论、应变路径理论、有限元法等[1]。因此，静力触探技术不论在理论研究还是在实际应用中都有待于进一步研究。

目前，国内外研究学者在孔穴扩张理论研究中取得了丰富的研究成果[2-6]。本文采用孟高头教授提出的基于变形控制的孔穴扩张理论，推导了静力触探贯入过程中锥尖阻力的一般解的表达式，并利用一般解的表达式，通过算例计算了不同干密度、不同压缩模量对触探锥尖阻力的影响。

2 基于变形控制的孔穴扩张理论解的求解

基于变形控制的孔穴扩张理论是以初始无穷小的球穴受到均布内压作用，在无限介质中匀速扩张(指球面外推速率恒定)来模拟探头在土中的贯入。通过几何方程并考虑应力、应变，根据弹塑性交界处应力连续条件来求解内压pu,用求出的内压来计算触探端阻qc。具体过程如下。

2.1 模型假设及参数选取

为了方便计算，推导过程中假设土体为弹性完全塑性介质，各向同性且具有相同的初始压力p0，塑性区不发生体积变形，并服从Tresca屈服条件。此外，计算中假设土体的贯入速度为U，锥角为α。因此，土的扩张模型如图1所示。

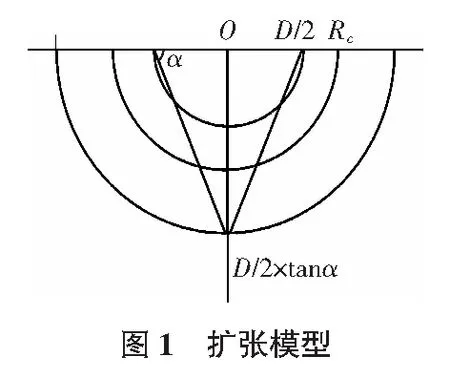
2.2 锥尖阻力一般解的推导

1)最终半径Rc的选取：

(1)

2)土体服从Tresca屈服条件：

σ1-σ3=2Cu

(2)

3)计算时采用球坐标系。设t0时刻球穴半径为Ru，弹塑性界面半径为Rp，内压为Pu。经过时间dt后，球穴半径增至R′=Ru+Vdt，孔壁处的径向位移为uR=-Vdt；界面半径增至Rp′，内压为Pu′。

4)应力、应变以压为正，根据小应变理论，则几何方程为：

(3)

其中，εr，εθ，εφ分别为径向、环向和切向应变。

因为塑性区内无体变，则体积应变εv为：

(4)

解此常微分方程，并结合边界条件u|r=Ru=uR，得径向位移u：

(5)

由式(5)可得弹塑性分界面Rp处的位移up为：

(6)

5)根据弹性定律Lame方程，弹塑性界面位移为：

(7)

其中，v为泊松比；E为弹性模量；σp=σr|r=Rp。又在交界处的应力应满足屈服条件式(2)，即：

σr-σθ=2Cu

(8)

又应满足球穴扩张的弹性解，即：

(9)

于是，结合式(8)，式 (9)得：

(10)

(11)

联解式(6)，式(11)得：

(12)

则有：

(13)

其中，εθR为孔壁处的环向应变。

6)根据弹塑性交界处应力连续条件来求解内压Pu。

在塑性区内，应力必须满足平衡方程：

(14)

又要服从屈服条件，现将屈服条件式(2)代入式(14)，并积分得：

σr=C-4Culnr

(15)

按孔穴内壁应力边界条件σr|r=Ru=Pu，得积分常数C：

C=Pu+4CulnRu

(16)

将式(16)代入式(15)，得塑性区内径向应力σr为：

(17)

因此，弹塑性交界处径向应力为：

(18)

将式(10)代入式(18)，得内压Pu为：

(19)

7)由式(19)可计算经过时间dt后，球穴由Ru等速扩张到Ru′时达到的内压Pu′，即：

(20)

将式(12)，式(13)代入式(20)，化简得：

(21)

(22)

8)最后根据式(22)得到的球穴扩张的内压来计算触探端阻qc。

取扩张至最终半径Rc的下半球，其内压Pu′在竖直方向上分力的合力即为轴力Q。Pu′在竖向的分力为Pu′cosφ，则：

(23)

积分得：

(24)

将轴力换算为探头圆锥底面的单位面积应力qc，则：

(25)

(26)

式(26)即为基于变形控制的球穴扩张理论推导的求解锥尖阻力的解的一般表达式。

9)需要说明的是：利用式(26)计算qc时，需先确定初应力P0和孔壁处的环向应变εθR。

首先，初始应力P0的确定:

(27)

3 算例分析

利用前面推导的计算触探锥尖阻力的一般解析式，通过计算来分析土的物理性质指标中密度和压缩性对触探锥尖阻力的影响。

在进行计算分析时，触探参数选用α=60°，D=35.7mm，U=2cm/s；土材料的基本参数选用c=20kPa，φ=24.5°。在地表附近一定厚度的土层(30cm～50cm)范围内，由于受阳光照射，土的含水量较低，土质比较坚硬，同时一般覆盖有植被及建筑垃圾等填充物。因此，计算时将不计地表以下50cm范围内的触探阻力。

3.1 密度对锥尖阻力的影响

图2为压缩模量E=2MPa时，干密度分别为1.35g/cm3,1.55g/cm3,1.75g/cm3时，锥尖阻力随深度变化的关系曲线。从图2中可以看出，锥尖阻力随密度的增大而增大，并且随深度的变化愈加明显。

3.2 压缩性对锥尖阻力的影响

图3的干密度为1.55g/cm3，压缩模量分别为2MPa,3MPa,4MPa时，锥尖阻力随深度变化的关系曲线。从图3中可以看出，锥尖阻力与土的压缩性也有关，压缩模量越大，土越密实则锥尖阻力越大，反之亦然。

4 结语

本文以基于变形控制的孔穴扩张理论为基础，通过简化的力学模型和Tresca强度屈服准则，推导了静力触探贯入过程中锥尖阻力的一般解析解。应用该理论结果，通过典型算例，计算了土材料在不同干密度和压缩模量下的锥尖阻力值，绘制了不同干密度、不同压缩模量下锥尖阻力与贯入深度之间的关系曲线。计算表明，静力触探锥尖阻力随干密度的增大而增大，随着压缩模量的增大也逐渐增大的结论。同时验证了静力触探的锥尖阻力影响因素不仅与触探设备的尺寸大小(如锥角、锥径)等因素有关，同时还与被研究对象本身的物理力学性质指标密切相关。

[1] 孟高头.土体原位测试机理方法及其工程应用[M].北京:地质出版社,1997.

[2] 王晓鸿,王家来,梁发云.应变软化岩土材料内扩孔问题解析解[J].工程力学,1999,16(5):71-76.

[3] 罗战友,厦建中,龚晓南.不同拉压模量及软化特性材料的球形孔扩张问题的统一解[J].工程力学,2006,23(4):22-27.

[4] 王延斌,范 文,徐栓强.基于统一强度理论的柱形孔扩张问题研究[J].岩土力学,2003,24(sup):125-132.

[5] 汪鹏程,朱向荣,方鹏飞.考虑土应变软化及剪胀特性的大应变球孔扩张的问题[J].水利学报,2004(9):78-82.

[6] 梁发云,陈龙珠.应变软化Tresca材料中扩孔问题解答及其应用[J].岩土力学,2004,25(2):261-265.

On deduction of cavity expansion theory in general solution to tip resistance of static sounding

MAO Yu-kun

(ZhongjiaoTongliConstructionCo.,Ltd,Xi’an710075,China)

Based on the deformed and controlled cavity expansion theory, the paper deduces the general solution to the tip resistance in the penetration process of the static sounding, and concludes some valuable reference by adopting the general solution and calculating the influence of the various densities and modulus of compression on the sounding tip resistance.

static sounding, cavity expansion theory, penetrating resistance

1009-6825(2014)11-0092-03

2014-01-24

毛玉坤(1980- )，男，硕士，工程师

TU459

A