SVPWM过调制算法磁链分析及在永磁同步电机驱动中的应用*

杨澜倩, 唐 校, 万 频, 王永华, 杨向宇

(1. 广东工业大学 自动化学院，广东 广州 510006； 2. 华南理工大学 电力学院，广东 广州 510640)

0 引 言

现代电机普遍采用DC/AC供电模式。电机的运行性能很大程度上取决于逆变器输出电压的范围和品质。采用空间矢量脉宽调制(Space Vector Pulse Width Modulation， SVPWM)过调制方式可以提高直流电压利用率，扩展逆变器输出电压的范围。已有不少文献[1-5]对SVPWM过调制算法进行了探讨，多是集中在算法的改进上，较少对与SVPWM密切相关的定子磁链在过调制时的特性进行系统分析。本文依据文献[4]所提的一种简单算法，分析了各阶段的定子磁链特性。将该过调制策略应用于永磁同步电机的驱动中，对电机的运行特性进行了仿真研究。

1 SVPWM电压矢量与磁链矢量的关系

通过调节电机相电压可以改变作用于相绕组的磁动势和磁场，电压本身没有空间的含义，将外加相电压与相绕组所产生的磁动势联系起来时，电压才被赋予了空间含义[6]。SVPWM控制实质是磁链跟踪控制。依据伏秒平衡原理即磁链等效原理，由基本开关矢量合成得到等效的参考电压矢量。SVPWM的基本电压空间矢量如图1所示。

图1 SVPWM基本电压空间矢量

当忽略定子压降时，定子合成电压与合成磁链空间矢量之间的关系为[7]

(1)

即为

Δψs=usΔt

(2)

式(2)说明定子磁链的变化量与作用的电压矢量方向一致，大小等于电压矢量对时间的积分。在时间t内，定子磁链可以由式(3)计算得

(3)

式中:φ——电压矢量us的相角；

ω——us的角速度。

2 SVPWM过调制算法

为了提高逆变器直流侧的电压利用率，常常需要采用过调制方式。SVPWM所能调制输出的电压矢量限制在图1所示六边形内，对超出六边形边界的矢量无法实际跟踪，需要采用合适的电压矢量代替目标矢量。这就是过调制的内涵。矢量包含幅值和相角两个因素，不同的过调制策略是对这两个因素进行不同的处理，以达到较佳的输出效果。在输出效果相近的情况下，力求算法的简捷易实现。

图2 SVPWM过调制原理图

SVPWM过调制原理图如图2所示。图2所示为第一个扇区情况，其他扇区与此作相同处理。三角形OBH对应图1六边形的一个区域，实际输出的电压矢量与参考电压矢量等效。算法将过调制区域分成两个部分： 第一部分为三角形BHF范围，将这个范围内的参考电压矢量压缩至BH边，实际输出电压矢量的幅值改变，而相角不变；另一部分为三角形BHF外的部分，当参考电压矢量位于这个区域时，实际输出的电压矢量为某个基本电压矢量，相对参考电压矢量，实际输出矢量的幅值和相角都发生改变，在这个区域是保持最大电压矢量输出，即全范围内称为“六阶梯波”的调制方式。文献[4]中所提方法通过基本矢量的作用时间对两个区域进行判断，而无须进行保持角的计算，使整个过调制算法变得简单易于实现。

3 SVPWM各阶段磁链的形状和大小

以电压矢量和磁链矢量的关系，分析SVPWM各阶段的磁链形状和大小(以参考电压矢量us的大小划分)。

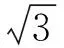
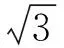
(4)

如果参考电压矢量幅值一定且旋转的速度恒定，其产生的磁链矢量轨迹是标准的圆形，磁链圆的大小与电压矢量旋转的速度成反比，相角滞后电压矢量相角π/2，磁链矢量圆的圆心比电压矢量圆的圆心要高，如图3所示。

图3 us≤Udc/时的矢量轨迹图

如图2中圆弧2所示，参考电压矢量位于该区间且匀速旋转一周时，实际输出的电压矢量将有一部分是圆弧，该部分可以跟踪参考电压矢量；另一部分位于六边形的边上，该部分对参考电压矢量进行了处理。由其积分产生的磁链矢量轨迹将不是标准的圆形，而是部分为椭圆形轨迹，如图4所示。六边形边上的矢量大小改变，故其积分值是一段椭圆弧，但是一个周期的磁链形状仍非常接近圆形。

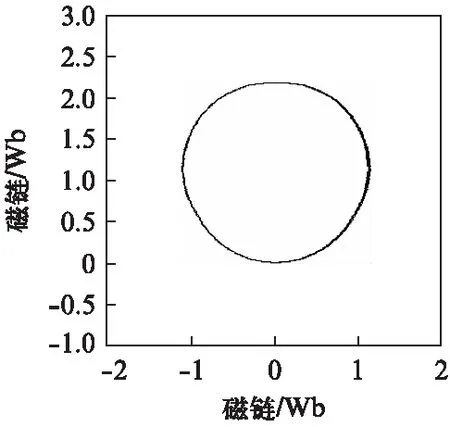
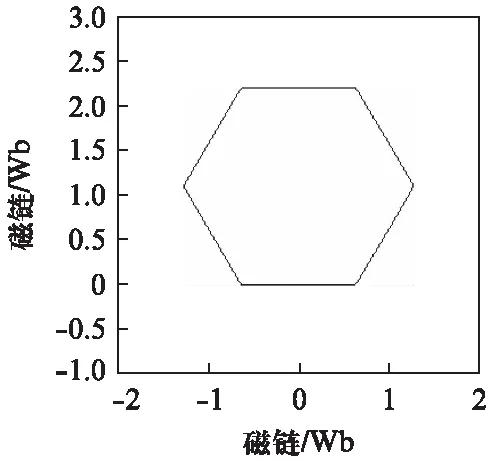
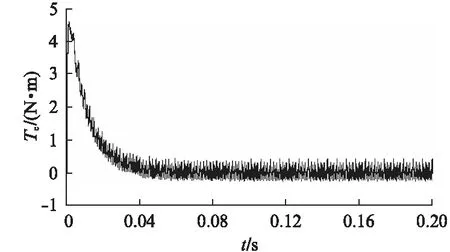
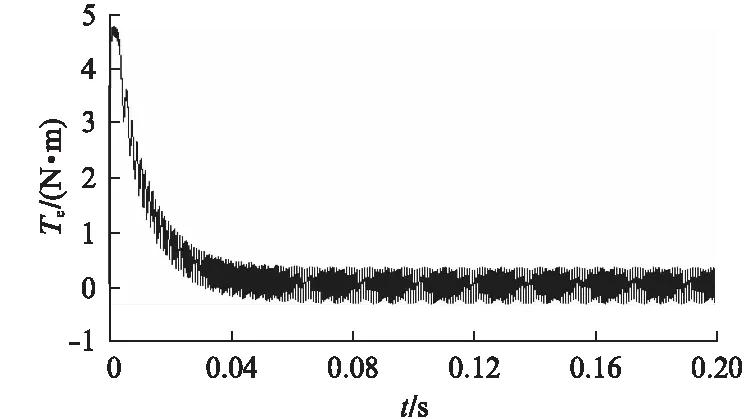
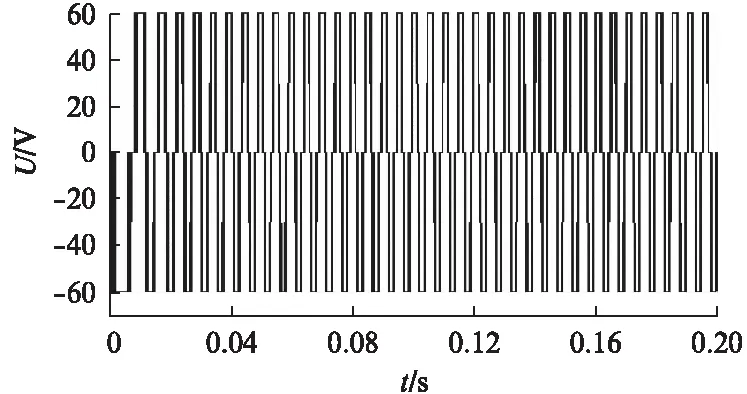
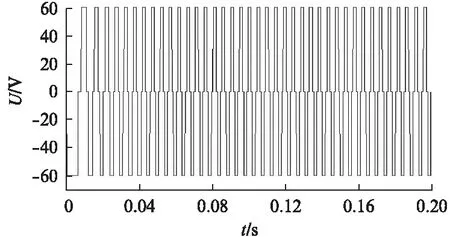
图

如图2中的圆弧3所示，参考电压矢量位于该区间时，实际输出的电压矢量均无法跟踪参考电压矢量。实际输出电压矢量有一部分是基本电压矢量(大小等于2Udc/3)单矢量输出，还有一部分被压缩到图1所示电压矢量六边形的边上。单独某个基本矢量作用时，虽然电压矢量不变，但是在其作用下的磁链却是运动的，且轨迹为直线。该情况下，当参考电压矢量匀速旋转一周时，所产生的磁链矢量轨迹包含有直线和圆弧部分，如图5所示。

图

如图2中圆弧4所示，在该情况下，实际输出的电压矢量是图1电压矢量六边形的6个顶点处的基本电压矢量，此时单相电压即为6阶梯波样式，如图6所示。电压矢量不变时，其积分产生的磁链是直线形，故该情况下，磁链矢量轨迹为正六边形。六边形的大小由参考电压矢量的旋转速度决定，速度越快，六边形越小。

图即六阶梯波时磁链轨迹图

4 过调制策略在永磁同步电机驱动中的应用

永磁同步电机在现代工业中应用越来越广泛。将过调制策略应用在其驱动中，可以加快电机的瞬态响应速度，并拓宽电机运行速度的范围。但过调制下的磁链轨迹不是标准圆形，故电磁转矩将存在脉动情况。永磁同步电机的电磁转矩te可表示为

te=pψs×is=pψsiT

(5)

(6)

式中:p——极对数；

iT——定子转矩电流分量；

Ls——定子等效自感；

ψf——转子永磁磁链；

δsf——负载角。

由式(5)可知，当定子磁链幅值不恒定时，电磁转矩不再与转矩电流分量iT成线性关系。由式(6)可知，过调制增大了定子磁链，从而增大了电机的输出转矩。由于ψs幅值改变，负载角不变时，将引起电磁转矩的变化。由过调制各阶段磁链形状可知，随着过调制程度的加深，磁链从圆形过渡到六边形，一个周期磁链变化量逐渐变大，导致转矩的波动变大。

在MATLAB/Simulink环境下搭建模型，对应用过调制策略后的永磁同步电机运行特性进行了仿真研究，并与没有采用过调制时的电机运行特性进行了对比。仿真模型采用三相全桥电路，逆变器直流侧电压为60V，永磁同步电机空载，给定转速为500r/min。其中的过调制策略采用S函数编写。仿真模型中，永磁同步电机的参数如表1所示。

表1 永磁同步电机的参数

未过调制、过调制时的永磁同步电机速度曲线分别如图7、图8所示。由于受制于直流侧的电压，电机转速未能达到给定转速。对比二者可知： (1) 过调制时，由于进一步提高了直流侧电压率，提高了电机的最大速度；(2) 过调制时，电机输出力矩增大，速度响应比未过调制时快。

图7 未过调制时永磁同步电机速度曲线

图8 过调制时永磁同步电机速度曲线

未过调制、过调制时的永磁同步电机转矩曲线分别如图9、图10所示。从图中可以发现，电机在过调制处理时的转矩脉动增大。

图9 未过调制时永磁同步电机转矩曲线

图10 过调制时永磁同步电机转矩曲线

未过调制、过调制时的永磁同步电机线电压波形分别如图11、图12所示。图11显示逆变器在一个采样周期中输出电压为PWM模式，由基本电压合成。图12对应的电机相电压为6阶梯模式，这种情况是逆变器能够输出的最大电压。

图11 未过调制时永磁同步电机线电压波形

图12 过调制时永磁同步电机线电压波形

5 结 语

SVPWM控制与电机定子磁链密切相关。本文从电压矢量与磁链矢量的关系出发，分析了一种过调制策略各阶段的磁链形状和大小。定子磁链直接关系到电机的运行性能，采用过调制策略应用于电机驱动，能加快电机的响应过程，拓宽电机运行速度的范围。本文的结论可为过调制策略在电机运动控制中的应用提供参考。

【参考文献】

[1] JOACHIM H. Pulsewidth modulation—A survey [J]. IEEE Transactions on Industrial Electronics, 1992,39(5)： 410- 420.

[2] 王旭东，张思艳，余腾伟，等.SVPWM过调制中控制角算法的分析与应用[J]. 电机与控制学报，2010,14(12)： 63- 67.

[3] 李计亮，高琳，刘新正，等.过调制算法在永磁同步电机弱磁调速系统中的应用[J]. 微电机，2010,43(12)： 43- 47.

[4] 吴芳，万山明，黄声华，等.一种过调制算法及其在永磁同步电动机弱磁控制中的应用[J]. 电工技术学报，2010,25(1)： 58- 63.

[5] JIDIN A, IDRIS N, ABDULLAH A R, et al. A hybrid DTC-DSC drive for high performance induction motor control [J]. Journal of Power Electronics, 2011,11(5): 704-712.

[6] 王成元，夏加宽，孙宜标，等.现代电机控制技术[M].北京： 机械工业出版社，2008.

[7] 阮毅，陈伯时. 电力拖动自动控制系统——运动控制系统[M]. 4版.北京： 机械工业出版社，2009.