基于小波变换的爆破振动信号不同频带能量分析
王 涛 夏岸雄 廖新旭
(1.广东宏大爆破股份有限公司,广东 广州 510623;2.武汉理工大学资源与环境工程学院,湖北 武汉 430070)
基于小波变换的爆破振动信号不同频带能量分析
王 涛1夏岸雄2廖新旭1
(1.广东宏大爆破股份有限公司,广东 广州 510623;2.武汉理工大学资源与环境工程学院,湖北 武汉 430070)
针对爆破振动信号持续时间短、突变性快的非平稳特征及振动信号三向传播特征,结合某露天矿逐孔爆破实测数据,利用小波分析技术,分析某点实测轴向、径向、垂向三向振动信号分频能量分布特征。研究结果表明:频带能量的最大值与质点峰值振速基本处于相同位置,总体成正比例关系,个别频带能量最大值并不处于峰值振速位置;逐孔起爆三向振动信号在不同频带能量分布不同,各向能量主要集中在250 Hz以内,250 Hz以后能量基本消失;由于周围建(构)筑物固有频率较低,据爆源140 m处振动数据的能量主要集中在15 Hz以上,因此,此次爆破共振对建(构)筑物的影响较小。研究结果为爆破振动安全评价提供了新的途径。
逐孔爆破 振动监测 振动信号 小波变换 分频能量
爆破振动信号是一种非平稳随机信号。对其进行监测及评价,在优化爆破参数时有重要的指导意义。近年来,随着小波理论及小波包理论的发展,振动信号可在时域-频域做细致分析[1-3],逐步完善着爆破振动理论。同时,随着监测仪器的更新,在监测振动信号时可同时监测某点三向振动信号。作者利用小波技术对三向振动信号能量分布特征进行对比分析,从不同角度评价爆破振动信号,使得爆破振动安全评价进一步完善。
1 小波分析原理
小波分析是在Fourier变换的基础上发展起来的,随着二进制小波快速算法的发展,逐渐走向了实用化。小波分析可在局部范围内对时域-频域信号进行动态调整。它对高频信号具有较高的时间分辨率和较低的频率分辨率;对低频信号具有较高的频率分辨率和较低的时间分辨率。其分析原理如下:
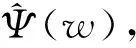
(1)
时,称Ψ(t)为一个母小波。
对任意函数f(x)∈L2(R)的连续小波变换为
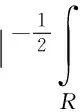
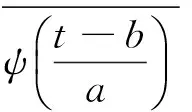
(2)
时,连续小波变换的逆变换为
b.
(3)
对于爆破振动信号,监测结果是由不同时间点对应的振动速度所组成的离散函数。每个时间点间隔时间极短,一般在0.02~1 ms,因此爆破振动信号为离散信号。在用式(2)计算时,必须对参数a、b进行离散化。在实际应用中,采用二进小波快速算法实现离散小波变换。取a=2j,b=2jk,j,k∈Z(自然数),由此得到二进小波函数
ψj,k(t)=2-j/2ψ
(2-jt-k).
(4)
二进小波变换为
W2jf(k)〈f(t),ψ2j
(k)〉=
(5)
二进小波变换的逆变换为
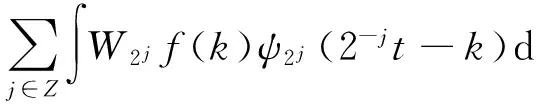
(6)
将二进离散小波变换尺度按指数等间隔划分。设分析信号的频带范围为(0,W);第一层分解后得低频a1(0,W/2)和高频d1(W/2,W);继续分解低频a1(0,W/2),得到低频a2(0,W/4)和高频d2(W/4,W/2);依次类推,分解N次(尺度为N)即可得到N层的小波分解结果,如图1所示。
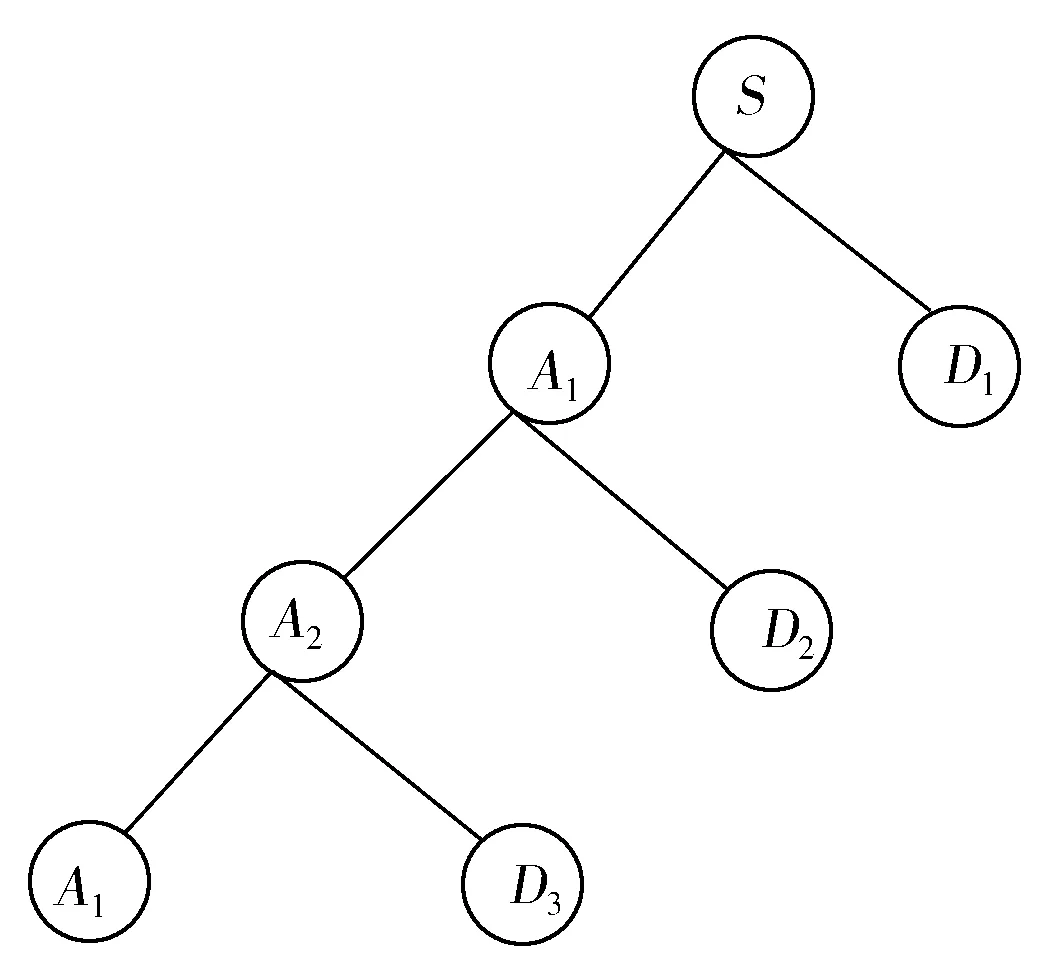
图1 二进离散小波三层分解Fig.1 Binary discrete wavelet decomposition
2 爆破振动信号频带能量表征
2.1 爆破振动信号小波分解
由二进小波分析原理可知,信号可以无限地进行分解。因此,信号分解之前,要确定信号分解深度。受到技术的限制,爆破振动信号监测仪有最小工作频率。因此,要保证信号频率处在最小工作频率范围内,否则将导致信号失真。本次测振试验所使用的TC-4850测振仪最小工作频率为5 Hz,爆破振动的频率一般低于200 Hz。根据仪器本身的特性及采样定理,信号的采样频率设为8 000 Hz,则其奈奎斯特(Nyquist)频率为4 000 Hz。因此,根据小波分析原理,将信号分解成9层,得到10个频带,分别为0~7.812 5 Hz、7.812 5~15.625 Hz、15.625~31.25 Hz、31.25~62.5 Hz、62.5~125 Hz、125~250 Hz、250~500 Hz、500~1 000 Hz、1 000~2 000 Hz、2 000~4 000 Hz。
2.2 小波基函数的选择
小波分析中,选择合适的小波基函数是首要考虑问题。根据前学者的研究[5-9],在众多的小波基函数中,利用Daubechies函数系列在分析爆破振动信号时,重构信号与原始信号相对误差最小,尤其是db8小基函数,完全适合于工程需要。此次选择db8小波基函数作为所选基函数。
2.3 小波分频能量分布
将爆破振动信号s(t)进行9层小波分解和重构。受信号的采样点数量限制,振动信号各频带Si对应的能量为
(7)
式中,xi,k(i=1,2,…,n,k=1,2,…,m,m为信号的离散点数)表示重构信号Si的离散点的幅值。则被分析信号的总能量为
(8)
不同频带爆破振动分量的相对能量分布为
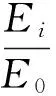
(9)
3 逐孔爆破振动信号各频带能量分析
3.1 爆破振动信号的选择
爆破振动受到诸多因素的影响,不同的爆破方式产生的振动效应大不相同。对于逐孔起爆技术而言[10],其单孔药量控制、微差时间、爆区地质环境及监测点布置方式为主要考虑因素。爆破振动信号选取应尽量排除无关因素的影响。利用TC-4850爆破振动监测仪对某露天矿台阶爆破振动监测,监测信号为水平径向、水平切向、垂直方向的三向振动信号。选取距爆源140 m处有代表性的数据,对其进行频带能量特征分析,探寻不同方向振动信号能量的集中频带。振动监测数据如表1所示。振动波形如图2所示。
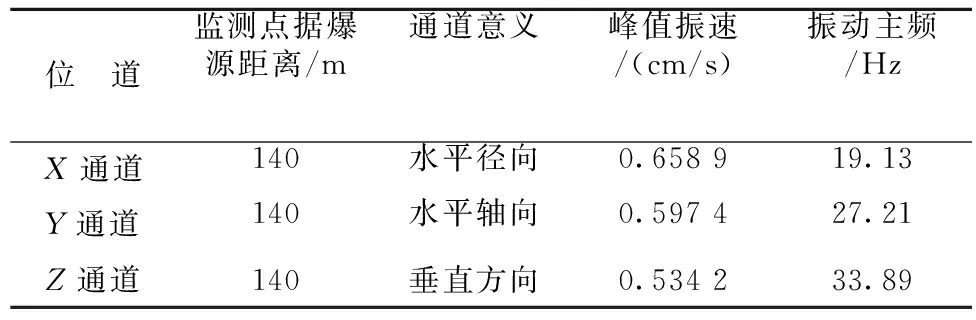
表1 逐孔爆破振动监测数据Table 1 Vibration monitoring data of hole by hole blasting
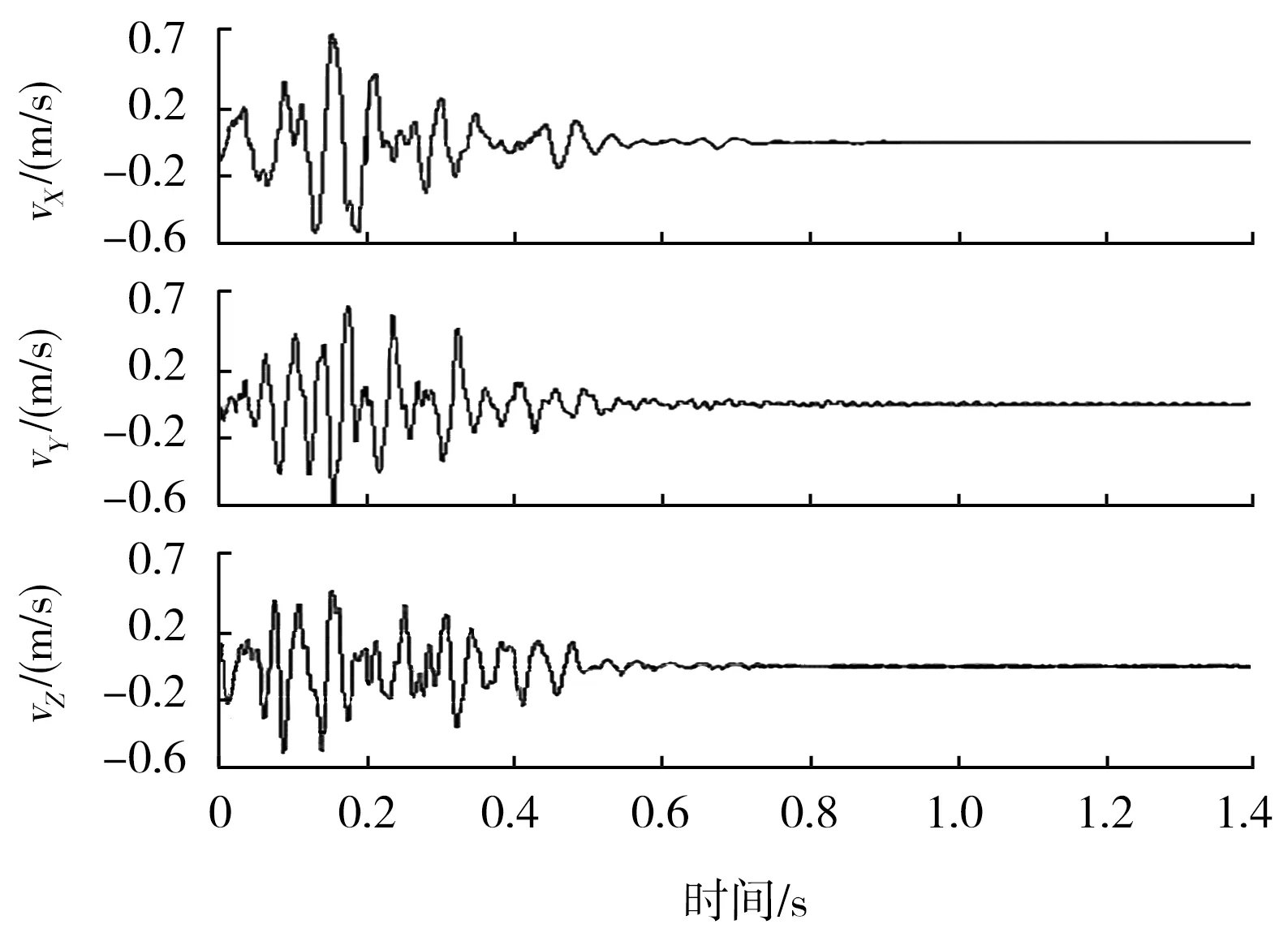
图2 振动波形监测Fig.2 Vibration waveform monitoring chart
3.2 爆破振动频带能量分析
(1)爆破振动信号具有持时短,突变快的特征。X、Y、Z三向峰值速度基本在0.18 s同时出现,随后振动信号迅速衰减。如图2所示。
(2)爆破振动信号频带能量的最大值与质点峰值振速基本处于相同位置,总体上成正比例关系;但个别频带能量最大值并不处于峰值振速位置,如图3、图4、图5所示。
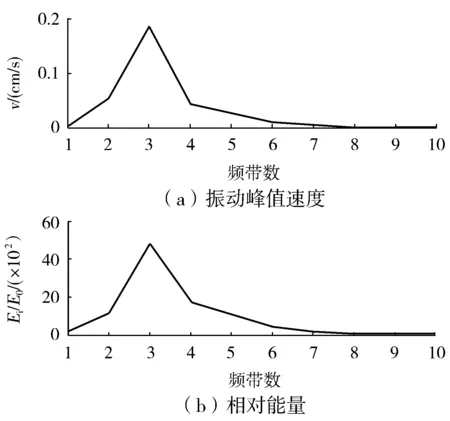
图3 水平径向不同频带下质点振动峰值速度和相对能量分布Fig.3 Different frequency bands peak particle velocity and relative energy distribution of horizontal radial
(3)对据爆源140 m处逐孔起爆爆破振动信号能量分析:振动信号能量主要集中在第三、第四频带范围,即15~60 Hz范围,250 Hz以后能量基本消失。由于周边建(构)筑物固有频率很低,因此,此次爆破共振对周围建(构)筑物的影响很小。
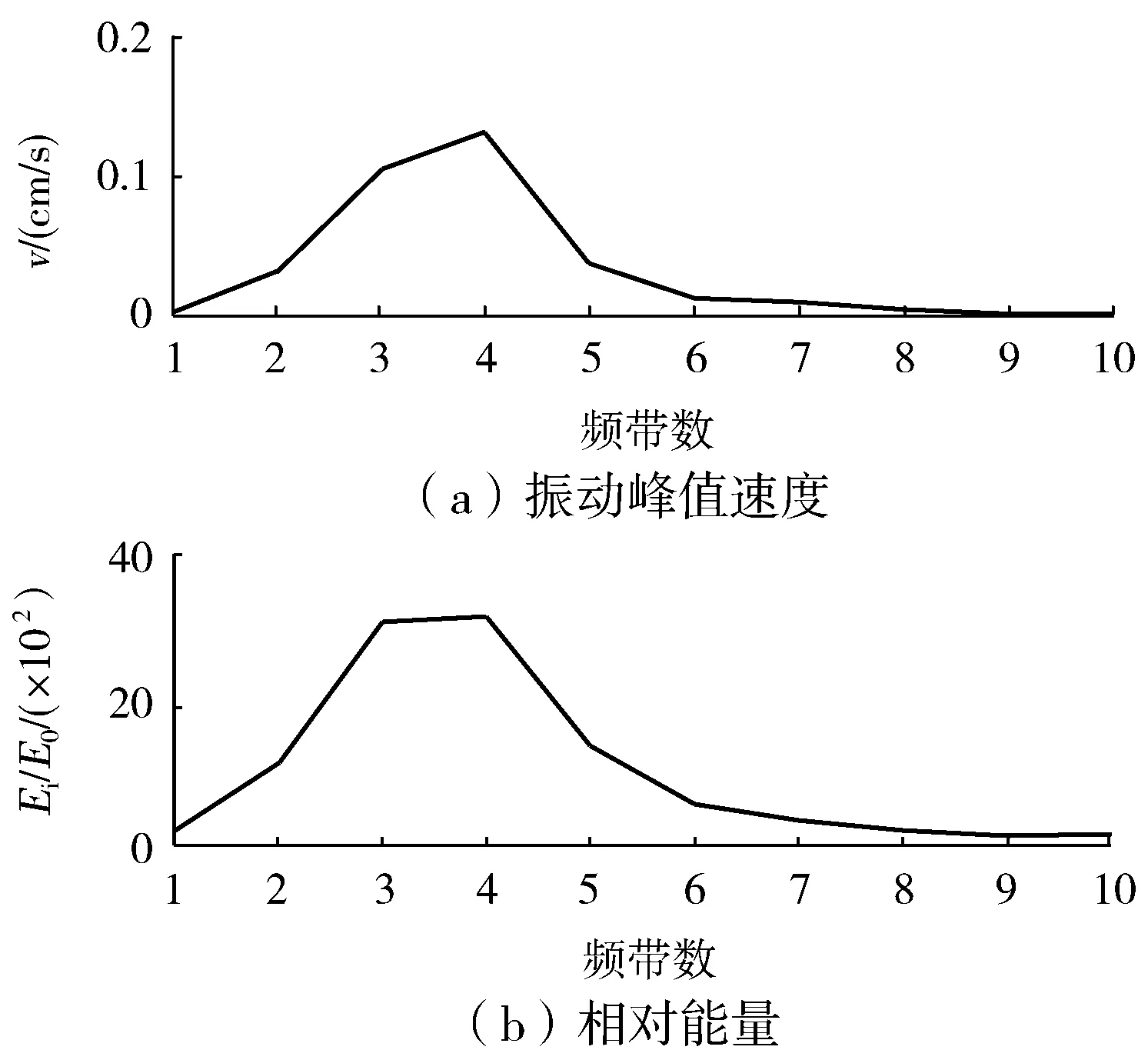
图4 水平切向不同频带下质点振动峰值速度和相对能量分布图Fig.4 Different frequency bands peak particle velocity and relative energy distribution of horizontal tangential
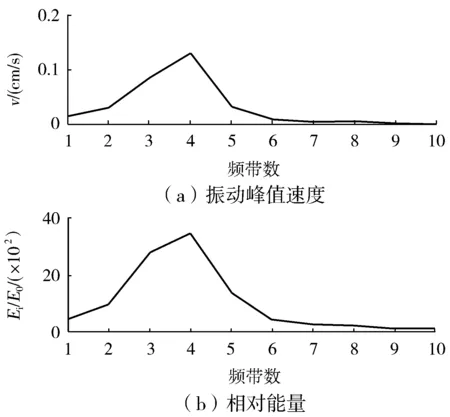
图5 垂直方向不同频带下质点振动峰值速度和相对能量分布图Fig.5 Different frequency bands peak particle velocity and relative energy distribution of vertical
(4)低频部分爆破振动波能量较高,高频部分爆破振动波能量极少。这是因为高频部分能量持续时间短,衰减极快,如表2所示。
(5)逐孔起爆三向振动信号在不同频带能量分布不同,各向能量主要集中在250 Hz以内,250 Hz以后能量基本消失。
4 结 语
质点峰值速度、频率特性、振动持时作为评价爆破振动安全的三要素,人们往往忽略后2个因素的影响。对某露天矿距爆源140 m处振动数据监测,并利用小波理论对其分频能量分布进行分析,爆破振动频带能量主要集中在15 Hz以上,由于周围建(构)筑物固有频率较低,因此,此次爆破共振对建(构)筑物的影响较小。同时得到以下结论:逐孔起爆频带能量的最大值与质点峰值振速基本处于相同位置,总体上成正比例关系,但个别频带能量最大值并不处于峰值振速位置;逐孔起爆三向振动信号在不同频带能量分布不同,各向能量主要集中在250 Hz以内,250 Hz以后能量基本消失。
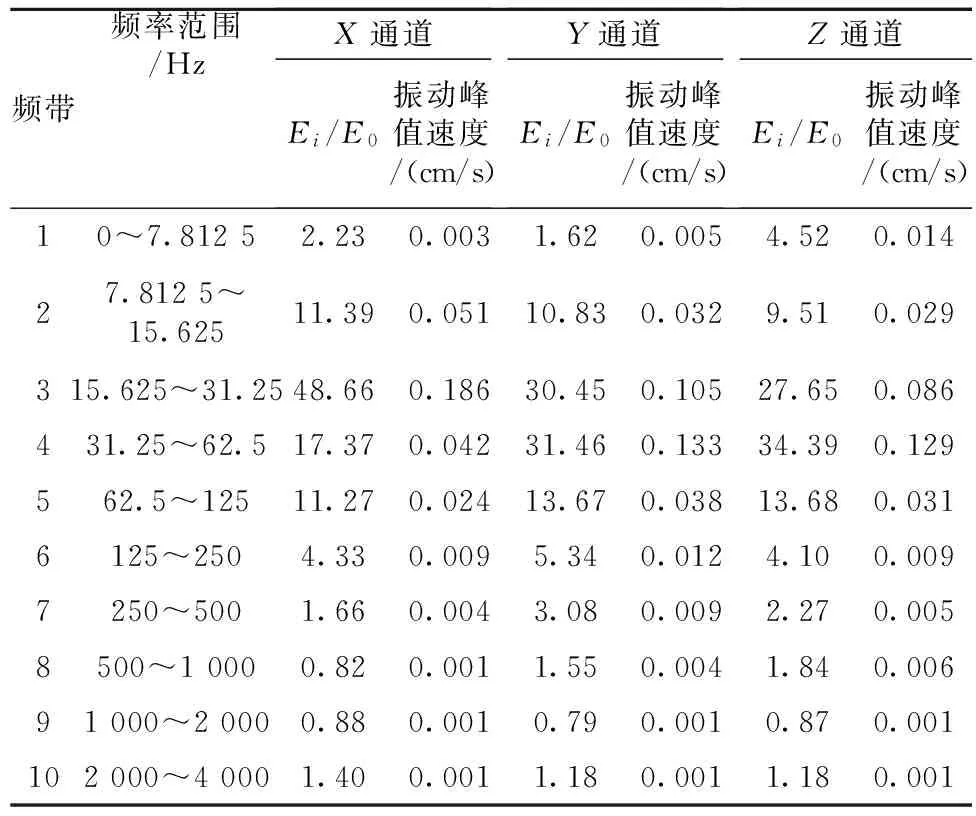
表2 爆破振动信号频带能量分布数据Table 2 Blasting vibration signal data for each band
[1] 赵明生,张建华,易长平.基于小波分解的爆破振动信号RSPW VD二次型时频分析[J].振动与冲击,2011,2(30):44-47. Zhao Mingsheng,Zhang Jianhua,Yi Changping.Blasting vibration signal PSPWVD quadratic time-frequency analysis based on wavelet decomposition[J].Journal of Vibration and Shock,2011,2(30):44-47.
[2] 何 军,于亚伦,梁文基.爆破震动信号的小波分析[J].岩土工程学报,1998,20(1):47-50. He Jun,Yu Yalun,Liang Wenji.Wavelet analysis for blasting seismic signals[J].Chinese Journal of Geotechnical Engineering,1998,20(1):47-50.
[3] 晏俊伟,龙 源,方 向,等.基于小波变换的爆破振动信号能量分布特征分析[J].爆炸与冲击,2007,27(5):405-410. Yan Junwei,Long Yuan,Fang Xiang,et al.Analysis of the features of energy distribution for blasting seismic wave based on wavelet transform[J].Explosion and Shock Waves,2007,27(5):405-410.
[4] 徐守时.信号与系统[M].合肥:中国科学技术大学出版社,1999:2-12. Xu Shoushi.Signals and Systems[M].Hefei: University of Science & Technology China Press,1999:2-12.
[5] 凌同华,李夕兵.爆破振动信号不同频带的能量分布规律[J].中南大学学报:自然科学版,2004,34(2):310-315. Ling Tonghua,Li Xibing.Laws of energy distribution in different frequency bands for blast vibration signals[J].Journal of Central South University:Science and Technology edition,2004,34(2):310-315.
[6] 王更峰,汤庆荣.岩石声发射信号能量的小波包分析[J].工程勘察,2007(8):69-72. Wang Gengfeng,Tang Qingrong.Wavelet packet analysis on signal energy of rock acoustic emission[J].Geotechnical Investigation & Surveying,2007(8):69-72.
[7] 张耀平,曹 平,高赛红.爆破振动信号的小波包分解及各频段的能量分布特征[J].金属矿山,2007(11):42-47. Zhang Yaoping,Cao Ping,Gao Saihong.Wavelet packet decomposition of blasting vibration signals and energy distribution characteristics of frequency bands[J].Metal Mine,2007(11):42-47.
[8] 蒋丽丽,林从谋,陈泽观,等.岩石高边坡爆破振动传播规律小波包分析[J].有色金属:矿山部分,2009,61(2):43-46. Jiang Lili,Lin Congmou,Chen Zeguan,et al.Wavelet Packet Analysis of Vibration Caused by High Rock Slope Blasting[J].Nonferrous Metals:Mine Section,2009,61(2):43-46.
[9] Jan F A.River flow forecasting using wavelet and cross-wavelet transform models[J].Hydrological Process,2008,22:4877-4891.
[10] 张智宇,栾龙发,殷志强,等.起爆方式对台阶爆破振频能量分布的影响[J].爆破,2008,25(2):21-25. Zhang Zhiyu,Luan Longfa,Yin Zhiqiang,et al.Effects of detonation ways on energy distribution for different frequency bands of bench blasting[J].Blasting,2008,25(2):21-25.
(责任编辑 徐志宏)
Analysis on Different Frequency-band Energy of Blasting Vibration Signal based on Wavelet Transform
Wang Tao1Xia Anxiong2Liao Xinxu1
(1.GuangdongHongdaBlastingCo.,Ltd.,Guangzhou510623,China;2.SchoolofResourcesandEnvironmentalEngineering,WuhanUniversityofTechnology,Wuhan430070,China)
In view of non-stationary characteristics of short-time blasting vibration and quick abrupt change and the signal spread in three directions,and combining with the measured data of hole-by hole blasting in an open pit mine,the energy distribution of vibration signal in axial,radial,vertical direction at a certain point was analyzed by adopting the wavelet analysis method.The results showed that maximum frequency-band energy and peak particle velocity were basically in the same position with a proportional relationship,but sometimes some individual maximum frequency band energy was different.Three-directional vibration signals of hole-by-hole blasting were differently distributed into different frequency bands.The energy at each direction mainly concentrates within 250 Hz,and will disappear beyond 250 Hz; The blasting resonance less impacted on buildings,because the building's natural frequency at surrounding is lower and the vibrating energy at 140 m away from explosion source mainly concentrates in 15 Hz or more.The result provides a new approach for safety evaluation under blasting vibration conditions.
Hole-by-hole blasting,Vibration monitoring,Vibration signal,Wavelet transform,Energy distribution
2013-11-17
王 涛(1988—),男,硕士研究生。
TD235.1+4
A
1001-1250(2014)-03-052-04

