一种交通枢纽流线优化设计的方法
胡春平,毛保华,朱宇婷,甘恬甜,张 政
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京100044)
一种交通枢纽流线优化设计的方法
胡春平,毛保华*,朱宇婷,甘恬甜,张 政
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京100044)
本文充分分析了熟悉型和陌生型两类乘客的路径选择行为,结合枢纽网络的特有属性,建立了枢纽流线优化模型.从枢纽管理者的角度出发,通过调整枢纽通道的分配方案,间接影响乘客的路径选择行为,从而降低系统总费用.结合问题特点,采用Frank-Wolfe算法和Logit模型分别计算两类乘客的路径选择概率.在此基础上,采用遗传算法对模型进行求解.最后,通过算例对模型和算法进行了验证.
城市交通;交通枢纽;流线优化;优化模型;路径选择
1 引 言
城市客运枢纽作为公共交通体系的重要组成部分,起到平衡和衔接城市客运交通体系内各子系统的重要作用,其运行效率的好坏,将直接影响综合客运网络的整体效率和服务水平.
国内外针对枢纽流线优化问题已有较多研究.漆凯基于最大熵原理,构建乘客流线优化模型[1];胡春平等将城市道路交通网络的配流方法应用在枢纽流线设计中,建立了基于客流分配的枢纽流线优化模型[2];Jiang等从乘客路径选择的角度出发,采用交叉熵计算方法对旅客流线进行优化[3].上述研究虽然在一定程度上解决了枢纽流线优化问题,但随着枢纽规模的不断扩大,“枢纽站内的旅客从一个相同的出发地到相同目的地之间仅有一条确定的路径”的基本假设的局限性逐渐凸显.因此,有必要深入研究枢纽内乘客的路径选择行为,通过合理分配通道资源,优化枢纽内旅客走行流线,提高枢纽运行效率.
目前,交通网络资源配置优化问题主要运用于道路交通领域.Wolshon等讨论了飓风疏散时高速公路上的车道单行预案[4];Kim等利用单向交通组织方法研究多源点疏散网络优化问题[5];严新平等研究了大型活动后的交通疏导问题,以总疏散时间最短为目标,建立了车道单行优化问题的双层规划模型[6];Xie等运用单向交通组织方法研究快速疏散问题,以总疏散时间最短为目标建立了双层规划模型[7].然而,道路交通网络与枢纽交通网络存在一定的差异,前者主要服务于车辆,其在道路上的运动相对规则,而枢纽交通网络主要服务于乘客,其运动的主观性、随机性较强.因此,上述研究并不完全适用于枢纽交通网络.
本文将出行者按照对交通网络的知晓程度分为熟悉型和陌生型两类,以系统总费用最小为目标,建立枢纽旅客流线优化模型,并设计了相应的求解算法.最后,以某一枢纽站为例,对模型及算法进行了验证.
2 乘客路径选择行为
根据乘客对交通网络熟悉程度的不同,将乘客分为熟悉型和陌生型两类.熟悉型乘客主要是指对枢纽网络结构、出行路径等非常熟悉,具有长期出行经验的出行者;陌生型乘客主要是指对枢纽网络并不熟悉,第一次或很少进入该网络的出行者.
2.1 熟悉型乘客的路径选择行为
熟悉型乘客经过长期的经验积累,对OD对各可选路径的费用进行评估,选择个体认为的最优路径.其出行阻抗一般采用广义旅行时间函数,主要包括区段运行时间、节点通过时间等,乘客选择OD对rs间第k条路径的阻抗函数为
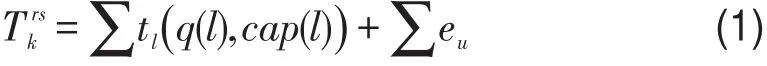
式中 q(l)表示通道l的流量;cap(l)表示通道l的理论通行能力;tl(·)表示通道l的通行时间,其与通道流量、通道通过能力相关;eu表示节点u的延误时间.
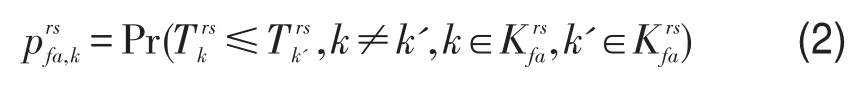
2.2 陌生型乘客的路径选择行为
陌生型乘客在枢纽内的走行次数有限,无法形成长期的经验积累,难以预先估计各条路径的广义费用.因此,这类乘客一般根据决策部门提供的示意图完成路径选择.其选择OD对rs间第k条路径的阻抗为

式中 Hl表示乘客通过缩略图对通道l的估计通过时间.
则陌生型乘客选择OD对rs间第k条路径的概率 prsfu,k为
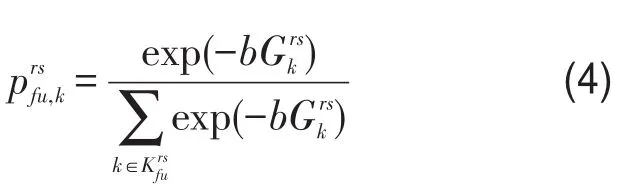
3 模型及算法
3.1 模 型
枢纽站内的网络结构可以用有向图G=(V⋃U,L)表示.V为起讫点集合,U为中间节点集合,L为通道集合.其中,双向通道集合为L,单向通道集合L~=L-L .每个双向道路由两条方向相反的通道组成,记正向通道为l,反向通道为l′.起讫点间rs的交通需求为Qrs.通道单位宽度通过能力为C0,通道具有单位宽度的个数为M(l).X(l)为优化变量,表示通道l分配到的单位宽度数.
假设决策者会提前发布枢纽网络示意图,每位出行者对通道的禁行情况都有一定的了解,则以系统总费用最优为目标,可构造相应的枢纽流线优化模型如下

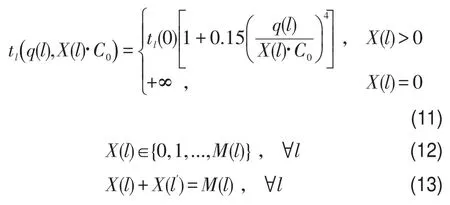
在约束条件中,式(6)是各路径流量和总流量的平衡约束;式(7)决定了各条路径上两类乘客的流量与总流量的关系;式(8)、式(9)分别决定了各条路径上陌生型和熟悉型乘客的流量;式(10)决定了各节点的流量;式(11)给出了通道l的实际通过时间;式(12)确定了决策变量X(l)的取值范围;式(13)决定了通道双方向宽度之和不能超过总宽度.
3.2 求解算法
本文采用遗传算法对模型进行求解,基本步骤如下:
Step1初始化.给定种群规模N,交叉概率pc,变异概率pm,最大进化代数M.取式(5)为适应度函数,随机生成初始可行解X1,置进化代数m=1.
Step2针对每个个体,先采用Logit配流方法分配陌生型客流,再采用Frank-Wolfe算法分配熟悉型客流,计算每个个体的适应度函数.
Step3根据交叉概率pc,执行交叉操作.
Step4根据变异概率pm,执行变异操作,得到新种群Xm+1.
Step5若满足终止准则m+1=M,算法结束;否则,令m=m+1,转Step2.
4 算例计算与分析
本文采用一个简单的枢纽网络对模型及算法进行验证,枢纽网络如图1所示.表1为网络基本参数,表2为某时段OD客流量.
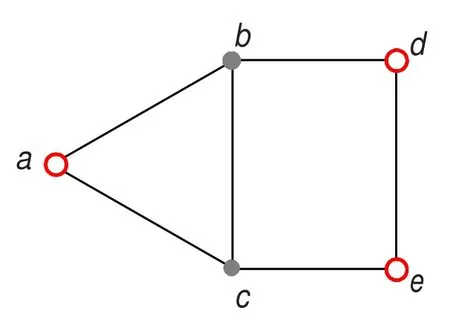
图1 枢纽交通网络图Fig.1 A hub network
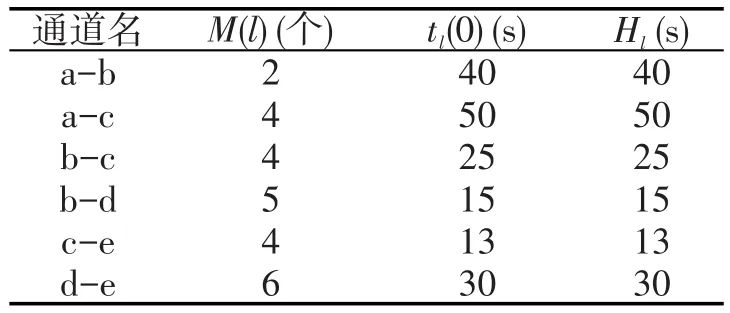
表1 网络基本信息Table.1 Basic circumstance of the network

表2 某时段OD流量(p/h)Table.2 Passenger flow volume for each OD pair
假设两类乘客各占一半(ωfa=ωfu=0.5),乘客通过节点的平均延误时间为5 s,通道单位宽度通过能力C0=2 355 p/h.通过Matlab软件进行编程,求得枢纽通道分配结果如表3所示.可以发现:优化后的枢纽交通网络存在2条单向通道及4条双向通道,且通道各方向饱和度相对均匀,平均路段饱和度为52.52%.
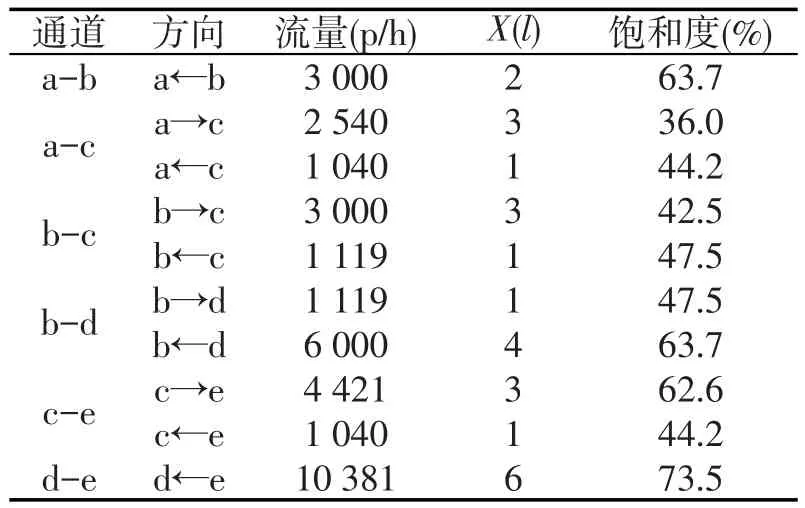
表3 枢纽通道分配结果Table.3 Hub network optimization results
表3得到的通道分配方案对应的旅客流线优化结果如图2所示.
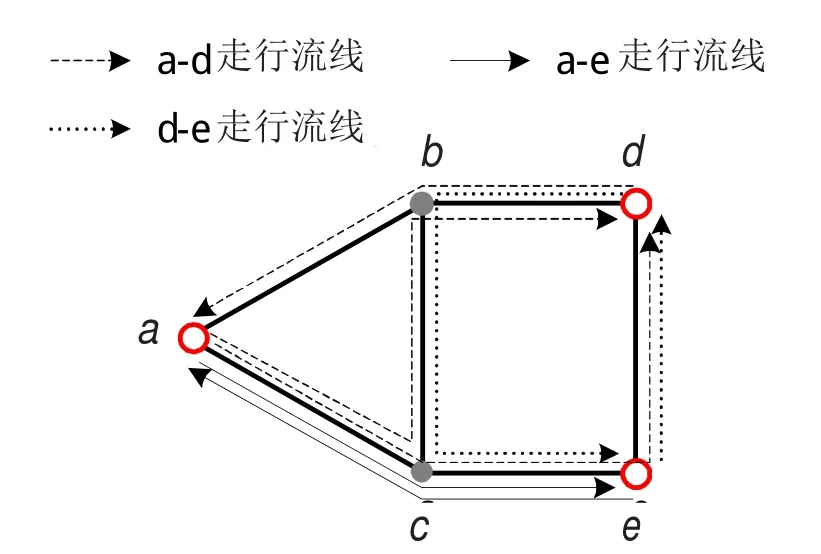
图2 旅客流线优化结果Fig.2 The optimization result of passenger flow routing
图3为不同乘客比例下单向通道比例的变化情况.由图可以看出,随着熟悉型乘客比例的不断增加,单向通道的比例总体呈下降趋势.当熟悉型乘客的比例为0时,单向通道比例为100%;当熟悉型乘客的比例增至50%时,单向通道比例降为33.33%;当熟悉型乘客比例增至100%时,单向道比例降至0.结果表明,出行乘客的类型对枢纽通道分配结果的影响较大,在建立枢纽旅客流线优化模型时,有必要考虑不同类型乘客的选择行为.
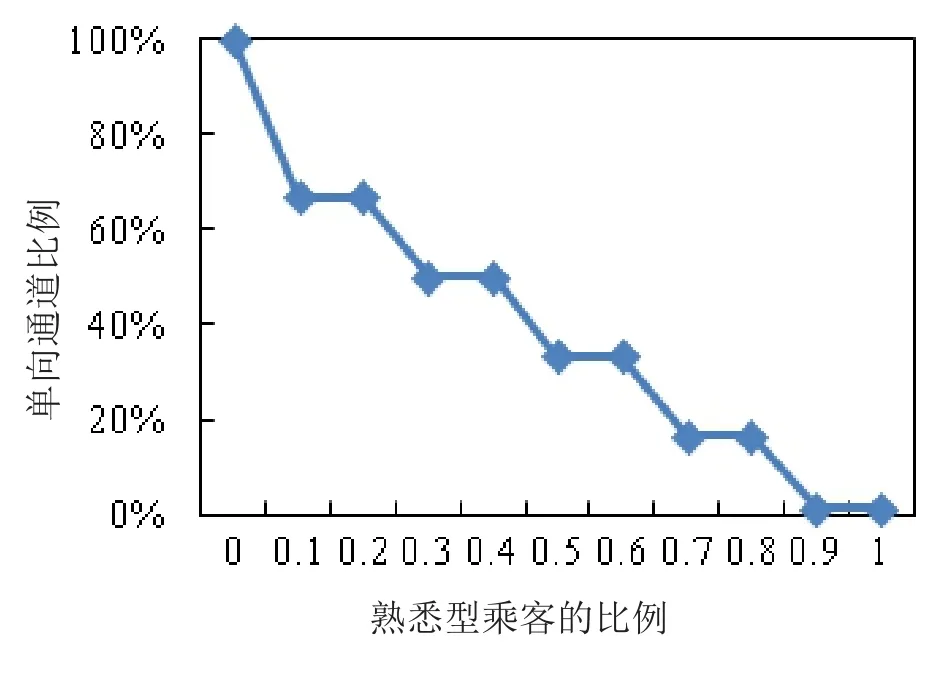
图3 不同乘客比例情况下单向通道比例的变化情况Fig.3 The change of one-way channels with different passengers composition
[1]漆凯.基于最大熵原理的地铁换乘站乘客流线优化模型[J].物流技术,2011,30(10):87-90.[QI K.Model of metro interchange station passenger line optimization based on maximum entropy principle[J].Logistics Tech⁃nology,2011,30(10):87-90.]
[2]胡春平,毛保华,朱宇婷.综合客运枢纽旅客全过程流线优化模型[J].交通运输系统工程与信息,2012,03 (12):159-164,186.[HU C P,MAO B H,ZHU Y T. Streamline design and optimization for whole process of passenger transfer in integrated transportation hubs[J]. Journal Transportation Systems Engineering and Infor⁃mation Technology,2012,03(12):159-164,186.]
[3]Jiang Y,Zhang X C,Gan T T.A cross-entropy method for solving passenger flow routing problem[J].Advanced Materials Research,2013,756:3617-3621.
[4]Wolshon B,Urbina E,Levitan M.National review of hurricane evacuation plans and policies:a comparison and contrast of state practices[J].Transportation Re⁃search Part A,2003,37(03):257-275.
[5]Kim S,Shekhar S,Min M.Contra flow transportation net⁃work reconfiguration for evacuation route planning[J]. IEEE Transaction on Knowledge and Data Engineering, 2008,20(8):1115-1129.
[6]严新平,吕能超,刘正林,等.大型活动后车道单行优化的双层规划[J].西南交通大学学报,2009,44(1): 112-117.[YAN X P,LU N C,LIU Z L,et al.Bi-level programming for optimization of contraflow lanes after massive activities[J].Journal of Southwest Jiaotong Uni⁃versity,2008,27(3):89-92.]
[7]Xie C,Lin D Y,Travis Waller S.A dynamic evacuation network optimization problem with lane reversal and crossing elimination strategies[J].Transportation Re⁃search Part E:Logistics and Transportation Review, 2010,46(3):295-316.
5 研究结论
本文提出了考虑出行者类别的枢纽旅客流线优化模型.模型在描述枢纽管理者对枢纽管理的同时,还考虑了乘客的路径选择行为.分别采用Logit模型和F-W算法对陌生型乘客和熟悉型乘客进行配流.算例结果表明,该方法可用于优化不同乘客比例下的枢纽流线.但是,该优化模型未能囊括实际生活中的各类人群,这将成为下一步的研究重点.
Optimization Method of Passenger Flow Routing Problem
HU Chun-ping,MAO Bao-hua,ZHU Yu-ting,GAN Tian-tian,ZHANG Zheng
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology,Beijing 100044,China)
This paper focuses on different route choice behaviors and characteristics for two types of passengers:the familiar type and unfamiliar type.It develops an optimization model for passenger flow routing with consideration of specific attributes of hub network.This study adjusts distribution schemes of the channel,which has certain impacts on passenger’s route choice behaviors.It then minimizes the system cost from the perspective of hub manager.Considering the significant feature of the problem,this study also estimates the probability of each route selected by different types based on the Frank-Wolfe method and Logit model. Moreover,a genetic algorithm is used to solve the problem.Finally,a simple case study illustrates the effectiveness of the proposed method.
urban traffic;passenger hub;network design;optimization model;route choice
1009-6744(2014)02-0158-04
V211,U491.1
A
2013-10-17
2013-12-29录用日期:2014-01-11
国家自然科学基金(71131001);国家自然科学青年基金项目(71201006).
胡春平(1975-),男,湖南涟源人,博士生.*通讯作者:bhmao@china.com

