Levitin-Polyak Well-posedness of Hemivariational Inequalities in Banach Spaces
QIU Dan
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
In 1966,Tykhonov[1]first gave the well-posedness of a minimization problem,which has been known as Tykhonov well-posedness.Roughly speaking,the Tykhonov well-posedness of a minimization problem means the existence and uniqueness of minimizers,and the convergence of every minimizing sequence toward the unique minimizer.In many practical situations,there are more than one minimizers for a minimization problem.In this case,the concept of Tykhonov well-posedness in the generalized sense was introduced,which means the existence of minimizers and the convergence of some subsequence of every minimizing sequence toward a minimizer.Clearly,the concept of well-posedness is motivated by the numerical methods producing optimizing sequences.Because of its importance in optimization problems,various concepts of well-posedness have been introduced and studied for minimization problems in past decades.For details,we refer the readers to[2-4]and the references therein.
The Tykhonov well-posedness of a constrained minimization problem requires that every minimizing sequence should lie in the constraint set.In many practical situations,the minimizing sequence produced by a numerical optimization method usually fails to be feasible but gets closer and closer to the constraint set.Such a sequence is called a generalized minimizing sequence for constrained minimization problems.To take care of such a case,Levitin and Polyak[5]strengthened the concept of Tykhnov well-posedness by requiring the existence and uniqueness of minimizer,and the convergence of every generalized minimizing sequence toward the unique minimizer,which has been known as Levitin and Polyak(for short,LP)wellposedness.There are a very large number of results concerned with Tykhonov well-posedness,LP wellposedness and their generalizations for minimization problems.For details,we refer the readers to[1-3,5-7].
On the other hand,Hu and Fang[8]considered the Levitin-Polyak well-posedness of a general variational inequality in Rn.They derived some characterizations of the Levitin-Polyak well-posedness by considering the size of Levitin-Polyak approximating solution sets of general variational inequalities.They also proved that the Levitin-Polyak well-posedness of a general variational inequality is closely related to the Levitin-Polyak well-posedness of a minimization problem and a fixed point problem.Finally,they showed that under suitable conditions,the Levitin-Polyak well-posedness of a general variational inequality is equivalent to the uniqueness and existence of its solutions.
As an important and useful generalization of variational inequality,hemivariational inequality was first introduced in order to formulate variational principles connected to energy functions,which are neither convex nor smooth,and investigated by Panagiotopoulos[9]by using the mathematical concept of the generalized gradient of Clarke for nonconvex and nondifferentiable functions[10].The hemivariational inequalities have been proved very efficient to describe a variety of mechanical problems(see,for example[11-13]).So,in recent years all kinds of hemivariational inequalities have been studied[14-17].However,there are very few researchers extending the Levitin-Polyak well posedness to hemivariational inequalities.
Motivated and inspired by the research work going on this field,we extend the notion of Levitin-Polyak well-posedness to a hemi-variational inequality in Banach spaces.We establish some metric characterizations for the Levitin-polyak well-posed hemivariational inequality.We also investigate the relationship between the Levitin-Polyak well-posedness of HVI(A,f,j,K)and the Levitin-Polyak well-posedness of optimization problem which includes the gap function of hemivariational inequality.
1 Preliminaries
LetVbe a real reflexive Banach space with its dual spaceV*,andKbe a nonempty,closed and convex subset ofV,fbe a point inV*.LetT:V→Lp(Ω,Rm) be a linear and continuous mapping,where 1≤p<∞,m≥1,and Ω is a bounded open set in Rn,n≥1.LetA:V→V*be a mapping,andj=j(x,y):Ω × Rm→R is a Caratheodory function which is locally Lipschitz with respect to the second variabley∈Rmand satisfies the following assumption:there existandh2∈L∞(Ω,Rm)such that for almostx∈Ω,and anyy∈Rm,z∈∂j(x,y),

where ∂j(x,y)denotes the Clarke generalized gradient of the locally Lipschitz functionalj(x,·)at the pointy∈Rm.Denote byTu=^u,u∈V,we consider the following hemivariational inequality associated with(A,f,j,K).

We denotejo(x,y;h)the Clarke generalized directional derivative of the locally Lipschitz functionalj(x,·)at the pointy∈Rmwith respect to the directionh∈Rm,wherex∈Ω and ∂j(x,y)denote the Clarke generalized gradient aty∈Rm,that is
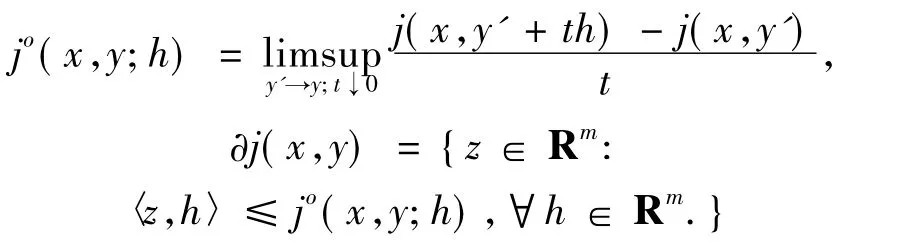
Remark 1.1Whenf=0 andj=0,HVI(A,f,j,K)reduces to the classical variational inequality,VI:findu∈Ks.t.〈Au,v-u〉≥0,∀v∈K.
Definition 1.1A nonempty mappingA:V→V*is said to be monotone if for allu,v∈V,

Definition 1.2A nonempty mappingA:V→V*is said to demicontinuous if for any sequence{un}⊂Vconverging tou,one has{Aun}weakly converges toAu.
Definition 1.3A nonempty set-valued mappingAbetween two separated spacesXandYis said to be upper semicontinuous(USC)atx∈Xif for every open setV∈Ywhich includesA(x),there exists a neighbourhoodU⊂Xsuch thatA(U)⊂V.
Lemma 1.1LetV1,V2are nonempty subsets ofV,then the mappingV1×V2→R defined by
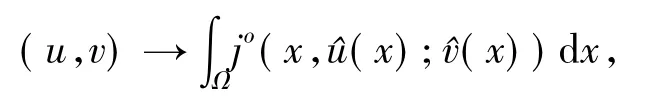
is upper semicontinuous,whereu∈V1,v∈V2.
Lemma 1.2Letjo(x,y;h)be the Clarke generalized directional derivative of the locally Lipschitz functionalj(x,·)at the pointy∈Rmwith respect to the directionh∈Rm.Then the functionh→jo(x,y;h)is finite,positive homogeneous and subadditive.
Proposition 1.1LetKbe a nonempty,closed and convex subset ofV,A:V→V*be a monotone and demicontinuous mapping.Then for a givenu∈K,the following statements are equivalent:
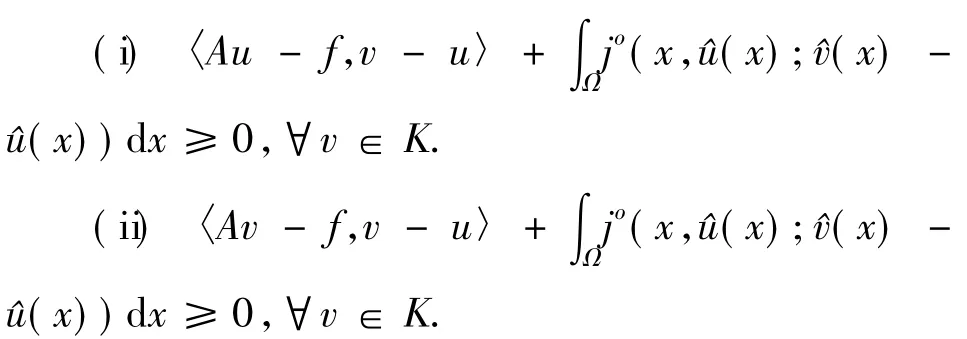
ProofSuppose that(i)holds,we haveu∈Kand
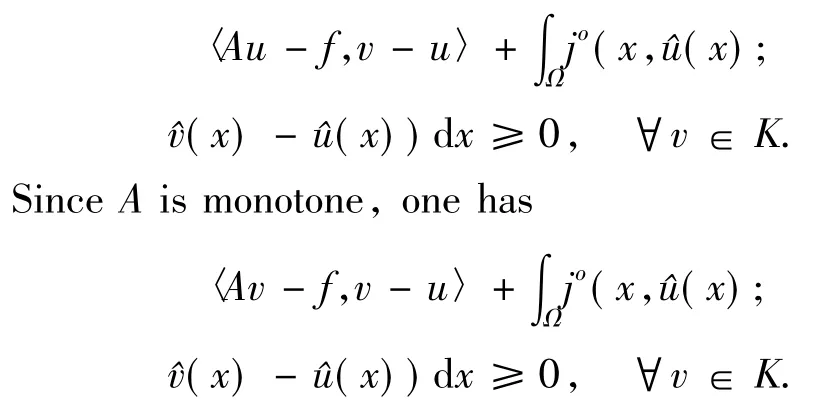
Conversely,suppose that the last inequality is valid,given anyvt=u+t(v-u)for allt∈(0,1),it is obvious thatvt∈KsinceKis convex.Then replacingvbyvtint the left-hand side of the last inequality,one has
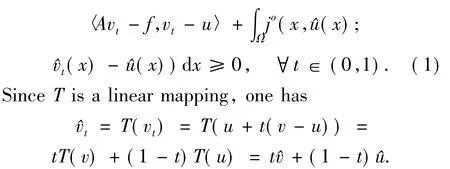
By Lemma 1.2,one hasjo(x,(x);·)is positive homogeneous,this fact,together with(1)implies that
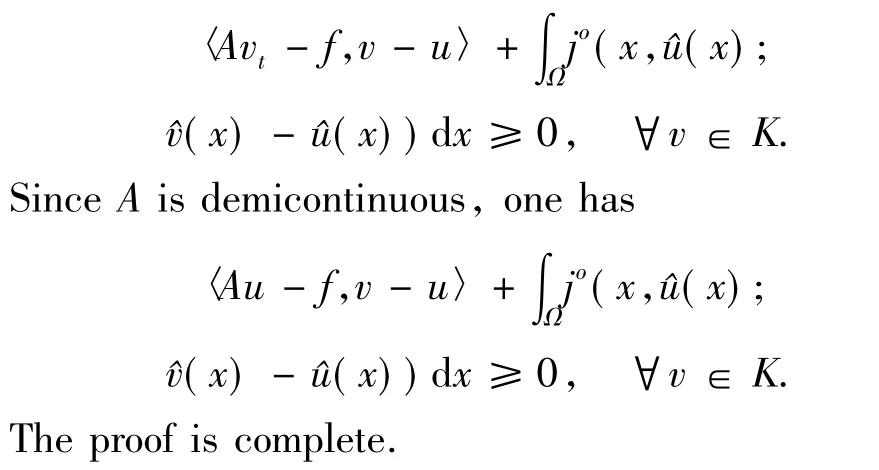
2 Levitin-Polyak well-posedness and metric characterization
In this section,we give some metric characterization for the Levitin-Polyak well-posednessfor HVI(A,f,j,K).letA,f,j,Kbe defined as in the previous section.
Definition 2.1A sequence{un}⊂Vis said to be an LP approximating sequence for HVI(A,f,j,K)if there existwn∈Vwithwn→0 such thatun+wn∈K,for alln∈N,and there exists 0<∈n→0 such that

Definition 2.2We say that HVI(A,f,j,K)is LP well-posed if HVI(A,f,j,K)has a unique solution and every LP approximating sequence converges to the unique solution.
Definition 2.3We say that HVI(A,f,j,K)is LP well-posed in the generalized sense if HVI(A,f,j,K)has nonempty solution setSand every LP approximating sequence has a subsequence which converges to some point ofS.
To derive the metric characterizations of LP wellposedness,we consider the following LP approximating solution set of HVI(A,f,j,K):

Now we give a metric characterization of LP well-posedness for HVI(A,f,j,K).
Theorem 2.1LetA:V→V*be a monotone and demicontinuous mapping.Then HVI(A,f,j,K)is LP well-posed if and only if

ProofSuppose that HVI(A,f,j,K)is LP wellposed.Then HVI(A,f,j,K)has a unique solution which belongs to Ω(∈)for all∈>0.If diamΩ(∈)→0 as∈→0,then there exist a constantl>0 and 0 < ∈n→0 andsuch that
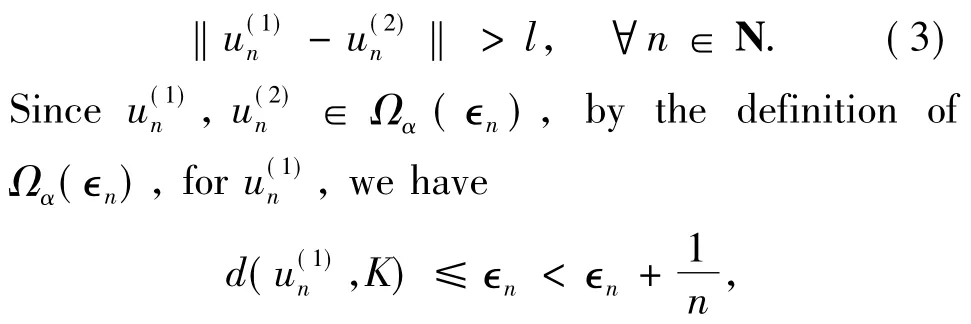

Conversely,suppose that(2)holds.Let{un}⊂Vbe an LP approximating sequence for HVI(A,f,j,K).Then there existswn∈Vwithwn→0 such thatun+wn∈K,and there exists 0 < ∈n'→0 such that
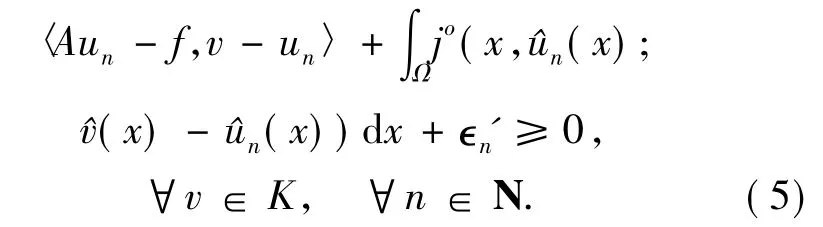
Sinceun+wn∈K,then there existsn∈Ksuch thatun+wn=n.It is easy to seed(un,K)≤‖un-n‖= ‖wn‖→0.Set∈n=max{∈'n,‖wn‖},one hasun∈Ωα(∈n).It follows from(2)that{un}is a Cauchy sequence and so it converges to a pointu∈K.SinceAis monotone,By Lemma 1.1,we have for anyv∈K,

From Proposition 2.1,usolves HVI(A,f,j,K).To complete the proof,we need to prove HVI(A,f,j,K)has a unique solution.Assume by contradiction that HVI(A,f,j,K)has two distinct solutionsu1andu2.Then it is easy to see thatu1,u2∈Ω(∈)for all∈>0,and

a contradiction to(2).The proof is complete.
Theorem 2.2LetA:X→X*be a continuous mapping.Then HVI(A,f,j,K)is LP well-posed in the generalized sense if and only if

ProofWe suppose that HVI(A,f,j,K)is LP well-posed in the generalized sense.LetSbe the solution set of HVI(A,f,j,K).ThenSis nonempty and compact.Indeed,let{un}⊂Sis an LP approximating sequence for HVI(A,f,j,K).Since HVI(A,f,j,K)is LP well-posed in the generalized sense,{un}has a subsequence which converges to some point ofS.Thus,Sis compact.It is obvious that Ω(∈)⊃S≠Øfor all∈>0.Now we show that

Indeed,ife(Ωα(∈),S)0 as∈→0.then there existl>0 and{∈n}⊂R+with ∈n→0,andun∈Ωα(∈n)such that

whereB(0,l)is the closed ball centered at 0 with radiusl.By the definition of Ωα(∈n),we knowd(un,K),and

Then there existsn∈Ksuch that.Letwn=n-xn,then we havewn+un∈Kwithwn→0.This implies that{un}is an LP approximating sequence for HVI(A,f,j,K).Since HVI(A,f,j,K)is LP well-posed in the generalized sense,there exists a subsequence{unk}of{un}which converges to some point ofS.This contradicts(7)and so

Conversely,we suppose that(6)holds.First,we show that Ω(∈)is closed.Let{un}⊂Ω(∈)andun→u.Then we haved(un,K)≤∈and

It is easy to seed(u,K)≤∈.SinceAis continuous,this fact together with Lemma 1.1 implies that

This implies thatu∈Ω(∈)and so Ω(∈)is nonempty closed for all∈>0.
Observe that
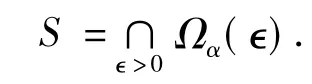
Sinceu(Ωα(∈))→0,the Theorem in page 412 of[18]can be applied and one concludes thatSis nonempty and compact with

Let{un'}⊂Vbe an LP approximating sequence for HVI(A,f,j,K).Then there existswn∈Vwithwn→0 such thatun'+wn∈K,and there exists 0 < ∈'n→0 such that

Sinceun'+wn∈K,there existsn'∈Ksuch thatun'+wn=n'.It follows that

Set∈n=max{‖wn‖,∈'n},we getun'∈Ωα(∈n).It follows from(6)and the definition of Ωα(∈n)that
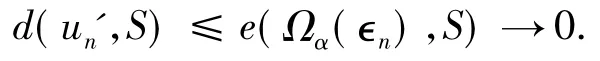
SinceSis compact,there existspn∈Ssuch that

Again from the compactness ofS,there exists a subsequence{pnk}of{pn}which converges strongly to∈S.Hence the corresponding subsequence{u'nk}of{un'}converges strongly to∈S.Thus,HVI(A,f,j,K)is LP well-posed in the generalized sense.
Theorem 2.3HVI(A,f,j,K)is LP well-posed in the generalized sense if and only if the solution setSof HVI(A,f,j,K)is compact and the set-valued mapping from R toVdefined by
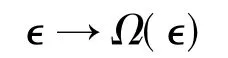
is upper semicontinuous at∈=0,where∈≥0.
ProofAssume that HVI(A,f,j,K)is LP wellposed in the generalized sense.It follows from the similar argument of Theorem 2.2 thatSis nonempty compact.Noticing thatS=Ω(0).Suppose to the contrary,for some open setUand 0 < ∈n→0 such that

Then there exists an LP approximating sequence for HVI(A,f,j,K)without cluster points insideS,a contradiction.
Conversely,let{un}be an LP approximating sequence for HVI(A,f,j,K),then there existswn∈Vwithwn→0 such thatun+wn∈K,and there exists 0< ∈n'→0 such that
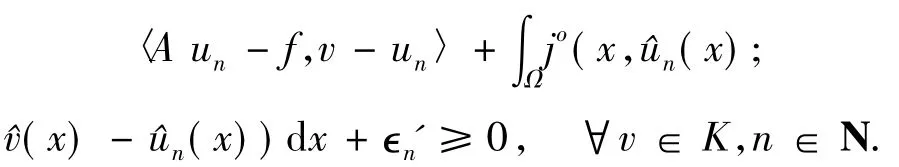
Sinceun+wn∈K,one hasd(un,K)≤‖wn‖→0.Set∈=max{‖wn‖,∈n'},we haveun∈Ω(∈n)with∈n→0.By the compactness ofSand ∈→Ω(∈)is upper semicontinuous at∈=0,we have{un}has a subsequence{unk}converging to some point ofS.This yields that HVI(A,f,j,K)is LP well-posed in the generalized sense.
Lemma 2.1LetKbe a compact and convex subset ofV.If the mappingA:V→V*is demicontinuous,then HVI(A,f,j,K)admits a solution.
Theorem 2.4LetA:V→V*be a monotone and demicontinuous mapping.If for any∈>0,Ω(∈)≠Øand there exists some δ> 0 such that Ω( δ)is compact,then HVI(A,f,j,K)has least a solution.
ProofFor any∈>0,Ω(∈)≠Ø.Let{un}be a sequence such that.Since there exists some δ> 0 such that Ω( δ)is compact.Fornsufficiently large,we haveand so{un}⊂Ω(δ).By the compactness of Ω(δ),there exists a subsequence{unk}of{un}andu∈Ω(δ)such thatunk→u.Since,we have,and
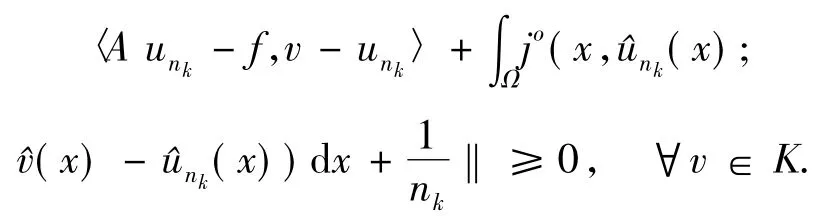
It is easy to seeu∈K.SinceAis monotone,from the last inequality,we have
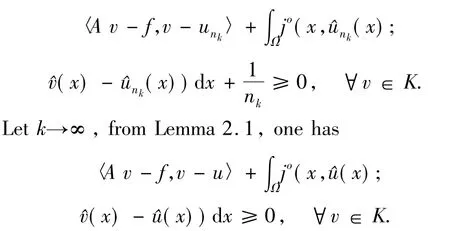
Given anyvt=u+t(v-u)for allt∈(0,1),it is obvious thatvt∈KsinceKis convex.Then replacingvbyvtin the left-hand side of the last inequality,one has
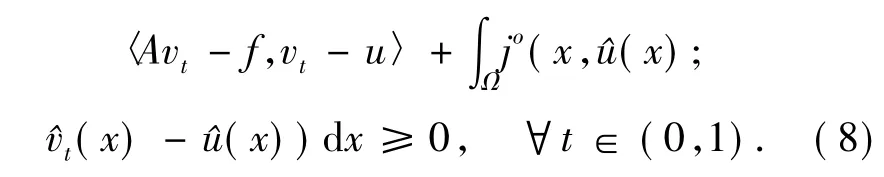
SinceTis a linear mapping,it follows from Lemma 1.2 that
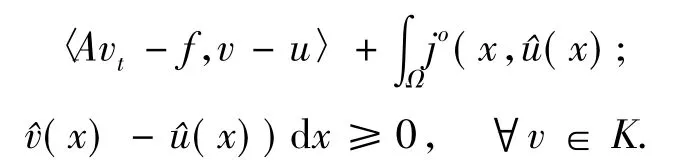
SinceAis demicontinuous,one has
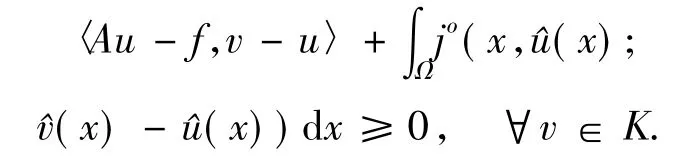
This shows thatusolves HVI(A,f,j,K).
3 Links with Levitin-Polyak well-posedness of gap function
In this section,we will investigate the relationship between the LP well-posedness of HVI(A,f,j,K)and the LP well-posedness of the gap function,we first consider the following minimization problem:

we denoteV0andzbe the optimal set and optimal value of(P)respectively.In what follows we recall some concepts.
Definition 3.1A sequence{un}⊂Vis said to be an LP minimizing sequence for(P)if there exists 0<∈n→0 such that

Definition 3.2(P)is said to be LP well-posed if(P)has a unique solution and every LP minimizing sequence converges to a unique solution;(P)is said to be LP well-posed in the generalized sense if(P)has nonempty solution setV0and every LP minimizing sequence has a subsequence which converges to some point ofV0.

Proposition 3.1Letf(u)be defined by(8).Then we have the following statements:
(i)f(u)≥0,∀u∈K;
(ii)For anyu∈K,f(u)=0 if and only ifusolves HVI(A,f,j,K).
ProofIt is obvious that(i)holds.For(ii),we suppose thatu∈Kandf(u)=0,one has
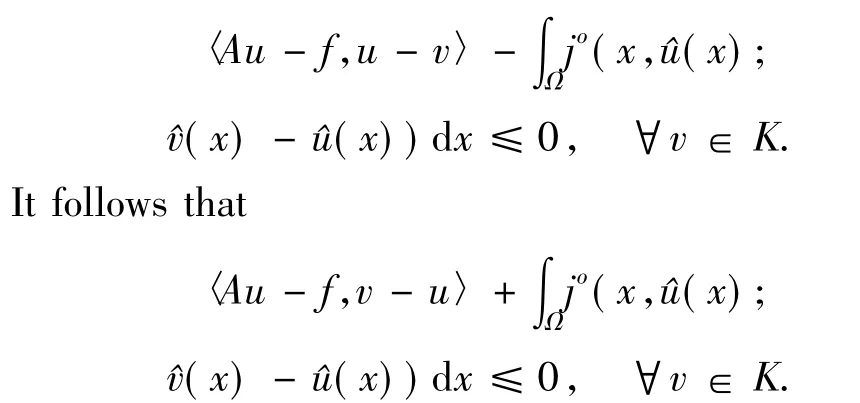
Conversely,ifusolves HVI(A,f,j,K),that isu∈Kand


A contradiction to(9).
Proposition 3.2LetA:V→V*be a continuous mapping.Thenf(u)defined by(8)is lower semicontinuous.
ProofFor anya∈R,and a sequence{un}⊂Vwithun→u* such that

Theorem 3.1HVI(A,f,j,K)is LP well-posed if and only if(P)is LP well-posed withf(u)defined by(8).
ProofBy Proposition 3.1,u'is a solution of HVI(A,f,j,K)if and only ifu'is an optimal solution of(P)withz=f(u')=0 andf(u)defined by(8).We first suppose that HVI(A,f,j,K)is LP wellposed.Let{un}be an LP minimizing sequence for(P),there exists 0 < ∈n→0 such that
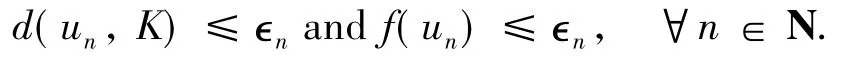
It follows fromd(un,K)≤∈nthatd(un,K)≤∈n< ∈n+,and there exists¯un∈Ksuch that,set¯un-un=wn,this implies thatun+wn∈Kwithwn→0.Sincef(un)≤∈n,one has

Then we have{un}is an LP approximating sequence for HVI(A,f,j,K),so we have(P)is LP well-posed withf(u)defined by(8).
Conversely,we suppose that(P)is LP wellposed withf(u)defined by(8).Let{un}be an LP approximating sequence for HVI(A,f,j,K),then there existswn∈Vwithwn→0 such thatun+wn∈K,and there exists 0 < ∈'n→0 such that

Set∈n=max{‖wn‖,∈'n},it follows thatd(un,K)≤∈nandf(un)≤∈nwith ∈n→0.Thus,{un}is an LP minimizing sequence for(P).This fact implies that HVI(A,f,j,K)is LP well-posed.
[1]Tykhonov A N.On the stability of the functional optimization problem[J].USSR J Comput Math Math Phys,1966,6:631-634.
[2]Zolezzi T.Extend well-posedness of optimization problems[J].J Optim Theory Appl,1996,91:257-266.
[3]Zolezzi T.Well-posedness criteria in optimization with application to the calculus of variations[J].Nonlinear Anal:TMA,1995,25:437-453.
[4]Zolezzi T.Well-posedness of optimal control problems[J].Control and Cybernetics,1994,23:289-301.
[5]Levitin E S,Polyak B T.Convergence of minimizing sequences in conditional extremum problem[J].Soveit Math Dokl,1996,7:764-767.
[6]Bednarczuk E M.Well-posedness of optimization problem[C]//Jahn J,Krabs W.Recent Advances and Historical Development of Vector Optimization Problems,Lecture Notes in Economics and Mathematical Systems.Berlin:Springer-Verlag,1987,294:51-61.
[7]Lucchetti R,Patrone F.A characterization of Tykhonov well-posedness for minimum problems with applications to variational inequalities[J].Numer Funct Anal Optim,1981,3(4):461-476.
[8]Hu R,Fang Y P.Levitin-Polyak well-posedness of variational inequalities[J].Nonlinear Anal:TMA,2010,72:373-381.
[9]Panagiotopoulos P D.Nonconvex energy functions,hemivariational inequalities and substationarity principles[J].Acta Mech,1983,42:160-183.
[10]Clarke F H.Optimization and Nonsmooth Analysis[M].Philadelphia:SIAM,1990.
[11]Motreanu D,Panagiotopoulos P D.Minimax Theorems and Qualitative Properties of the Solutions of Hemivariational Inequalities and Applications[M].Dordrecht:Kluwer Academic,1999.
[12]Naniewicz Z,Panagiotopoulos P D.Mathematical Theory of Hemivariational Inequalities and Applications[M].New York:Marcel Dekker,1995.
[13]Panagiotopoulos P D.Hemivariational Inequalities:Applications in Mechanics and Engineering[M].Berlin:Springer-Verlag,1993.
[14]Carl S,Le V K,Motreanu D.Evolutionary variational-hemivariational inequalities:existence and comparison results[J].J Math Anal Appl,2008,345:545-558.
[15]Goeleven D,Mentagui D.Well posed hemivariational inequalities[J].Numer Funct Anal Optim,1995,16:909-921.
[16]Liu Z H.Browder-Tikhonov regularization of non-coercive evolution hemivariational inequalities[J].Inverse Problems,2005,21:459-471.
[17]Xiao Y B,Huang N J.Browder-Tikhonov reguarization for a class of evolution second order hemivariational inequalities[J].J Global Optim,2009,45:371-388.
[18]Kuratowski K.Topology:1,2[M].New York:Academic Press,1968.

