基于组合时频分布的跳频信号分析

蔡卫菊，陈英芝

(长江大学 电子信息学院，湖北 荆州 434023)

基于组合时频分布的跳频信号分析

蔡卫菊，陈英芝

(长江大学 电子信息学院，湖北 荆州 434023)

针对常用的非线性时频分析方法不能较好地抑制交叉项干扰的问题,文中提出一种新的跳频信号时频分析方法。将组合时频分布TF方法用于跳频信号分析，提出了跳频信号持续时间、跳变时刻和跳频频率盲提取的改进算法，通过计算机仿真验证了该方法的有效性。

跳频信号；魏格纳分布；组合时频分析

跳频通信具有良好的抗干扰性、低截获概率及组网能力,采用跳频技术的各类收发信机在军事通信中得到了广泛的应用。传统的信号分析是建立在傅里叶变换的基础之上的，由于傅里叶分析使用的是一种全局的变换，无法表述信号的时频局域性质，而该性质恰恰是跳频信号这种非平稳信号最根本和最关键的性质。跳频信号属于非平稳信号，对其的盲检测和参数盲估计必须使用时频分析。常用的时频分析方法包括短时傅里叶变换(STFT)、魏格纳分布(WVD)、伪魏格纳分布(PWVD)与平滑伪魏格纳分布(SPWVD)等。但上述方法均存在缺点，无法满足跳频信号参数估计的实际应用要求[1]。

本文基于抑制WVD交叉项，将组合时频分布TF方法用于跳频信号分析，提出了跳频信号持续时间、跳变时刻和跳频频率盲提取的新算法，通过计算机仿真得到了更好的估值性能,验证了该方法的有效性。

1 时频分析

WVD时频分析是一种最基本的双线性时频分析，解析信号x(t)的自WVD定义为：

(1)

WVD在时频分布中具有理论上最高的时频分辨率，但是对于多分量信号或者单分量的非线性调频信号，WVD会产生交叉项干扰，在时频分布上会出现许多伪峰，影响了对信号的分析。因此，人们提出了加窗WVD，即伪WVD(PWVD)，PWVD定义为：

(2)

式中w(t)是一奇数长度的窗函数[2-3]。PWVD在时域加窗后，等效于频域作平滑滤波，在一定程度上抑制了频率方向上的交叉项干扰，但是信号在时域方向上的交叉项依然存在。因此，人们提出了平滑的PWVD，其本质是在PWVD基础上再做时域平滑滤波，从而进一步抑制干扰项。其表达式为：

(3)

式中：g(t)和w(t)是奇数长度的窗函数。SPWVD在时频域加窗平滑，大大消除了沿着频率轴、时间轴振荡的交叉项，但是降低了一定的聚焦性性能。本文在以上理论基础上提出了TF时频分析方法[4]。

谱图定义为短时傅里叶变换模的平方，其表达式为：

(4)

对谱图时频分布矩阵SPx(t,f)进行截断处理，得到SPx′(t,f)

(5)

式中：a为截断门限。门限不能固定，需随信号的强度而改变[5]。采取门限为时频矩阵的均值，设谱图离散化表示为SPx(n,k)，观测时段内时间采样点数为N，门限定义为：

(6)

将截断后的谱图时频矩阵与平滑伪WVD矩阵相乘(每行列的对应元素相乘)，得到组合时频分布TFx(t,f)，离散表达式为：

TFx=SPx′⊙SPWx=

(7)

其中，n=1,…,N；k=1,…,N；SPWx(n,k)为伪平滑WVD的离散化。

2 跳频信号

跳频信号是频率在一定范围内随时间伪随机跳变的一种信号形式，定义其简化模型为

(8)

式中：0≤t≤T，T为观测时间；

式中：Th为跳周期；T0为起跳时间；fk是跳变频率；N是跳变频率数；n(t)是附加噪声。

根据上述定义仿真产生一段跳频信号，包含 8个跳周期，1 024个采样数据，跳变频率分别为{15 25 30 20 35 40 10 25}MHz，采样率为65 MHz，跳周期为128个采样数据点，从0时刻开始起跳。其跳频图如图1所示，图中每一条线段代表跳频信号的一跳，称为一个hop。观测时间内有8个hop，记作hopk，k∈[1,8]。令Tk为第k个hop的时间中点，则跳频信号的每个hop实际上就是由以下三个参数唯一确定的时域不重叠的有限长的正弦函数：Tk为时域位置、fk为频域位置、Th为持续时间长度。只要估计这三个参数，就能根据相应的关系估计出跳频信号的跳周期、跳变时刻和跳频频率。

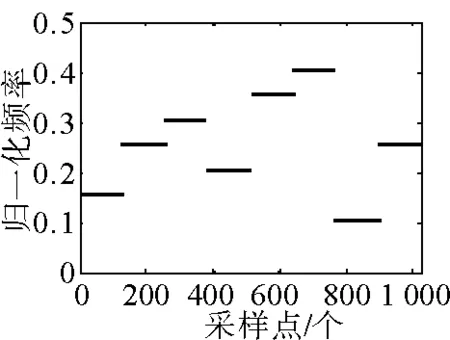
图1 跳频信号模型

由图2～图5分析可知，直接利用WVD变换对信号进行分析,存在交叉项干扰严重的问题；采用加窗的魏格纳-威尔变换法和平滑伪魏格纳-威尔变换法时,交叉项得到了明显的改善,但时频分辨率还不够理想；用本文所提的新方法对信号进行分析时，可以有效抑制交叉项,又能获得准确清晰的时频关系图[6]。

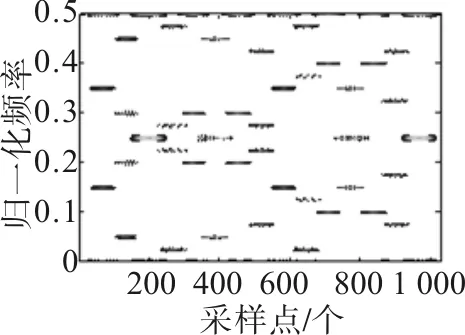
图2 信号WVD

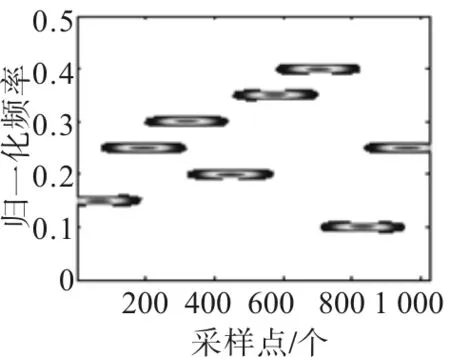
图3 信号PWVD

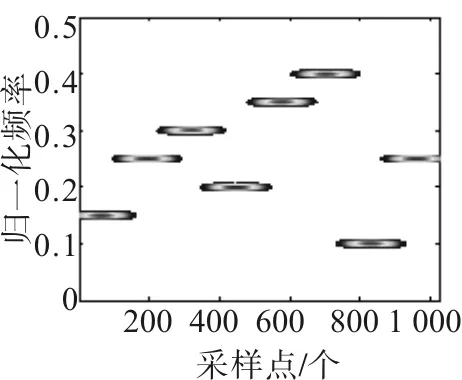
图4 信号SPWVD

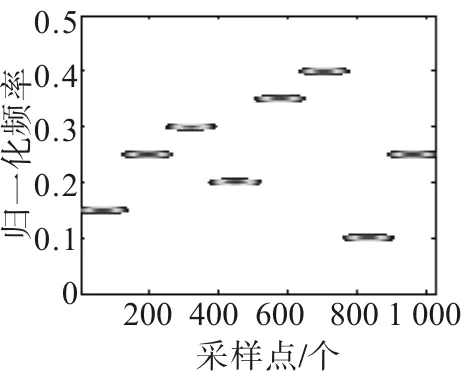
图5 信号TF

3 基于TF跳频信号跳周期估计算法

对观测信号采样后得到N长序列x(n),n=0,1,…,N-1,采样速率为fs,那么根据以上的思路利用TF来估计跳频信号跳周期的步骤如下[7]:

1)计算信号x(n)的解析形式z(n)；

2)计算z(n)的离散短时傅里叶变换模的平方SPz(n,k),对谱图时频分布矩阵SPz(n,k)进行截断处理;

3)计算z(n)的离散平滑伪WVDSPWz(n,k)；

4)将截断后的谱图时频矩阵SPz(n,k)与平滑伪WVD矩阵SPWz(n,k)相乘(每行列的对应元素相乘)，得到组合时频分布TFz(n,k)；

5)计算TFz(n,k)在每个时刻n的最大值,得到向量y(n);

6)用FFT估计y(n)的周期,得到离散跳周期的估计值Th。

4 实验分析

仿真结果表明,在信噪比大于-1 dB的条件下，用该算法来估计跳周期，受噪声的影响很小。表1给出的是不同信噪比条件下，周期的一次估计值，跳周期的实际值为1.96us。观测时间越长,参与运算的样本数目越多,则精度越高,估计值越精确,但要求计算时间也越长。

表1 不同信噪比条件下跳周期的估计(us)

5 结束语

本文利用TF良好的时频聚集性和抑制交叉项的能力,提出了一种基于TF的跳频信号跳周期估计算法。理论分析和仿真实验结果表明,该算法可以有效地估计出高速跳频信号的跳周期参数，提高了估计的准确性,降低了估计误差。

[1]张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社, 1998.

[2]Levent Aydin, Andreas Polydoros. Hop-timing estimation for FH signals using a coarsely channelized receiver [J]. IEEE Trans on Communications, 1996, 44(4): 516-526.

[3] Chung Char dir, Andreas Polydoros. Parameter estimation ofrandom FH signals using autocorrelation techniques[J]. IEEE Trans on Communications, 1995, 43(234): 1097-1106.

[4] Barbarossa S, Scaglione A. Parameter estimation of spreadspectrum frequency-hopping signals using time-frequency dis-tributions[C]// IEEE SPAWC, Apr.[s.l.]:IEEE Press，1997： 213-216.

[5] Monique P Fargues, Howard F Overdyk, Ralph Hippenstiel.Wavelet-based detection of frequency hopping signals [J].Thirty-First Asilomar Conference on Signals, Systems and Computers, 1997(1): 515-519.

[6] Zhu Wengui, Dai Xuchu, Xu Peixia. A design and realizationof the high-frequency reconnoitering system based on array sig-nal processing [J]. Journal of Chinese Computer Systems,2007,28(4):757-764.

[7]高宪军,陈超,张杰,等.抑制维格纳分布交叉干扰项的联合算法[J].吉林大学学报:信息科学版, 2009, 27(2): 127-132.

Analysis of Frequency Hopping Signal Based on Combined Time-frequency Distributions

CAI Weiju，CHEN Yingzhi

(College of Electronics and Information, Yangtze University, Jingzhou 434023, China)

A new method for time-frequency analysis of frequency hopping signal is presented, comparing to nonlinear time-frequency analysis of little suppression cross-term interference. The hop timing, hop duration and hop frequencies can be estimated without knowing any a priori knowledge based on TF method.Simulation results demonstrate it is effective and efficient.

frequency hopping signal; Wigner-ville distribution; time-frequency analysis

2013-09-18

蔡卫菊(1981-)，女，讲师，研究方向：信号处理。

TN911.7

A

10.3969/j.issn.1672-4550.2014.04.014