六边形孔蜂窝梁挠度的数值模拟与分析★

张春玉 沈 岩 陈 勇 孟祥民

(黑龙江科技大学，黑龙江 哈尔滨 150022)

·结构·抗震·

六边形孔蜂窝梁挠度的数值模拟与分析★

张春玉 沈 岩 陈 勇 孟祥民

(黑龙江科技大学，黑龙江 哈尔滨 150022)

利用有限元软件ANSYS，采用板壳单元和双线性随动模型，对六边形开孔的蜂窝梁在均布荷载作用下的挠度进行了数值模拟与分析，确定了影响其挠度的主要因素，并与实腹梁相对比，给出了适用于工程应用的挠度设计公式。

蜂窝梁，挠度计算，扩张比，修正系数

0 引言

六边形孔蜂窝梁是在实腹工字钢或热轧H型钢的腹板上按一定的折线进行切割、首尾错位组装、焊接而成的带有一系列孔洞空腹梁。蜂窝梁截面高度为原型实腹钢梁的1.3倍～1.6倍，因而较大地提高了钢梁的抗弯刚度和截面承载力，蜂窝梁腹板的孔洞既美观又便于安设管线。总体而言，蜂窝梁具有自重轻、抗弯刚度大、形式美观、经济等优点。因此，蜂窝梁在工程实际应用中具有良好的发展前景。国内外一些学者或基于费氏空腹桁架法[1]或采用有限单元法[2-4]或提出扩大系数法[5]推导出了蜂窝梁的挠度公式。美、英、日等国早已将蜂窝梁纳入设计规范，并给出了扩张比为1.5的各项参数，这极大地促进了蜂窝梁的工程应用。近些年，我国不少学者对蜂窝梁的研究虽取得了一些成果，但研究水平与发达国家尚有一定差距。为加快我国蜂窝梁设计理论的规范化，促进蜂窝梁在我国的工程应用，本文运用有限元软件ANSYS，分析了影响其挠度的主要因素，并给出了蜂窝梁挠度设计的实用公式。

1 有限元模拟与分析

本文工字钢选用Ⅰ36a，采用适于薄壁构件的壳单元Shell181单元[6]和经典的双线性随动强化模型[7]建立了有限元模型，利用有限元软件ANSYS对六边形开孔的蜂窝梁挠度的影响因素进行了分析，重点研究了扩张比及跨度与挠度的关系，并与等高同规格实腹梁(与蜂窝梁等高同规格)及原型实腹梁进行对比。

1.1 蜂窝梁的有限元模型

Shell181单元是具有强大的非线性功能、大变形及应力刚化功能的典型壳单元，用于蜂窝梁的模拟非常适合。本文所建的有限元模型忽略焊缝及残余应力的影响，考虑了几何非线性和材料的非线性。考虑几何非线性，可以准确分析材料的大变形；考虑材料的非线性，可以较详细地分析由轴力和剪力共同作用下构件抗弯能力的充分发展[8]。支座约束采用简支约束，通过对梁一端的下翼缘约束水平、竖向及侧向三个方向的位移、对另一端约束竖向位移和侧向位移加以实现。同时，为了防止构件在荷载作用下发生整体失稳，对蜂窝梁上翼缘施加侧向约束。为了防止蜂窝梁腹板在集中力作用下过早发生局部失稳，在支座处设置了支撑加劲肋。有限元模型如图1所示。

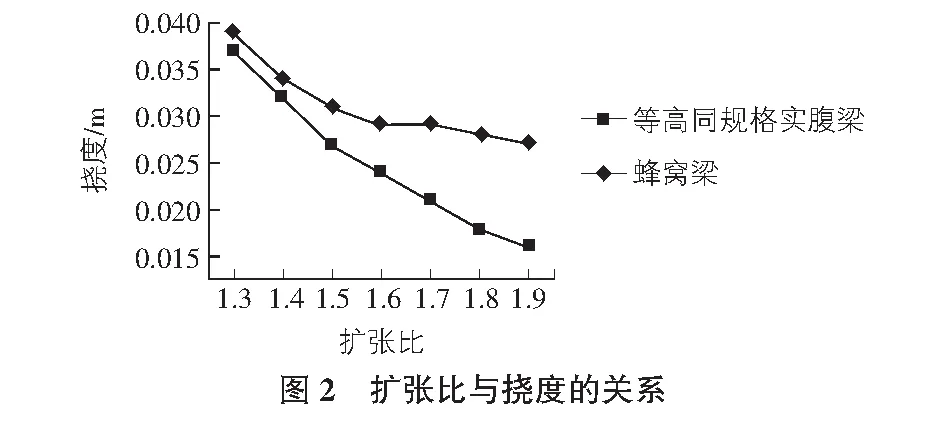
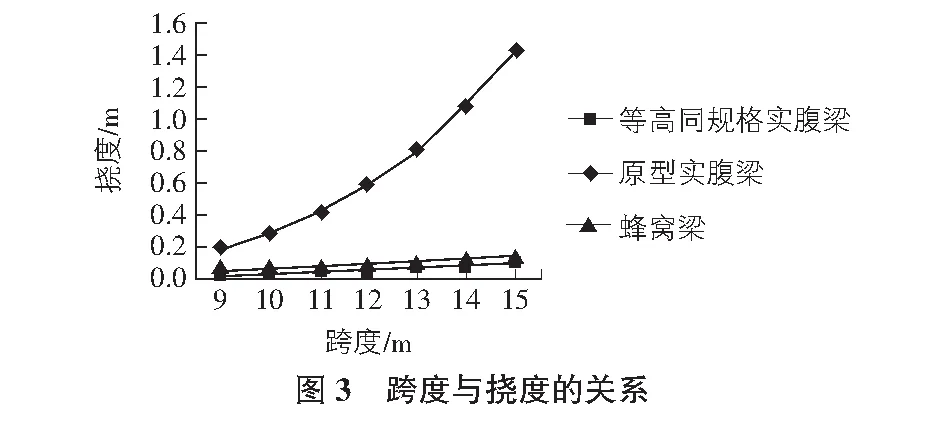
由欧美等国家的蜂窝梁设计规范可知，当蜂窝梁的跨度太小或扩张比K<1.3时，采用蜂窝梁并不能得到预期的效果。本文对跨度为9 m～15 m，扩张比K(蜂窝梁或等高同规格实腹梁的截面高度H与原型工字型钢的截面高度h之比)为1.3～1.9的蜂窝梁进行了模拟与分析。通过数值模拟可以发现，原型实腹梁的挠度远大于同跨度的蜂窝梁和等高同规格实腹梁。跨度为10 m蜂窝梁的扩张比—挠度曲线如图2所示。当梁跨度不变时，等高同规格实腹梁和蜂窝梁的挠度随扩张比的增加都减小，且实腹梁的挠度比等高同规格的蜂窝梁小，当扩张比K>1.5时蜂窝梁的挠度减小缓慢，这是由于随着扩张比的增加，梁高和抗弯刚度逐渐增加，同时孔洞对腹板的削弱作用越来越明显，剪力和截面次弯矩引起的挠度增加[9]。取蜂窝梁的扩张比K=1.5，跨度为9 m～15 m，通过数值模拟可得蜂窝梁跨度和挠度的关系曲线，如图3所示。由图3曲线的变化趋势可知，随着跨度的增加，蜂窝梁、等高同规格实腹梁及原型实腹梁的挠度都变大，但原型实腹梁挠度增长速率远大于蜂窝梁和等高同规格实腹梁；蜂窝梁和等高同规格实腹梁跨度与挠度关系近似一致。这是由于与原型实腹梁相比，蜂窝梁和等高同规格实腹梁抗弯刚度和截面承载力明显增大，而蜂窝梁由于腹板孔洞的削弱作用相对等高同规格实腹梁而言，抗弯曲变形的能力略有不足。

2 蜂窝梁的挠度计算公式推导

蜂窝梁弯曲变形过程与实腹梁相似，故本文只考虑弯矩产生的挠度，并在此基础上考虑由于孔洞对腹板削弱产生的挠度增大系数，定义蜂窝梁等效抗弯刚度EIm与等高同规格的实腹梁抗弯刚度EI的比值为修正系数β，即β=EIm/EI。

均布荷载作用下简支实腹梁挠度可由式(1)计算：

(1)

其中，v为实腹梁挠度；q为均布荷载；l为梁跨度；E为钢材弹性模量；I为实腹梁截面惯性矩。

均布荷载作用下简支蜂窝梁挠度可由式(2)计算：

(2)

其中，vm为蜂窝梁挠度；Im为蜂窝梁截面惯性矩；其他参数含义同式(1)。

由式(1)和式(2)得式(3)如下：

(3)

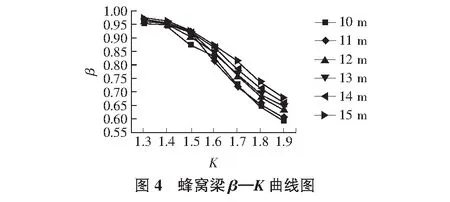
跨度l=10 m、不同扩张比的蜂窝梁与等高同规格实腹梁的数据对比如表1所示。通过数据分析可知，随着扩张比K的增加，β值大体上表现为快速减小趋势。不同跨度的β与K的关系曲线如图4所示。由图4可知，与扩张比K=1.3相比，当K=1.5时，β值的最大降幅接近9%；当K>1.5时，所有曲线均急剧下降，K=1.6与K=1.3时的β值相比，β值最大降幅就已接近17%。可见，扩张比过大的蜂窝梁已不适宜于用作承重结构。

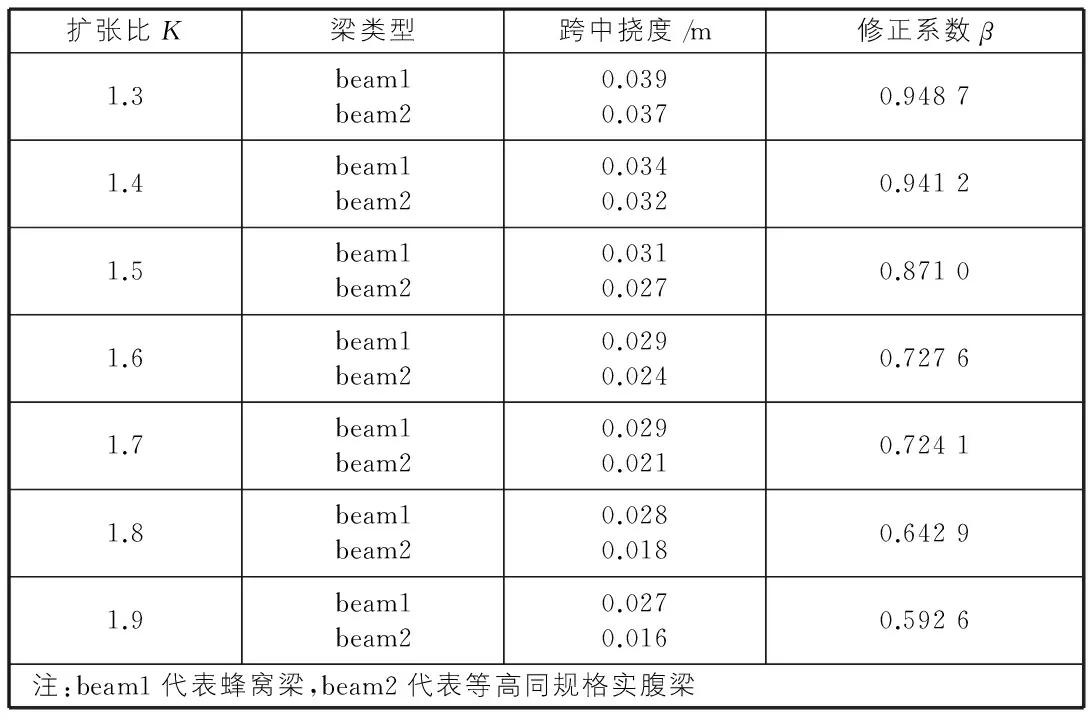
表1 跨度10 m蜂窝梁数据表

3 挠度公式拟合

由以上的分析可知，当扩张比1.3≤K≤1.5时，K为影响蜂窝梁挠度主要因素，当K>1.5时，孔洞对腹板截面的削弱作用明显，剪力和截面次弯矩产生的挠度过大，构件不适宜作为承重结构件。本文主要以K为设计参数，采用对数拟合的方法进行等效抗弯刚度修正系数β计算公式的拟合，形式如下：

首先确定二级潜水泵的选择原则，通常有恒压恒量供水、恒压变量供水、变压变量供水3种方式。为了管理方便，本工程采用恒压变量供水方式，即在供水压力一定的情况下保证用户的水量。泵池内安装4台200QGW360-40-75潜水泵及2台250QGW420-40-90潜水泵，根据供水压力和流量控制水泵运行。其安装方式均为自动耦合式装置，泵与耦合装置相连，耦合底座固定于泵坑底部，泵可在导轨（导杆）中上下移动，当泵放下时，耦合装置自动与耦合底座耦合，而提升时泵与耦合底座自动脱落。所有水泵附件全套安装完毕。

β=0.54+0.43(1+0.9×10-6×e8.3K)-1

(4)

其中，建议K值取1.3～1.5。在GB 50017-2012钢结构设计规范征求意见稿中，给出了蜂窝梁挠度计算公式如式(5)：

(5)

其中，Mkmax为梁跨中最大弯矩标准值；I0为当量实腹梁的截面惯性矩；η为考虑空腹截面影响的增大系数；[v]为受弯构件的挠度允许值。

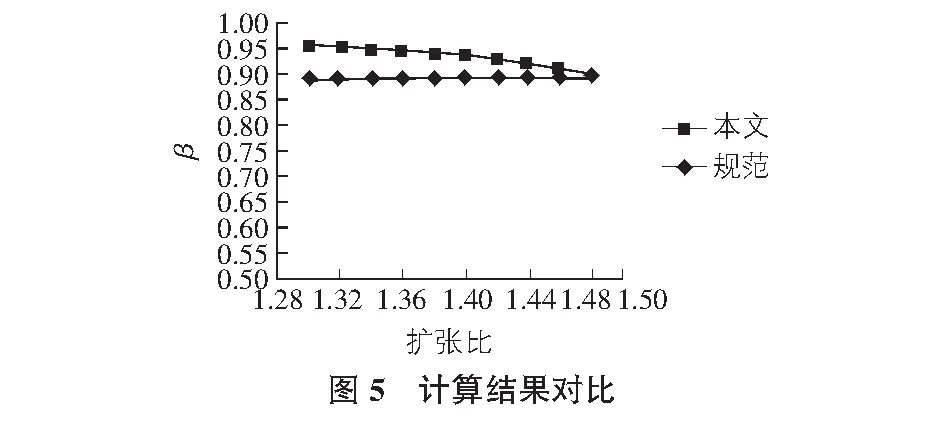
为验证拟合公式的准确性，现将以上两式的计算结果进行对比，例如，取K=1.4，跨度为15 m，均布荷载为5 kN/m，β=0.931，规范公式算得蜂窝梁在此均布荷载下挠度为0.052 m，等高同规格实腹梁挠度为0.046 m，则由规范公式可得到β=0.885，以此类推，两式结果对比如图5所示。可见，本文公式计算结果β大于规范公式，则本文公式计算的挠度小于规范结果，即若采用式(4)进行蜂窝梁设计偏于经济，采用式(5)则会偏于安全。

4 结语

本文利用有限元软件ANSYS分析了蜂窝梁弯曲变形的全过程，找出了影响挠度的主要因素，并给出了实用的挠度计算公式，对该新型构件的推广和应用具有积极意义。经过数值分析，本文得出了如下结论：

1)由于孔洞对蜂窝梁腹板截面的削弱作用，扩张比K>1.5时，剪切变形产生的挠度不可忽略。

2)与同跨度原型实腹梁相比，蜂窝梁的抗弯刚度和截面承载力大幅度提高。

3)其他因素相同的情况下，蜂窝梁的挠度随着扩张比K的增大而减小，当K>1.5时，增加扩张比对构件挠度的贡献作用并不明显。这是由于孔洞对腹板截面削弱过大，因此除特殊要求外，不建议在工程上使用。

4)修正系数β随扩张比K的增大而减小，且减小作用显著。扩张比K=1.3的蜂窝梁的β值与K=1.9的蜂窝梁挠度相比，减小了31%左右，尤其当K>1.5时，蜂窝梁的抗弯刚度明显小于等高同规格实腹梁，故扩张比K取1.3～1.5为宜。

5)当扩张比1.3≤K≤1.5时，可用式(1)指导设计规范进行简化计算及辅助设计，可取得较好经济效果。

[1] 李鹏飞，王新敏，袁 泉，等.基于等效面积法的蜂窝梁挠度计算方法研究[J].石家庄铁道大学学报(自然科学版),2011，3(24):8-11.

[2] 杨永华，陈以一.连续开孔梁的抗弯刚度和挠度的等效计算[J].结构工程师,2006,22(3):33-35.

[3] 李鹏飞，姚谦峰.蜂窝梁应力和挠度计算方法[J].建筑结构,2011,42(2):52-55.

[4] 冯春燕，于大永.蜂窝梁挠度计算方法研究[J].四川建筑科学研究,2012,38(1):65-69.

[5] 何一民，李 鹏，鸿于力.蜂窝梁挠度的实用计算方法[J].工业建筑,1994(3):9-15.

[6] 王新敏.ANSYS结构分析单元与应用[M].北京：人民交通出版社，2011:274-276.

[7] 杨 坛.基于ANSYS的圆孔蜂窝梁承载力研究[D].南宁：广西大学，2007:15-17.

[8] 张春玉，朱柏杰，乔 牧，等.六边形孔蜂窝梁抗弯承载力的数值模拟与分析[J].黑龙江科技学院学报,2013,23(6):577-580.

[9] 郑 懿，杨俊杰，王森军，等.蜂窝梁的挠度影响因素分析[J].浙江工业大学学报，2007,35(6)：695-698.

The numerical simulation and the analysis method for the deflection of hexagon-hole castellated beams★

ZHANG Chun-yu SHEN Yan CHEN Yong MENG Xiang-min

(HeilongjiangUniversityofScienceandTechnology,Harbin150022,China)

Using finite element program ANSYS, with shell element and bilinear kinematic model, the hexagonal hole deflection of castellated beams under the action of load are analyzed by numerical simulation. According to the uniform load, lateral displacement by castellated beam constraint, determine the main factors which influence the deflection of the beam, and with the comparison, design formulas are given for engineering application.

castellated beams, deflection, dilatation ratio, modified coefficient

1009-6825(2014)15-0024-03

2014-03-16★：黑龙江省科学技术研究项目(项目编号：12521476)

张春玉(1971- )，男，博士，教授； 沈 岩(1988- )，男，在读硕士； 陈 勇(1977- )，男，讲师； 孟祥民(1967- )，男，工程师

TU311.4

A