BRT停靠时间的统计估算研究
侯 文 宇
(大连市公安局交警支队科技处,辽宁 大连 116011)
BRT停靠时间的统计估算研究
侯 文 宇
(大连市公安局交警支队科技处,辽宁 大连 116011)
分别对估计停靠时间的计算方法和停靠时间总体分布规律进行了研究,在估计停靠时间方法中,提出了最繁忙车门的服务人数和上下车总人数的比例有其规律性的观点,在总体分布规律的方法中,验证了其服从威布尔分布的事实。
停靠时间,车门选择,威布尔分布,BRT,公交站点
0 引言
作为一种高效的公共交通工具,BRT被越来越多的城市所使用,针对BRT的有关研究也多了起来。有关BRT的调度、BRT公交优先信号控制等问题的研究[1,2]能更加有效的运营BRT,提高其工作效率。BRT停靠时间的研究就是其中一个重要的组成成分。
公交停靠时间是指公交车在站点处停靠所耗费的时间,是整个公交运行中重要的部分。甚至有研究提到在美国,公交车的停靠时间能占据总运行时间的26%[3]。对常规公交车的停靠时间问题,已经有一定的研究成果:Adamski提出因乘客惯性行为和老年人以及携带行李的出行人而造成的服务延迟情况[4];Guenthner和Hamat分析了收费系统对停靠时间的影响程度[5];彭庆艳,杨东援在构建基本模型的基础上,针对时段、地段等不同因素,用系数对基本模型进行修正,给出了修正系数的求值方法以及推荐取值范围,并针对公共汽车等待、数次停站等情况给出了模型的变化形式[6];吴洋,罗霞针对乘客的行为,对公交车的停靠时间进行了分析[7];Kraft和Bergen还通过回归模型分析出高峰期和非高峰期,前后门对停靠时间产生的不同影响[8];Lin和Wilson采用线性回归模型和非线性回归模型两种方法对停靠时间进行了研究[9]。在此基础上,本文结合大连BRT的实际调研数据,对BRT的停靠时间进行了具体分析。
1 问题描述
公交车的停站主要分为五个阶段:停站车站阶段、开门阶段、上下客阶段、关门阶段以及驶离车站阶段[10](见图1)。在特殊情况下,还会因为有串车出现,导致等待停车进站以及由于前车乘客多而阻挡离开的等待离开阶段,还有可能出现额外乘客出现导致的二次停车阶段(图1中Extra1和Extra2)。本文主要探讨基本阶段。
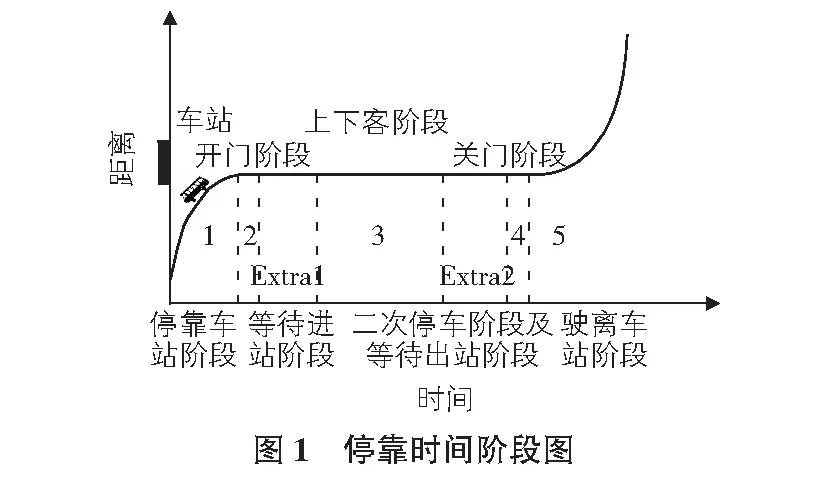
大连BRT于2008年1月15日正式开通投入运营,采取站外售票,各车门不限上下车的方式,并拥有4个车门的大车以及3个车门的小车间隔运营,有很鲜明的特点。全程共13个站点,在研究过程中,选取了车家村站、春柳站以及周水子前三站进行调查分析。
2 停靠时间的预测方法
2.1 分解分析
通过公交车停靠时间的五个阶段的划分可以看出,停站车站以及驶离车站的两个阶段,主要与公交车的性能、司机的开车习惯等有关,相应到具体BRT而言,固定的车型、司机经验也比较丰富,在调查过程中发现,极少有司机会很早进入空挡滑行至站台,大多是在一段距离内刹车,所以这两方面变化很小,可以近似视为固定值。而对于开关门两个阶段而言,因为车型相对较新,开关门的时间和速度都比较稳定,在1.5 s左右。所以可以看出,停靠时间的主要影响因素,实际上是在上下客阶段。
2.2 上下客阶段分析
上下客的阶段,主要是在开门后乘客下车以及乘客上车的这段时间,主要影响这段时间长短的有两个方面:上下车乘客的人数以及乘客上下车的速度。这段时间的计算可以用式(1)表示:
T=max{Tb×Nb+T1×N1}+c
(1)
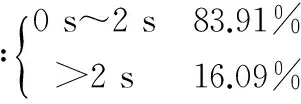
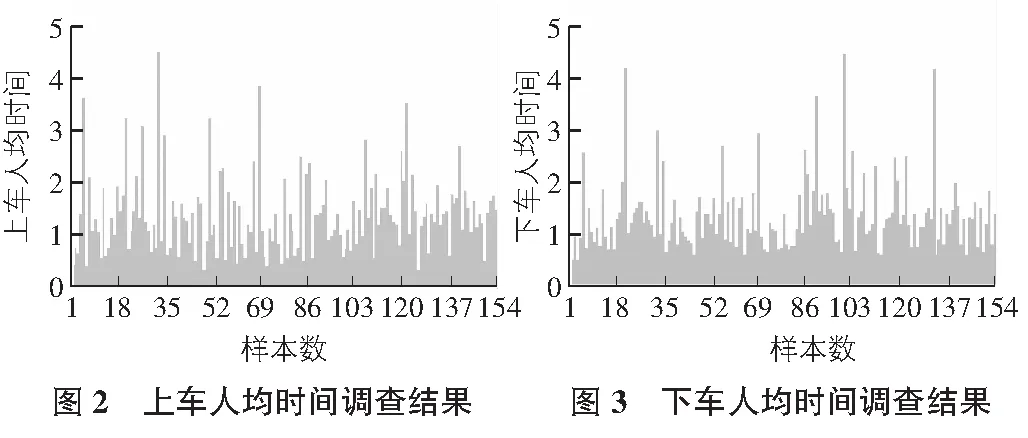
乘客上车人均时间调查结果见图2。
乘客下车人均时间调查结果见图3。
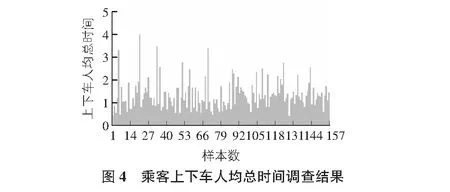
乘客上下车人均总时间调查结果见图4。
可见,大连BRT因其低地板、站外售票等因素,使得上下车所需要的时间接近,上文的数据已经说明这一问题,又因上下车乘客对车门的选择互相影响,所以在最忙车门人数的预测时,用上下车总乘客数估计,故而可以将停靠时间与总人数的关系,表示为分别与上、下车的总数的关系,式(1)记作:
T=max{T′×Ni}+c
(2)
其中,T′为上下车乘客平均花费的时间;Ni为第i个车门上下车人数和;c为回归系数。
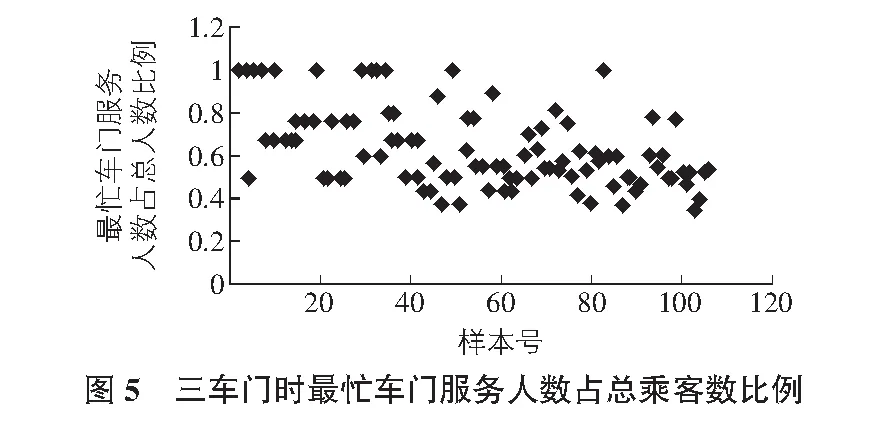
式中的max{}表示最忙碌的那一个车门,在调研的过程中发现,虽然有3个或4个车门,但乘客们选择有其偏好,导致了车门的服务率是不同的,往往集中于某一两个车门,所以这里的max{}并非总人数/车门数那么简单。较容易得到的数据是上下车总人数,所以服务量最大的车门的上下车人数占总人数的比例是计算的关键。理论上3车门的车比例为[1/3,1],4车门的车比例为[1/4,1]。
图5,图6中的样本按总人数由少到多排号,如出现乘客数为1的有3个,即样本号1~3为乘客数1的时候,乘客数为2的有4个,即样本号为4~7为乘客数2的时候。由图5可见3车门的车总乘客数N的范围为:
1时,样本号为1~3,显然是只有一个门上下车人数为1;
2时,样本号为4~7,比例为1的概率比0.5的概率大,即两个人在同一个车门上下车的可能性比分别使用两个不同车门概率大;
[3,6]时,样本号为8~42,最繁忙的车门的服务人数占总人数的比例最大的是[0.6,0.8],还有部分出现1,也就是所有人集中在一个门上车。因为这个范围内,乘客较少,多集中上下车;
[7,+∞]时,样本号在43之后的,这一比例多集中于[0.4,0.6],尤其是50%这个比例出现的次数非常高。
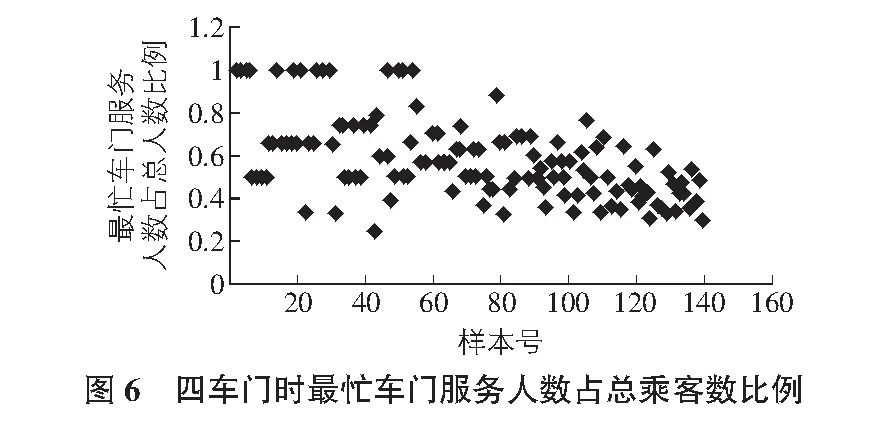
同样找出一定规律,4车门乘客数N的范围为:
1时,即样本号1~3,这个比例同样显然也是1;
[2,5]时,样本号为4~46,最繁忙的车门的服务人数占总人数的比例最大的是[0.5,0.8],此时最繁忙的人数大多为2人~3人,值得一提的是,2人时,0.5的概率比1大,和3车门时不太一样;
[6,12]时,样本号为47~102,这个比例在[0.5,0.7]之间比例较大,人们更多集中于第二或第三个车门上下车;
[13,+∞)时,样本号为103之后的,这个比例又有所下降,[0.3,0.6]之间较多,可见大车在人多时才会有很多人愿意选择较远的门。
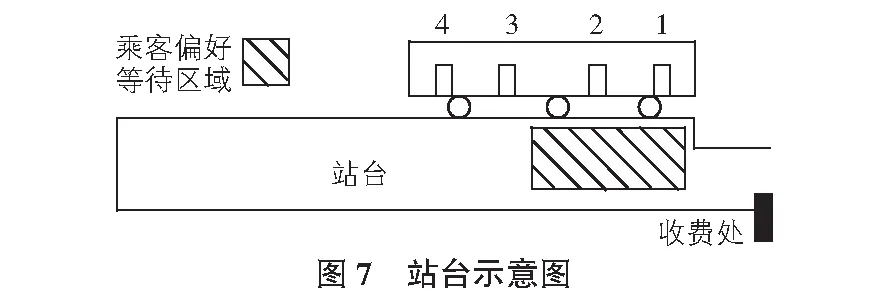
可以看出,人们对车门的选择分布并不均匀,虽然有多个门,但多数情况下有近一半的人会集中选择其中一个。观察发现,两种车型(尤其大车)的最后一个车门的服务频次远远小于前面的车门,小车的第二个车门和大车的前两个车门,经常成为最繁忙的车门。分析其原因,我们发现人们在进入站台后,大多选择停车时前面的车门所在的站台位置(如图7所示)。车到达站点后,乘客对车门的选择主要因素有:离车门的距离、车门下车人数、上车排队长度、车内拥挤程度等。往往都选择就近上车,即使某个车门已经空闲,但也不一定有太多人愿意移动到较远的车门,而更愿意等待并不长的时间去上前面的门。只有在排队长度十分明显的情况下,才有人去选择离自己较远但空闲的车门。
根据上述规律,式(2)中的人数可以通过总人数的检测来估计。接下来是对时间的估计。
2.3 停靠时间的估计
上下车纯服务时间与最忙车门服务人数之间的关系,采用线性回归方式(见图8)。
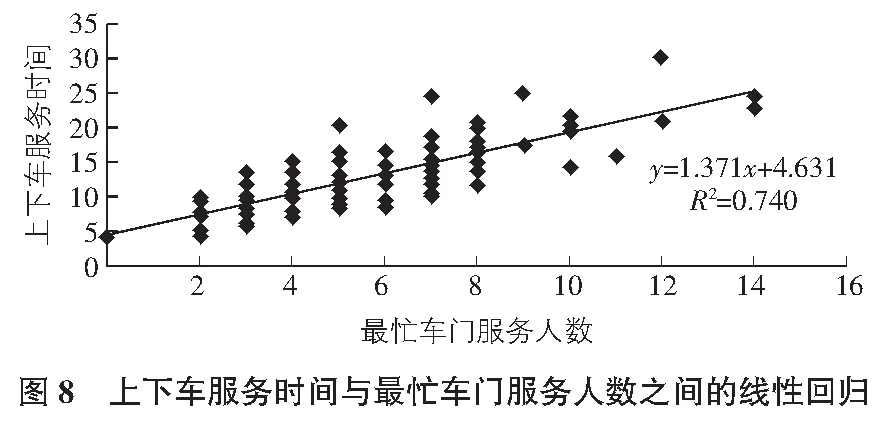
式(2)的回归结果为y=1.371x+4.631(y代表时间,x代表最繁忙车门上下车人数),回归方程的正相关系数R2=0.74,回归F统计值为164.096,可以通过显著水平为0.05的检验。这里的系数1.371,与上面统计的乘客平均所需时间的数据1.374 067相差在合理范围内,所以说明该回归方程有一定合理性,可以接受。
R2=0.74的结果并非完美,从散点图中也可以看出,回归到一条直线并不能完全准确的计算出停靠时间与最繁忙车门的上下客人数,更像是两条线划定的范围内。从边缘取点并进行线性回归计算,可知能包含在y=1.37x+8.311以及y=1.281x+2.158之间,上述两条边界方程的正相关系数R2=0.918,回归F的统计值=67.306和R2=0.952,F=217.965。相比单一直线的回归要准确的多,其系数也更贴近调查的乘客上下车平均耗时。所以我们可以认为,停靠时间与最忙车门的上下车人数的关系,是介于y=1.37x+8.311以及y=1.281x+2.158的。
综上就可以先从上下车总人数知道最忙车门的上下车人数和,再通过式(2)的回归结果,就估算出BRT的停靠时间。
3 结语
本文对大连BRT停靠时间的估计方法进行了研究,了解了停靠时间的过程和其中的规律。揭示了在多门可以同时上下客的情况下从乘客选择车门的规律上,发现了总服务人数与最繁忙车门服务人数之间的联系,并由此通过总人数可以估算出停靠时间的长短。
[1] 徐洪峰,王殿海.BRT优先控制交叉口的机动车相位固定最小绿灯时间计算方法[J].吉林大学学报(工学版),2009,39(1):92-97.
[2] Werner J.Houston Metro Plans to Deploy a More Intelligent Transit Priority Scheme.Newsletter of the ITS Cooperative Deployment Network,National Associations Working Group for ITS,December 2002.Available:www.nawgits.com/icdn/ivoms_tp.html.
[3] Levinson H.S.Analyzing Transit Travel Time Performance.In Transportation Research Record 915,TRB,National Research Council,Washington,D.C.,1983:1-6.
[4] Adamski A.Probabilistic Model of Passenger Service Processes at Bus Stops[J].Transportation Research,1992,26(4):253-259.
[5] Guenthner R.P.,K.Hamat.1988.Transit dwell time under complex fare structure[J].Transportation Engineering Journal of ASCE,2010,114(3):367-379.
[6] 彭庆艳,杨东媛.公共汽车中途站停靠时间模型[J].长安大学学报(自然科学版),2002,22(1):60-62.
[7] 吴 洋,罗 霞.公交车辆停靠时间与乘客行为的关系[J].西南交通大学学报,2007,42(2):243-248.
[8] Kraft W.,T.Bergen.Evaluation of Passenger Service Times for Street Transit Systems.In Transportation Research Board 505,TRB,National Research Council,Washington,D.C.,1974:13-20.
[9] Lin T.M.,N.H.M.Wilson.Dwell Time Relationships for Light Rail Systems.In Transportation Research Record 1361,TRB,National Research Council,Washington,D.C.,1992:287-295.
[10] Transportation Research Board,Highway Capacity Manual,National Research Council,Washington D.C.,2000.
The research of statistical estimation and distribution about BRT dwell time
HOU Wen-yu
(TechnicalDivisionofTrafficPoliceBrigadeofDalianPublicSecurityBureau,Dalian116011,China)
Analyzed the calculation method in estimating about the dwell time, the other is the distribution of it. About the method, the relationship of the number of the passengers passing the busiest door and the whole boarding and lighting passengers have its rule. About the distribution, it is proved that it comply with the law of Weibull distribution.
dwell time, door selection, Weibull distribution, BRT, bus station
1009-6825(2014)15-0002-03
2014-03-18
侯文宇(1971- ),男,高级工程师
TU984.191
A

