全厂断电引发的严重事故下蒸汽发生器传热管蠕变失效风险研究

陈宝文，毛 欢，孔翔程，陈 彬

(1.中国核动力研究设计院，四川 成都 610041；

2.环境保护部 核与辐射安全中心，北京 100082)

作为响应1985年美国NRC严重事故政策申明的重要举措，美国核工业界发布了严重事故关闭导则，多个国家的核电厂在此导则基础上，吸收严重事故的研究成果，发布了针对自己电厂特点的严重事故管理导则(SAMG)。

与通常核电厂所采用的事件导向规程所不同的是，由于严重事故管理要求在有限的时间、资源、信息等条件下，克服恶劣环境和复杂事故现象的影响，进行正确的决策以控制严重事故的发展并缓解其事故后果。在SAMG的操作中需明确列出执行操作后可能带来的各种负面影响，并提示技术支持中心在执行相应操作时必须详细评价其潜在后果。导则“向蒸汽发生器中注水(SAG-1)”中，特别强调了在严重事故下通过自然循环冷却堆芯时，蒸汽发生器(SG)传热管在高温和一、二次侧高压差的作用下可能出现蠕变失效。

由于SG传热管破裂(SGTR)的后果是安全壳被旁通，堆芯中裂变产物将直接释放到环境中。所以国际上从1998年起，NRC就在报告NUREG-1570中，基于美国西屋公司设计的三环路Surry电厂对严重事故[1]导致的SGTR进行了初步研究，结果表明通过改进电厂设计能降低SGTR的风险；Majumdar[2]从结构力学的角度对严重事故条件下SG传热管的完整性进行了研究，但未考虑系统间的相互影响和不同严重事故序列的特点；Liao等[3]着重研究了异物等导致SG传热管缺陷，对严重事故条件下发生SGTR可能性的影响，并利用蒙特卡罗方法研究了稳压器波动管失效前出现SGTR的概率；Bang等[4]利用MELCOR程序研究了韩国OPR1000电厂在SBO引发的严重事故下的SGTR风险；Peng等[5]则主要从降低大量放射性释放频率的角度，探讨应如何采取恰当措施降低发生SGTR的可能性；Bansah等[6]则通过Steam Generator Mitigation Program程序分析SG内的回流率和交混份额，探讨了严重事故下热管段自然循环与SG传热管蠕变失效之间的关系。国内对作为设计基准事故下的SGTR探讨较多，多家研究机构从破口面积、操纵员干预时间窗口、直流蒸汽发生器SGTR破口特性、传热管材料腐蚀机理、传热管运行老化以及AP1000核电厂事故瞬态特性的不同角度对SGTR事故开展了研究；此外，SGTR严重事故后果、高压熔堆严重事故序列、AP1000的SGTR严重事故裂变产物行为，以及传热管管壁减薄后对SGTR可能性的影响在国内也得到了初步研究。

本文采用严重事故系统分析程序，针对秦山二期核电厂两回路设计特点研究SBO引发的严重事故进程中SG传热管、稳压器波动管及热管段出现蠕变失效的可能性。进而探讨秦山二期核电厂全厂断电引发的严重事故下因SG传热管蠕变失效而导致安全壳旁通的风险。

1 SG传热管蠕变失效模型

在持续载荷作用下，材料随时间的推移出现塑性变形。此时材料所承受的应力并未达到屈服的极限应力，其温度也并未达到熔点，该现象称为蠕变失效，而影响它的主要因素除材料本身的特性外，还与材料所处的外界环境，特别是材料所承受的压力和温度有关。对同一结构而言，其应力越大，温度越高，达到蠕变失效的时间也就越短。

蠕变失效机理图(图1)是描述特定材料的蠕变失效与应力和温度之间关系的一种方法。图中的横坐标为归一化温度，即材料温度T与材料熔点Tm之比，纵坐标为材料的切应力σ与剪切模量G之比。

Larson等[7]对316型不锈钢不同温度下的蠕变失效过程进行了实验研究，并提出蠕变率r可用Arrhenius关系式来描述，即：

r=Ae-ΔH/RT

(1)

式中：A为常数；R为普适气体常数；T为绝对温度；ΔH为蠕变失效过程的活化能。

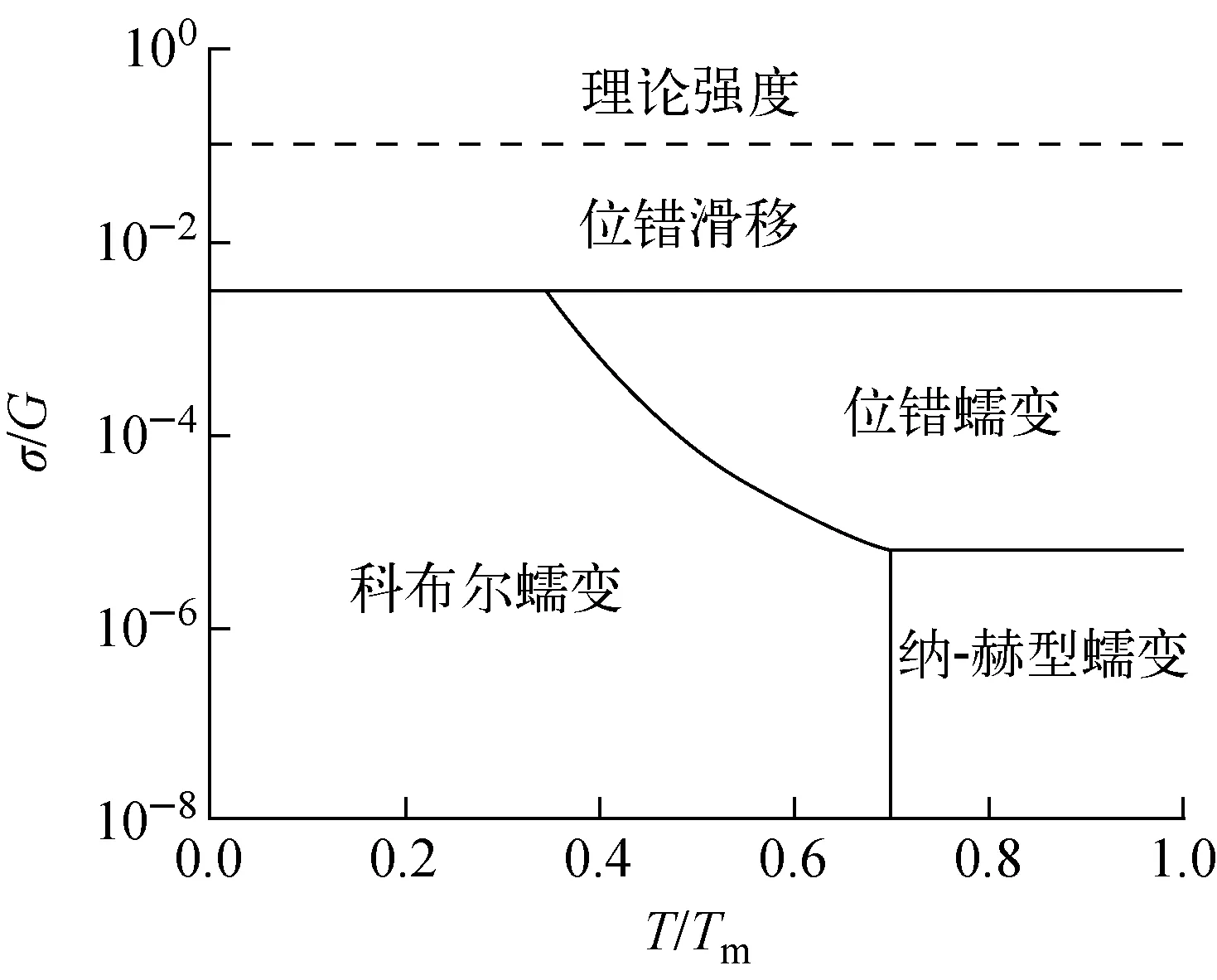
图1 蠕变失效机理图

假设蠕变率与时间Δt呈反比，即r=Δl/Δt，则用下式描述活化能与蠕变失效时间的关系：

ΔH/R=T(B+ln Δt)

(2)

其中，B=ln(A/Δl),Δl为蠕变量。

假设蠕变失效的活化能与材料所承受的应力无关，即能通过实验得到不同材料在不同温度下蠕变失效应力与时间的关系，从而确定式中相关参数。Larson与Miller实验确定的关系如图2所示，而这一实验关系式也进一步被NRC的ASME材料蠕变行为研究证明是保守的。

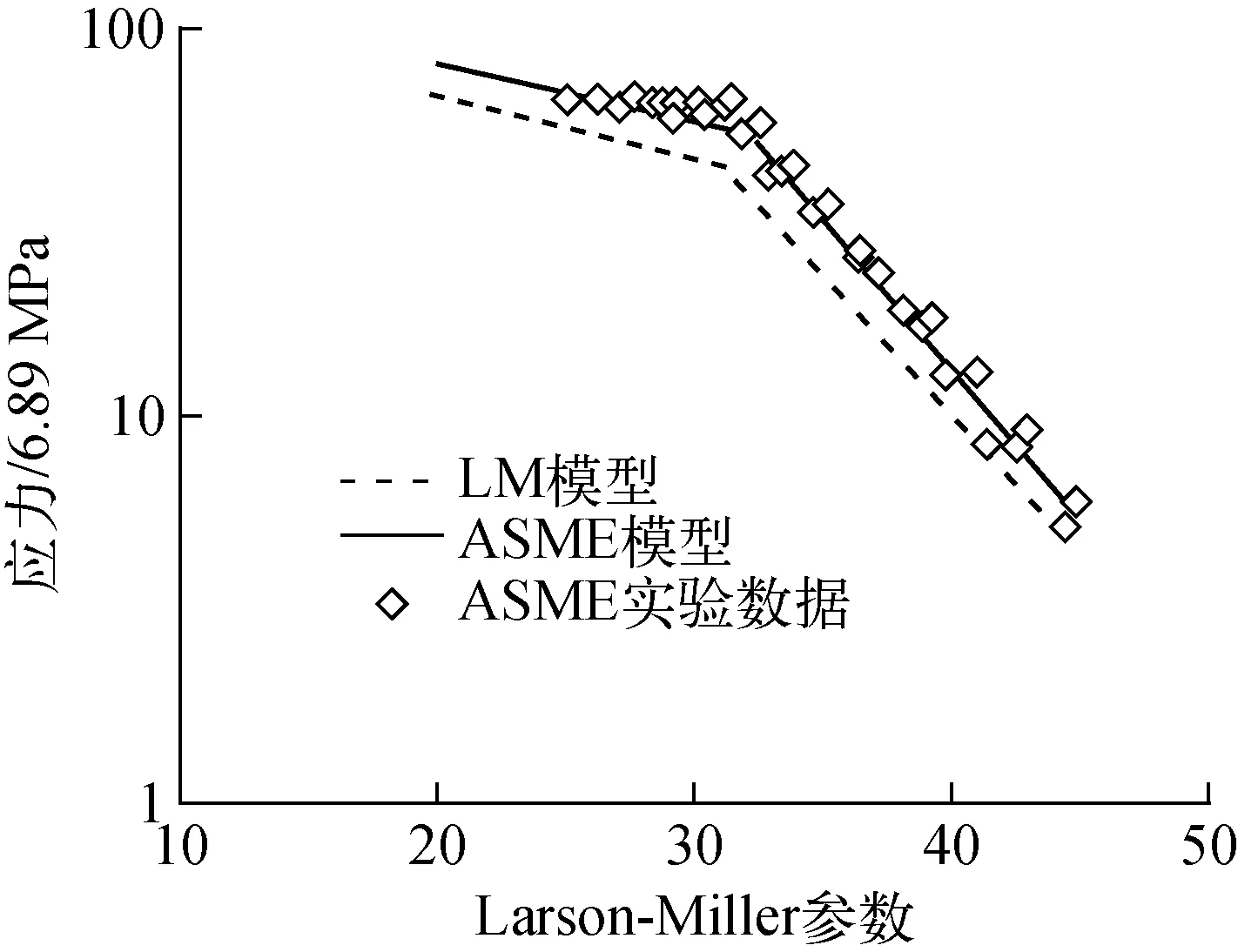
图2 Larson-Miller蠕变失效模型

以上Larson-Miller参数被广泛用于MELCOR、MAAP、SCDAP等严重事故分析程序中，描述钢结构材料的高压高温蠕变失效过程。

秦山二期核电厂蒸汽发生器传热管采用了不同于不锈钢的Inconel 690合金，在本研究中针对该材料特点采用如下模型描述Inconel 690蒸汽发生器传热管的蠕变失效：

(3)

p=-11 333lgσ+43 333

(4)

(5)

式中：p为传热管内的压力，kPa；T为传热管管壁的温度，K；σ为传热管结构承受的机械应力，kPa；R为蠕变失效参数，当R积分值为1时，结构出现蠕变失效，而该时刻tf即为蠕变失效时间；mp为局部裂纹应力修正因子。在本研究中还进一步考虑了传热管可能存在的周向及轴向缺陷的影响，认为轴向裂纹对失效压力的影响可用下式表示：

(6)

其中，

(7)

(8)

式中：Rm为平均半径；h为传热管壁厚；a为裂纹深度；α为修正函数；m为贯穿裂纹应力修正因子。

所以由裂纹深度的测量误差可能引起的预测失效压力误差为：

(9)

现阶段缺少电厂特定运行数据，本文根据PNNL(Pacific North National Laboratory)、INEL(Idaho National Engineering Laboratory)及EPRI(Electric Power Research Institute)严重事故条件下SGTR的相关实验，描述mp的标准偏差为：

(10)

即在利用式(5)预测蠕变失效时，蠕变失效参数服从均值μ=1、标准偏差为0.4的正态分布。

2 蠕变失效风险评价

本文以严重事故系统分析程序的秦山二期核电厂模型[8]为基础，研究秦山二期核电厂SBO引发的严重事故事件序列。发生SBO的时间为事故序列的起始点，控制棒因断电自动下落，反应堆安全停堆。由于丧失全部交流电源，应急柴油机也无法启动，操纵员通过二次侧汽动泵向SG内注水以带走堆芯余热。严重事故序列假设SBO后辅助给水系统不可用，在无给水补充的情况下操纵员开启大气释放阀排出热量的同时，使得SG内水装量不断减少。虽然反应堆冷却剂系统内从堆芯、热管段至SG处建立的自然循环在一段时间内能带走堆芯的部分热量，但随着SG水位不断下降，其传热能力不断恶化，热管段和SG传热管内的温度将持续升高。随温度的升高，水体积的膨胀和热量的增加均会导致压力的不断上升；到达稳压器释放阀开启整定值后，冷却剂通过释放阀排放的同时，也促使高温、高压的冷却剂从热管段通过稳压器波动管向稳压器流动。随着温度、压力在SG传热管、稳压器波动管和热管段的累积作用，这3处均可能出现蠕变失效。

为使该程序的秦山二期核电厂模型能更好地模拟自然循环对热管段、稳压器波动管及SG传热管的影响，在过去模型的基础上对反应堆冷却剂系统的热管段和SG传热管部分的控制体进行了进一步细化(图3)。

图3 严重事故自然循环的程序建模

由于蠕变失效是一高压、高温的累积作用，反应堆冷却剂主泵轴封出现破口后会使反应堆冷却剂系统的压力下降，进而降低出现蠕变失效的概率。所以在分析时假设整个SBO引发的严重事故进程中反应堆冷却剂主泵不会出现轴封泄漏。程序计算得到的事故序列列于表1。

表1 SBO事故事件序列

本文研究SBO引发的典型高压熔堆严重事故序列，反应堆冷却剂系统压力维持在稳压器释放阀开启压力整定值。不同热构件温度随时间的变化示于图4。

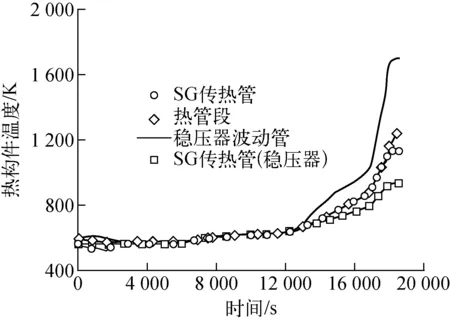
图4 不同热构件温度随时间的变化

将图4中温度随时间的变化函数代入式(5)并随时间积分，可得到蠕变失效参数的概率密度分布函数。该函数再经时间的重积分，得到秦山二期核电厂SBO引发的典型高压熔堆严重事故序列中SG传热管、热管段及稳压器波动管出现蠕变失效的累积概率(图5)。该累积概率表征了SG传热管、热管段及稳压器波动管的蠕变失效风险：只有相当短的时间内(15 920～16 400 s)存在SG传热管蠕变失效的可能。SBO事故发生后约16 250 s时，稳压器波动管出现蠕变失效的概率开始超过SG传热管，当事故进行至16 600 s时，稳压器波动管及热管段发生蠕变失效的概率趋近于1，而此时SG传热管蠕变失效概率仅为0.6。无论是稳压器波动管还是热管段的蠕变失效均会导致反应堆冷却剂系统的被动卸压，进而避免SG传热管的蠕变失效。

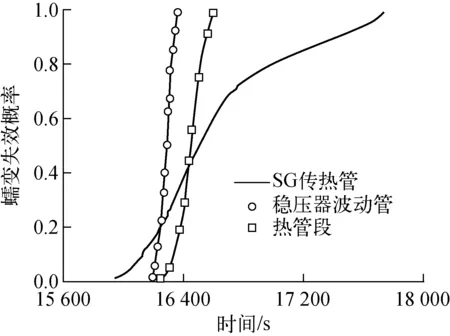
图5 不同热构件蠕变失效概率

3 结论

本文结合秦山二期核电厂SG的设计特点，利用严重事故系统分析程序，基于SG传热管蠕变失效概率模型对SBO引发的典型高压熔堆严重事故序列进行了分析研究。在假设未出现一回路稳压器安全阀开启后不回座、轴封冷却剂丧失事故，且操纵员开启二次侧SG大气释放阀尝试建立一回路自然循环冷却的情况下，全厂断电事故后16 361 s可能出现蠕变失效；自事故后16 610 s，SG传热管出现蠕变失效的可能性均远低于稳压器波动管与热管段，秦山二期核电厂全厂断电严重事故下因SG传热管蠕变失效而导致安全壳旁通的风险很小。

由于严重事故管理导则并非事故应急操作规程，严重事故的应对由技术支持中心(TSC)最终决策，本文对SG传热管蠕变失效风险的评价方法还可进一步结合轴封LOCA、稳压器安全阀卡开等过程研究，提供完整的用于评价SAG-1中传热管蠕变失效负面影响的风险指标，供TSC决策参考。

参考文献：

[1] NRC. Risk assessment of severe accident-induced steam generator tube rupture, NUREG-1570[R]. US: NRC, 1998.

[2] MAJUMDAR S. Prediction of structural integrity of steam generator tubes under severe accident conditions[J]. Nuclear Engineering and Design, 1999, 194(1): 31-55.

[3] LIAO Y, GUENTAY S. Potential steam generator tube rupture in the presence of severe accident thermal challenge and tube flaws due to foreign object wear[J]. Nuclear Engineering and Design, 2009, 239(6): 1 128-1 135.

[4] BANG Y, JUNG G, LEE B, et al. Estimation of temperature-induced reactor coolant system and steam generator tube creep rupture probability under high-pressure severe accident conditions[J]. Journal of Nuclear Science and Technology, 2012, 49(8): 857-866.

[5] PENG C H, YANG Y H. The analysis of severe accident induced steam generator tube rupture and LERF risk[J]. Advanced Materials Research, 2013, 614: 626-631.

[6] BANSAH C Y, AKAHO E H K, AYENSU A, et al. Theoretical model for predicting the relative timings of potential failures in steam generator tubes of a PWR during a severe accident[J]. Annals of Nuclear Energy, 2013, 59: 10-15.

[7] LARSON F R, MILLER J. A time-temperature relationship for rupture and creep stresses[J]. Trans ASME, 2008, 74: 765-775.

[8] 付霄华. SCDAP/RELAP5与MELCOR程序对堆芯损伤过程预测的比较[J]. 核动力工程,2003,24(5):430-434.

FU Xiaohua. Comparable simulations of PWR core damage progression by SCDAP/RELAP5 and MELCOR computer codes[J]. Nuclear Power Engineering, 2003, 24(5): 430-434(in Chinese).