饱和氢气加注过程中低温贮箱降温特性及热应力分布的数值研究
朱康,厉彦忠,2,王磊,文键,李翠
(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.航天低温推进剂技术国家重点实验室, 100028, 北京)
饱和氢气加注过程中低温贮箱降温特性及热应力分布的数值研究
朱康1,厉彦忠1,2,王磊1,文键1,李翠1
(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.航天低温推进剂技术国家重点实验室, 100028, 北京)
为了获得低温贮箱在饱和氢气加注过程中的降温特性以及箱体壁面的热应力分布,通过计算流体力学软件FLUENT计算了一定加注流量下贮箱内部流体区域的流场、温度场和壁面内的温度场变化,分析了加注过程中贮箱内的流动特性和降温特性;采用单向流固耦合方法进行壁面热应力分析,得到了3种不同进、出口约束条件下热应力在壁面中的分布以及最大热应力随时间的变化情况,并分析了进、出口弹性支撑约束条件设置的合理性;考虑贮箱内的压力变化,进行了箱体壁面的综合应力分析。计算结果表明:加注过程可以分为3个阶段,前2个阶段贮箱内部的流场、温度场和壁面温度分布特性依次由入口强制对流和壁面自然对流单独决定,第3阶段由入口强制对流及壁面自然对流共同决定;在3种不同的约束条件下,箱体壁面中的最大热应力均出现在贮箱加注口和排气口处,在进、出口弹性支撑条件下,壁面最大热应力随时间先增大而后趋于稳定,在稳定应力状态下,热应力的存在使箱体壁面总应力增加了15%左右。
液体火箭;低温贮箱;饱和氢气;低温加注;降温特性;热应力
随着航天事业的发展,对火箭运载能力的要求不断提高。我国的新型大推力火箭以液氢、液氧等低温流体作为推进剂,在发射前由地面装置完成推进剂的加注工作。低温贮箱等压力容器在工作过程中除了承受机械、压力等外部载荷产生的结构应力以外,还将承受热应力。热应力产生的主要原因是由温度变化导致的热变形受到了内部及外部约束条件的限制。如果箱体壁面中的最大应力超过了材料的屈服应力,就会产生严重的塑性变形,继而造成强度失效。因此,在设计低温贮箱时对壁面中可能产生的热应力进行分析显得至关重要。
国内外学者在热应力分析领域已经进行了广泛的研究。丁昌等介绍了ANSYS软件在低温压力容器应力分析中的应用[1],为低温压力容器设计提供了思路。刘占生等对超临界汽轮机高压缸进行了有限元热应力分析[2],为超临界机组的研究与开发提供了理论依据。朱鸿梅等对非磁性低温杜瓦的螺纹粘接接头在冷却过程中的瞬态热应力进行了有限元分析,计算结果表明冷却过程初期(10 s时刻)接头等效应力的峰值是冷却结束后的近1.5倍[3-4]。Kim、Kang等对纤维缠绕的复合材料/铝环状试件进行了低温下的热应力试验和有限元分析,结果表明,-150 ℃时在复合材料层中产生压应力,而在铝层中产生拉应力,应力值为屈服应力的32%[5-6]。低温环境下的结构热应力已经得到了一定程度的关注,然而薄壁低温容器在非稳态降温过程中的整体热应力分析尚未见报道。
本文首先通过计算流体力学(CFD)软件FLUENT计算了饱和氢气加注过程中低温箱体壁面的温度分布,然后采用单向流固耦合方法和有限元计算获得了箱体壁面中的热应力分布和变化情况,得出了热应力在较高压力低温贮箱综合应力中所占的比例,以期为低温贮箱气体加注过程的安全高效进行提供理论依据,并为低温贮箱液体加注过程相关研究的开展提供思路。
1 研究对象及建模
1.1 研究对象
以液体火箭液氢箱体为研究对象,如图1所示,上、下椭球形封头的长半径和短半径分别为4 250和2 656 mm,中间柱段长度为90 mm;贮箱加注口和排气口分别位于贮箱轴线的下端和上端,直径均为400 mm。结构材料为2219铝合金,壁面厚度为4 mm,壁面外侧覆盖了厚度为35 mm的保温层。初始时刻贮箱内部充满氦气,温度为300 K,箱内压力为微正压(0.11 MPa)。低温流体从贮箱加注口注入,冷却贮箱壁面及绝热层,同时导致箱内压力升高,当压力达到一定值(0.32 MPa)时排气口开始排气,阻止压力继续升高。
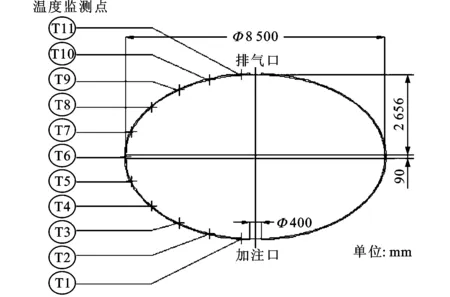
图1 低温贮箱结构及尺寸示意图
1.2 CFD数学模型
1.2.1 控制方程及网格模型 CFD计算区域包括流体区域和固体区域。在流体区域内开展流动、换热及两种气体混合的数值模拟,控制方程包括质量、动量、能量方程及组分传输方程;在固体区域开展固体导热模拟,控制方程只有能量方程。
考虑贮箱的对称性,以中轴线为旋转轴建立二维轴对称计算模型,如图2所示。
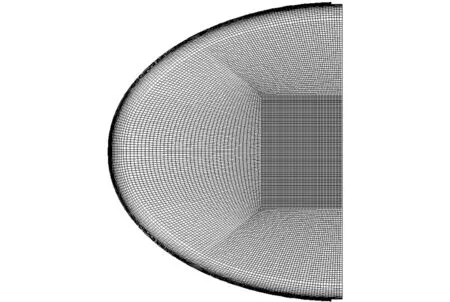
图2 液氢贮箱的二维轴对称CFD模型
1.2.2 边界条件及物性设置 在实际加注过程中,若供气压力保持不变,则随着贮箱压力的升高,入口处低温气体的密度将逐渐增大,而流速逐渐减小,逐渐增大的气体密度和逐渐减小的入口流速对入口质量流量的影响在一定程度上相互抵消。随后进入稳压过程,贮箱入口的质量流量保持不变。另外,升压过程在整个加注过程中所占的比例很小(约为1.2%),因此可将贮箱加注口设置为质量流量入口,给定入口的质量流量(2 kg/s)和流体温度(24.91 K)。
在贮箱升压阶段排气口封闭,当箱内压力达到一定值后排气口打开开始排气。因此,排气口在增压阶段是壁面边界,在稳压阶段则是出口边界。将贮箱排气口设定为速度入口边界条件,并将出口速度表示成出口压力的函数,通过用户自定义函数(UDF)植入计算程序中来控制出口速度的大小。
低温贮箱保温层外壁面设置为对流边界,环境温度设定为300 K,使用如下球体自然对流传热关联式[7]计算Nu,进而可求出外壁面换热系数
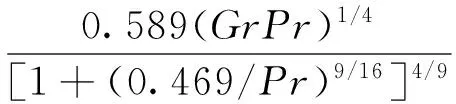
(1)
式中:Nu为努塞尔数;Gr为格拉晓夫数;Pr为普朗特数。
使用理想气体模型计算混合气体的密度。为了简化计算,同时考虑到其他物性在计算过程中的变化程度以及紊流的影响,将气体的导热系数、比定压热容、黏度、质量扩散系数以及铝合金、保温层的导热系数和比热容均设置为常数。
1.3 有限元结构分析模型
1.3.1 控制方程及节点模型 结构材料区域内的弹性力学控制方程包括平衡微分方程、几何方程以及物理方程。考虑贮箱结构的轴对称性,在经度方向取1°角对应的壁面区域建立结构分析的有限元模型。
本文通过剖析调研中的主要问题,给出了“集合的含义及其表示”这一节课新的教学设计,并提出了核心素养视角下概念教学的一些思考.
1.3.2 约束条件及力学性能参数设置 由贮箱的对称性可知,贮箱有限元模型中平行于径向的2个对称壁面在其法线方向上的位移为0,只能在其所在的平面内膨胀或收缩,可对这2个壁面施加FrictionlessSupport约束条件。为了给进、出口内壁面施加合理的约束条件,先考虑以下2种简单的情况:①进、出口没有法兰和管路等的径向支撑,内壁面可以在径向自由膨胀(收缩),此时进、出口内壁面无约束;②进、出口管路对贮箱进、出口内壁面有径向刚性支撑,则进、出口内壁面在径向的位移为0,相应施加FrictionlessSupport约束。实际情况应介于上述2种约束之间,即进、出口内壁面可以有一定的径向位移,但是不能自由膨胀(收缩),即管路或法兰对进、出口内壁面具有一定程度的弹性支撑,可对进、出口内壁面施加ElasticSupport约束条件。本文对上述3种情况均进行了有限元分析。
为了计算加注过程中箱体壁面内产生的热应力,将一系列不同时刻箱体壁面温度分布的CFD计算结果导入结构分析模块中。当只计算贮箱热应力分布而不考虑贮箱压力产生的外载应力时,贮箱内、外壁面均为自由边界;当考虑外载应力时,则在贮箱内、外壁面上施加压力边界条件。
将铝合金材料的泊松比、弹性模量及线膨胀系数设置为常数,数值分别为0.32、85GPa和1.2×10-6K-1[8-9]。
2 饱和氢气加注过程中低温贮箱的降温特性
为了展示加注过程中箱体壁面不同位置的温度变化情况,在箱体壁面上沿同一条经线布置一组温度监测点(图1中标“+”处,分别用T1~T11表示),用来监测各位置温度随时间的变化,结果见图3和和图4。
在加注过程中,贮箱固体区域和流体区域进行耦合传热,箱体壁面的降温特性由流体区域的流场及温度场决定。贮箱内的流场主要受到加注口入射强制对流和沿箱体内壁面形成的自然对流的影响,根据上述2种因素影响程度的不同,可以将加注过程分为以下3个阶段。
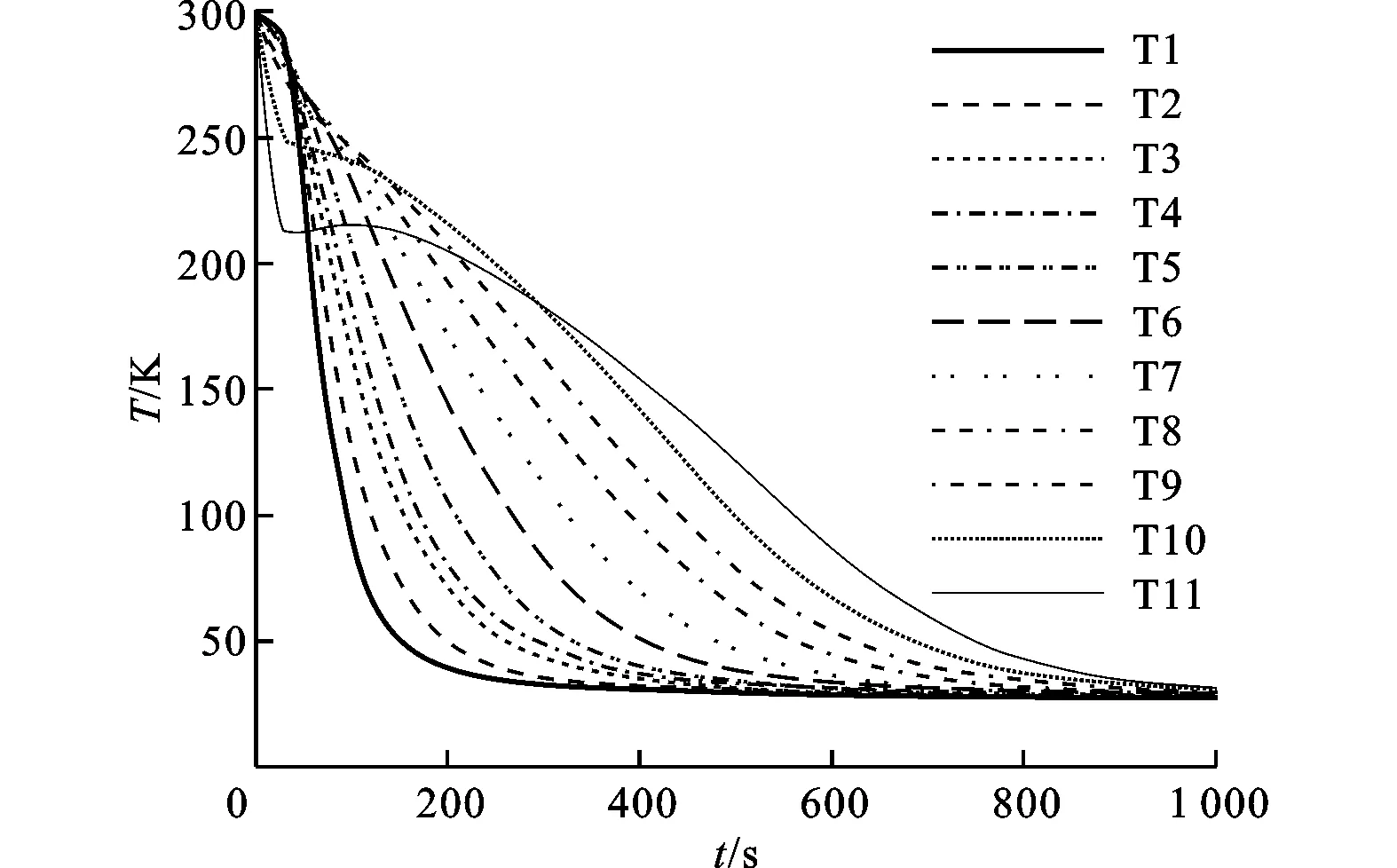
图3 箱体壁面不同位置的温度变化曲线(0~1 ks)
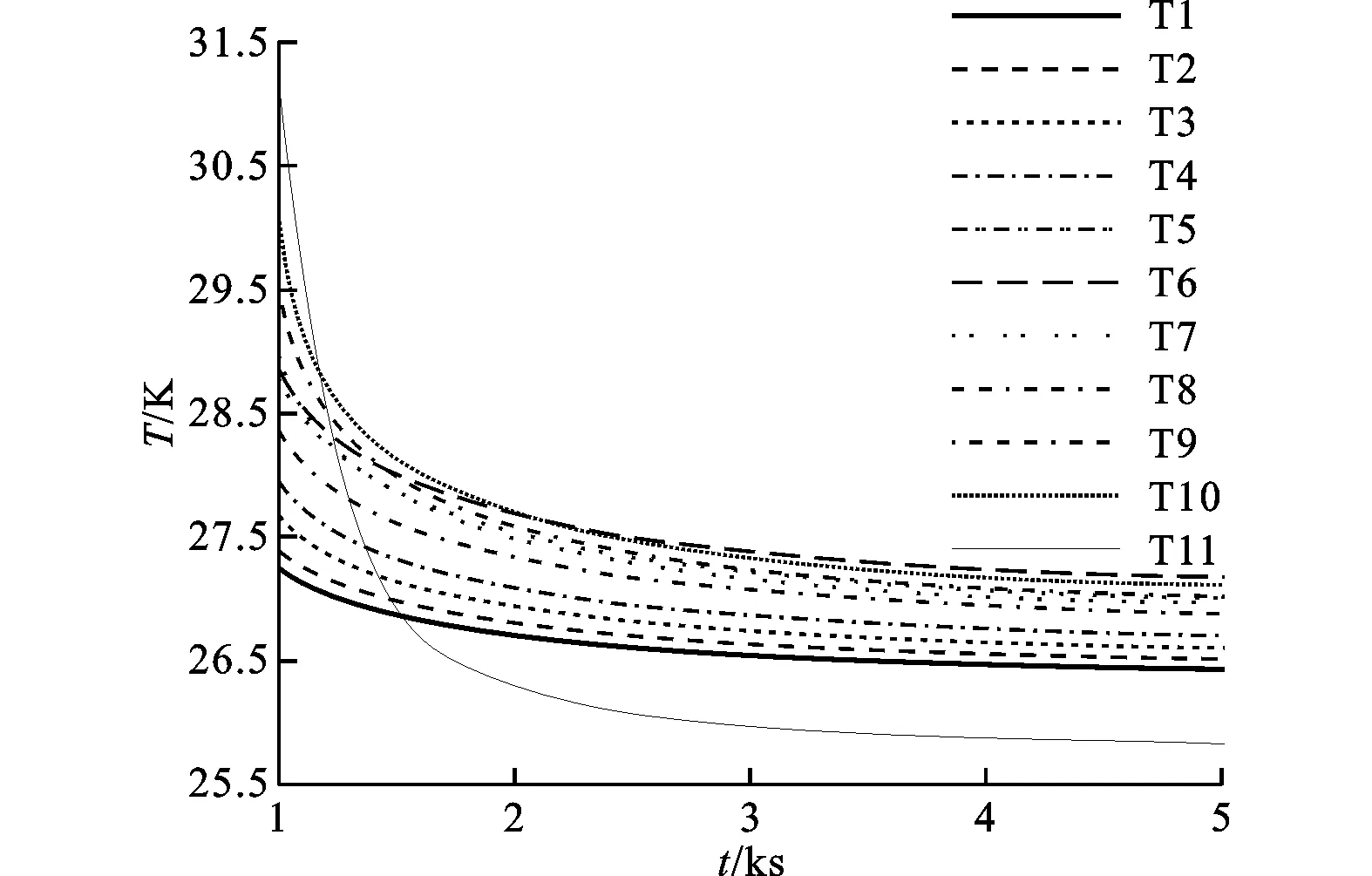
图4 箱体壁面不同位置的温度变化曲线(1~5 ks)
在第1阶段(0~20s),贮箱内压力较低,饱和氢气入口流速较大,低温气体直接上冲至位于贮箱上端的排气口,而后沿壁面向下流动,此阶段中贮箱内的流场主要受入口强制对流影响,自然对流尚未形成;排气口附近的壁面温降速率最大,沿壁面向下温降速率逐渐减小。从图3中可以看到,在加注过程初期,壁面温度从上到下逐渐升高。图5展示了10s时刻贮箱内的流场和温度场分布情况。
在第2阶段(20~1 000s),随着贮箱内压力的升高,入口流速相应减小,入流低温氢气不能冲至排气口,而是上冲至一定高度后在重力和浮力的综合作用下向贮箱下部流动,并与常温氦气混合。处在贮箱下部的低温气体在壁面的加热下密度减小,在浮升力作用下沿壁面向上流动,形成自然对流。图6展示了200s时刻贮箱内的流场和温度场分布情况,图7展示了加注过程中贮箱内部压力随时间的变化情况。由图7可知,加注过程进行至60s时贮箱内部压力达到稳定值。在此阶段,壁面降温速率沿壁面向上逐渐减小,壁面温度沿壁面向上逐渐升高,前2个阶段之间有一个明显的过渡,见图3。
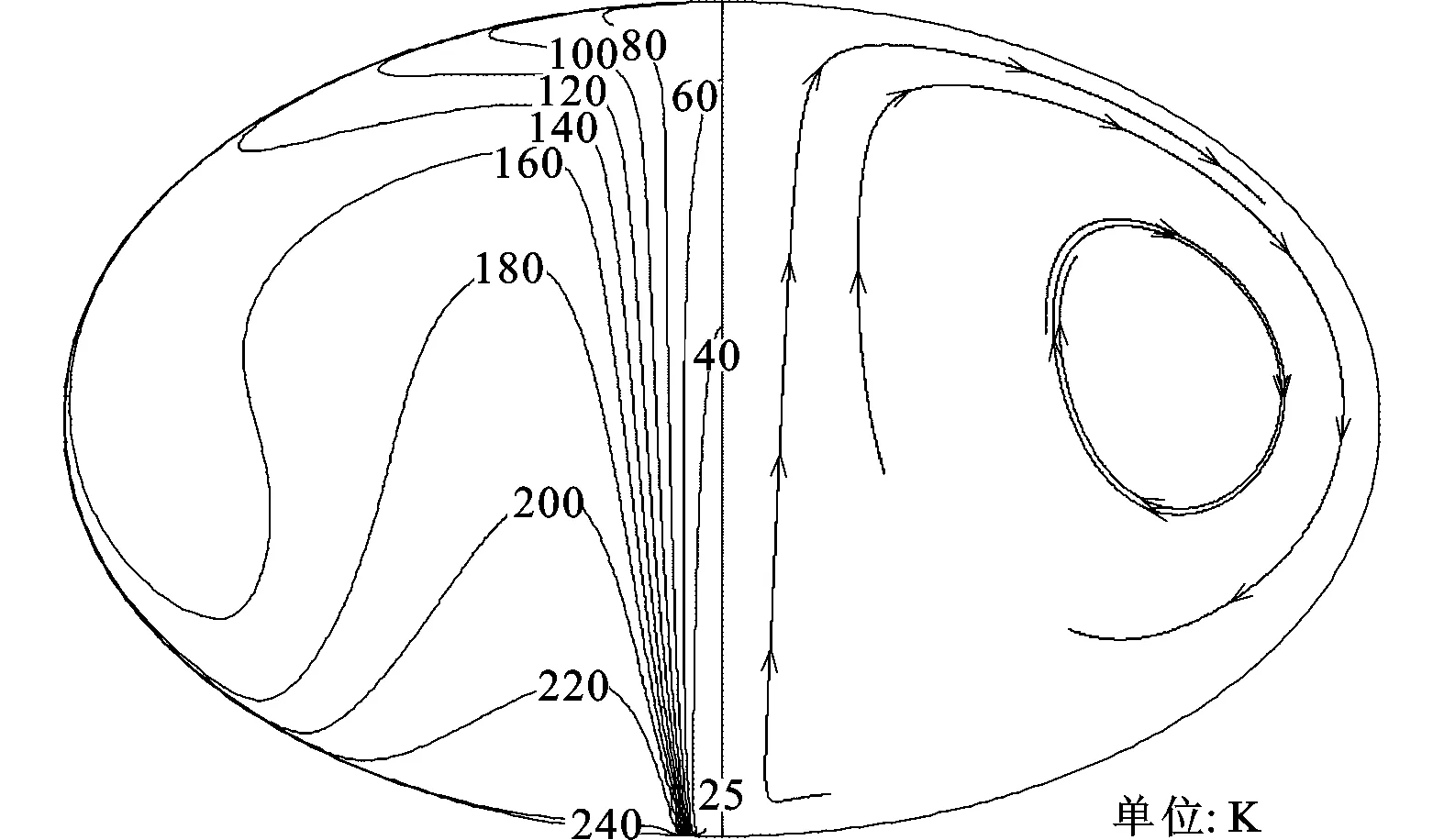
图5 第1阶段10 s时贮箱内的温度场及流场分布
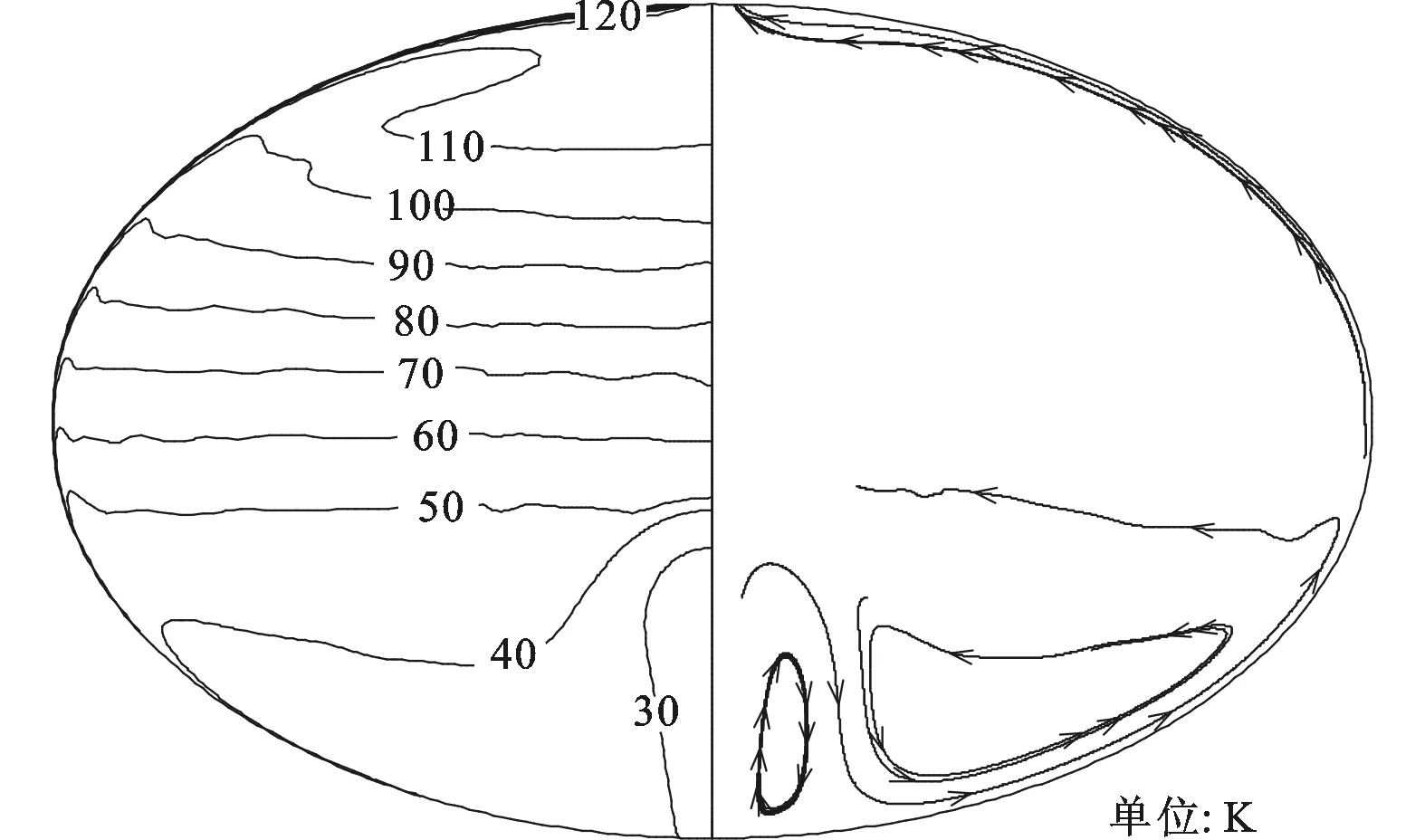
图6 第2阶段200 s时贮箱内的温度场及流场分布
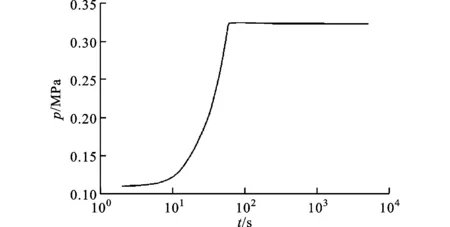
图7 加注过程中贮箱内部压力随时间的变化情况
在第3阶段(1~5ks),随着贮箱内整体温度的降低,箱内气体密度逐渐增大,入流气体受到的浮力增大,能够达到的垂直高度相应升高,在加注过程进行到一定程度后入流气体重新上冲至排气口。由于此时排气口打开,所以上冲的部分低温气体直接排出贮箱,此阶段壁面自然对流和入口强制对流各自独立地影响贮箱内的流场,图8展示了2ks时刻贮箱内的流场和温度场分布情况。总体上说,壁面温度沿壁面向上逐渐升高,而排气口附近的壁面由于低温气体的冲刷,温度处于最低,如图4所示。
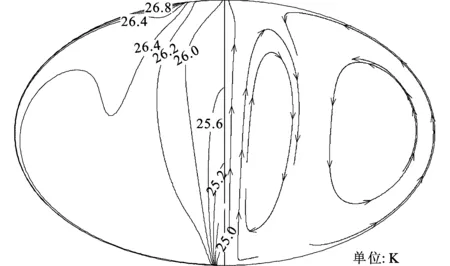
图8 第3阶段2 ks时贮箱内的温度场及流场分布
3 饱和氢气加注过程中低温箱体壁面的热应力分析
3.1.1 箱体壁面热应力空间整体分布情况 为了获得箱体壁面热应力的分布情况,先不考虑贮箱内压力产生的外载应力,只对变温导致的热应力进行分析计算。分析发现,无论在进、出口处采用何种约束条件,贮箱的最大热应力始终出现在进口和出口处,其他位置的热应力很小。出现这种分布规律与热应力的性质有关。材料中的应力可以分为一次应力、二次应力和峰值应力等[10],其中二次应力是由于热胀冷缩、端点位移等位移载荷的作用而产生的应力,不直接与外力平衡,是为满足位移约束条件或自身变形的连续性要求所需的应力。二次应力的特点是自限性和局部性,即局部屈服或小量变形就可以使位移约束条件或自身连续性要求得到满足,此后变形不再继续增大。热应力属于二次应力,因此在本文的研究对象中只在位移约束条件附近存在明显的应力。
3.1.2 进出口无径向约束条件下的贮箱热应力分布 根据塑性材料的第三强度理论和第四强度理论,对箱体壁面的最大剪应力和vonMises等效应力进行考察和对比分析。在进、出口内壁面无径向约束条件下,箱体壁面的最大热应力以及进、出口内壁面的径向位移随时间的变化情况如图9、图10所示,其中下角标M表示vonMises等效应力,s表示最大切应力,in表示入口,out表示出口。从图9可以看出,在加注过程初期壁面最大应力逐渐升高,达到峰值(vonMises等效应力为12.81MPa,最大切应力为6.44MPa)后开始减小,之后的变化过程相对比较平缓。为了便于分析壁面最大热应力的变化及其在进、出口位置之间的转换,分别将贮箱进口和出口处的vonMises等效应力随时间的变化情况示于图11中,最大切应力的变化趋势与等效应力大致相同,图中没有示出。
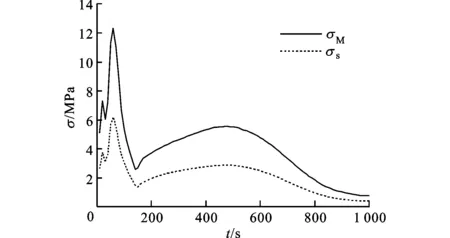
图9 进出口无径向约束时的最大热应力变化曲线
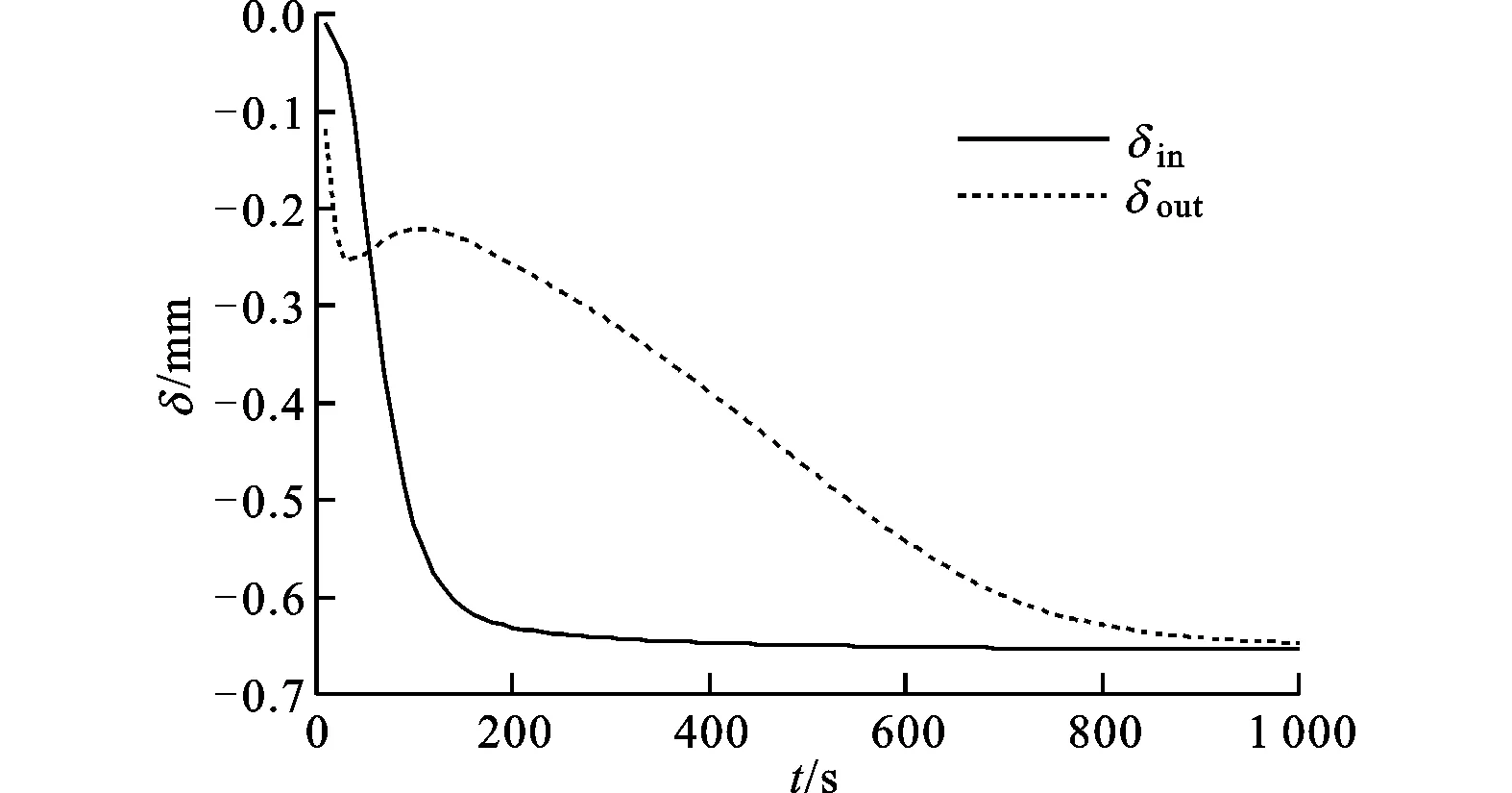
图10 进出口内壁面径向位移的变化曲线
热应力的大小与相应位置的温度梯度有关。在贮箱下部,加注过程初始阶段进口处温降速率逐渐增大,进口附近的温度梯度和热应力相应增大;随着加注过程的进行,壁面温度梯度逐渐减小,热应力随之减小并趋于稳定。在贮箱上部,加注过程初始阶段低温气体直接冲刷出口位置,出口温降速率较大,因此热应力较大;随着箱内压力的升高和低温气体进口速度的减小,出口位置的温降速率减小,导致温度梯度减小,因此热应力也相应减小;之后出口位置的温度逐渐高于其他位置,温度梯度改变方向且数值增大,热应力相应增大,在500s左右出现的较小热应力峰值与温度梯度的这一改变相吻合。加注过程后期整个箱体的温度趋于进口低温气体的温度,出口处温度梯度逐渐减小,热应力减小并趋于稳定。由于进、出口内壁面没有径向约束,温度降低时可以自由收缩,因此相对于有径向约束的情况,壁面应力比较小,而壁面位移量比较大。图12展示了箱体壁面最大位移量的变化曲线。
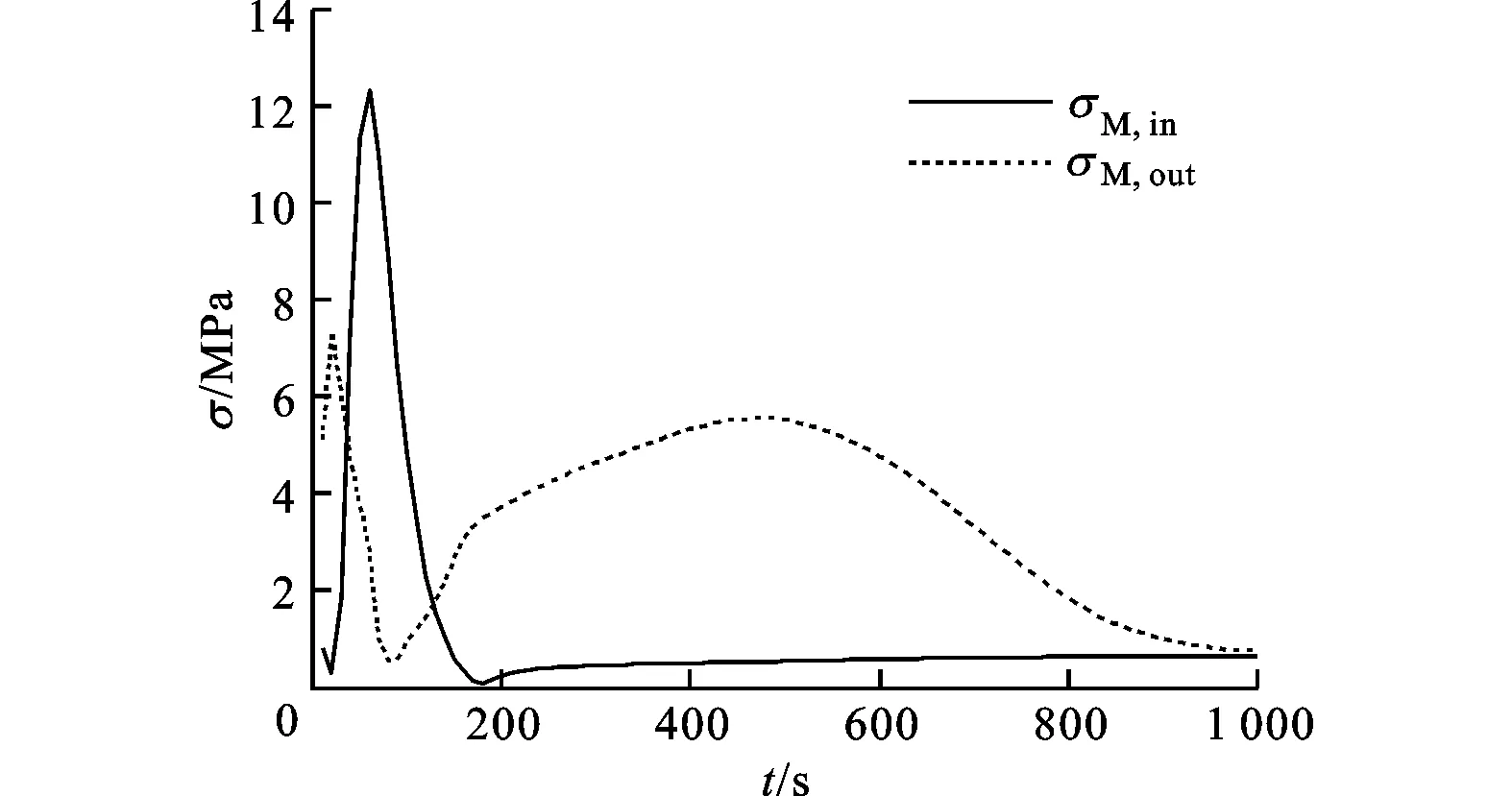
图11 无径向约束时进出口von Mises应力的变化曲线
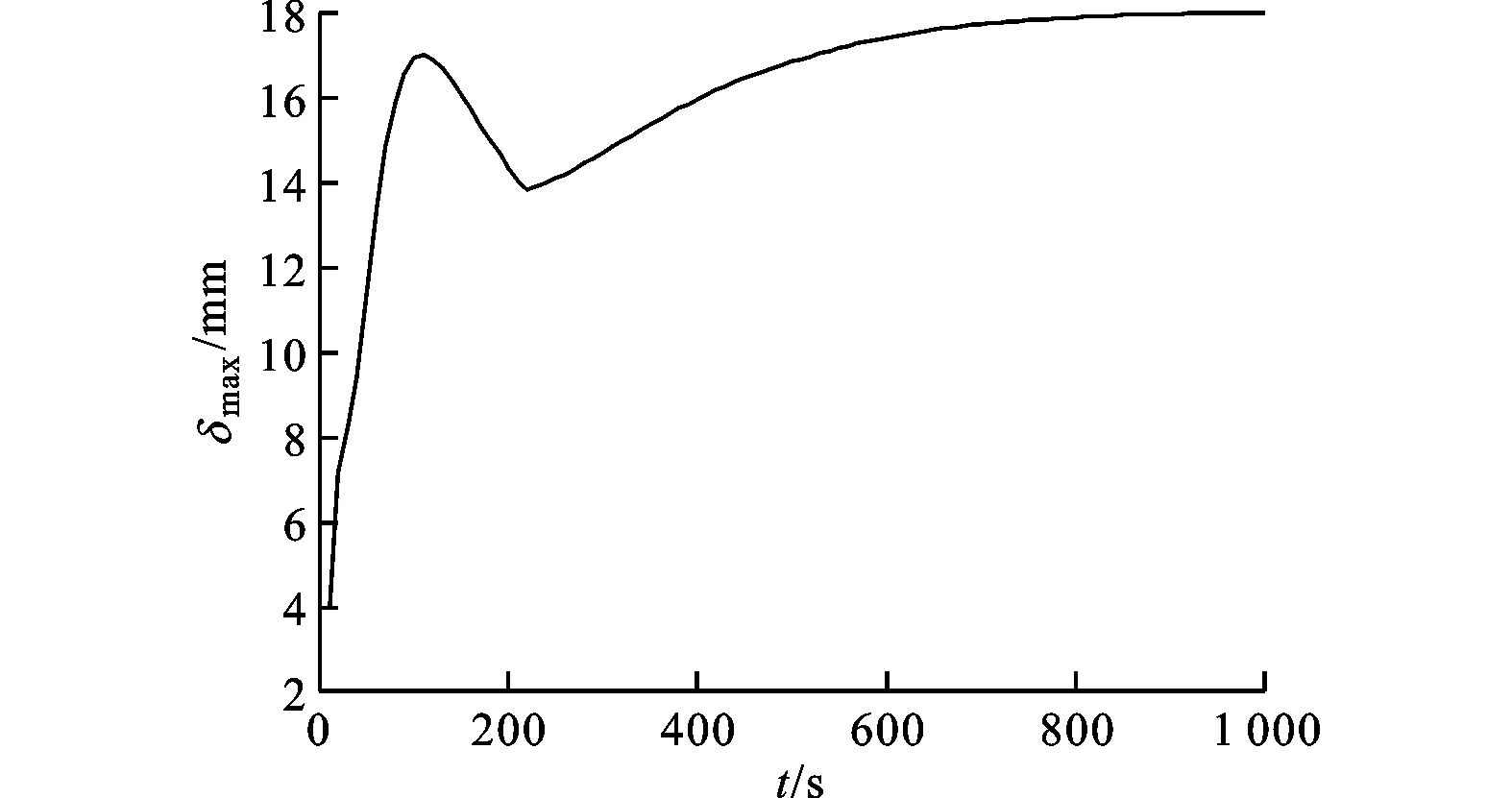
图12 箱体壁面最大位移量变化曲线
3.1.3 进出口有径向刚性约束条件下的贮箱热应力分布 在进、出口内壁面有径向刚性约束条件下,箱体壁面的最大热应力随时间的变化情况如图13所示。从图中可以看出,壁面最大热应力随着加注过程的进行先增大而后逐渐稳定(vonMises等效应力为514.84MPa,最大切应力为285.97MPa)。进、出口内壁面径向刚性约束条件下的壁面最大热应力比无径向约束下的值大了1个量级,这是因为进、出口内壁面的径向刚性约束完全限制了相应位置的径向变形,使得该处产生较大的应力。进、出口内壁面的径向位移量(见图10)越大,刚性约束的约束力就越强,产生的应力也越大,因此刚性约束条件下进、出口处的热应力总体先增大而后逐渐稳定,其中出口热应力在加注初期有一段短暂的降低,如图14所示,对应于图3和图10中相应时间出口壁面温度的升高和径向位移绝对值的减小。贮箱变形稳定后,壁面相对于初始位置的最大位移量为14mm,与图12对比可知,径向刚性约束下的壁面位移量小于无径向约束的情况。
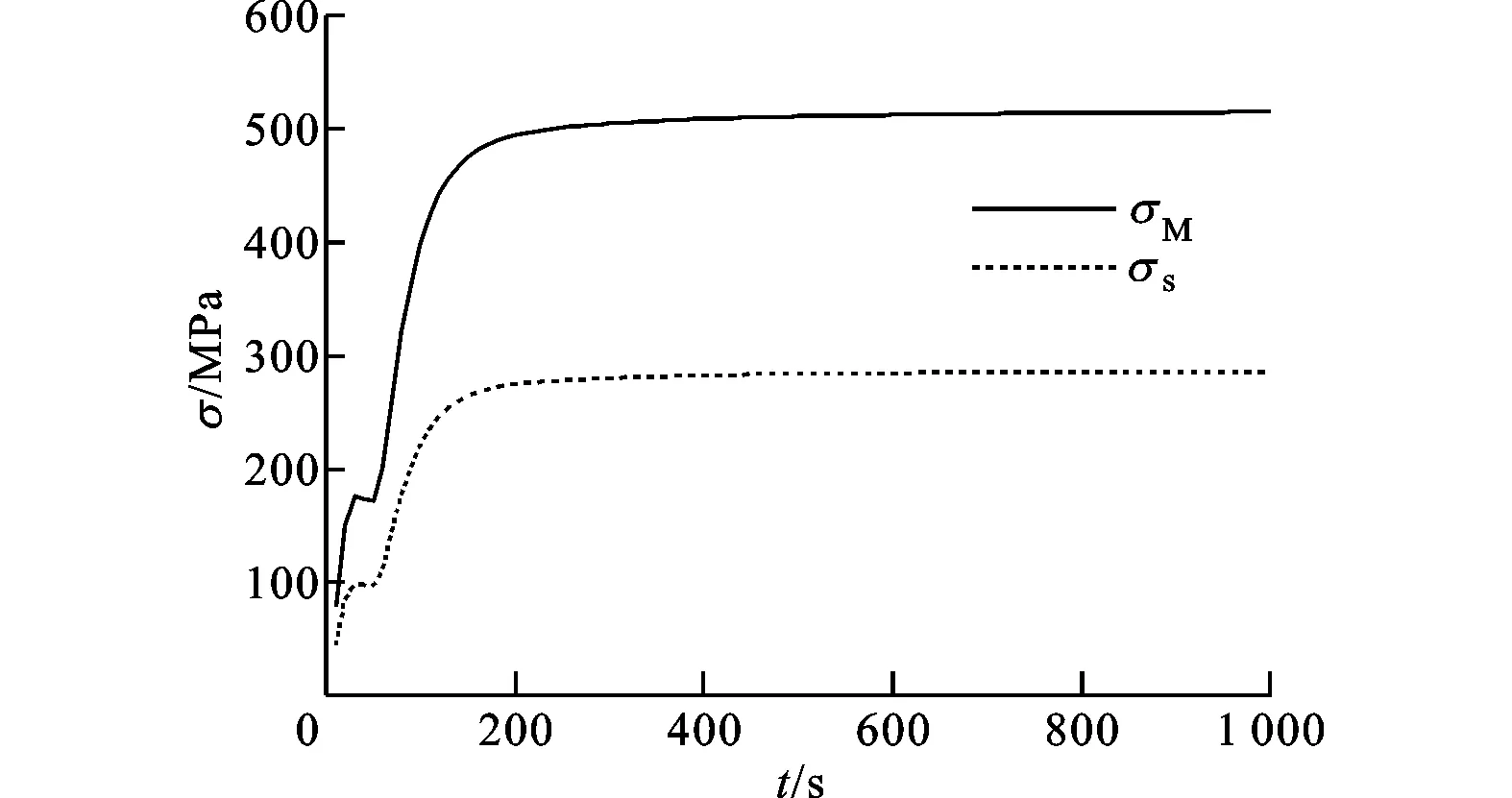
图13 进出口内壁面有径向刚性约束时壁面的最大热应力变化曲线
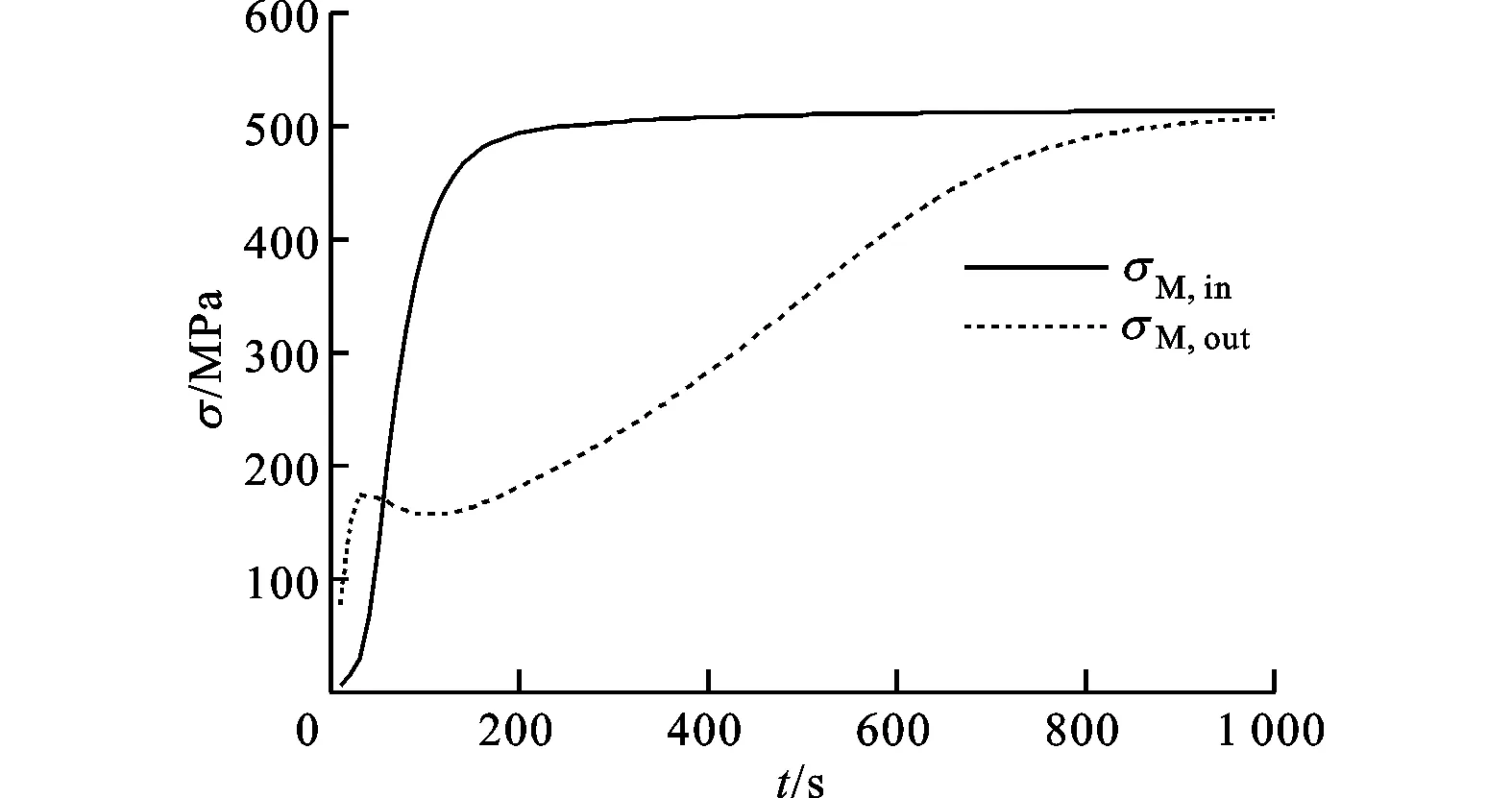
图14 进出口处von Mises应力的变化曲线
3.1.4 进出口有径向弹性支撑条件下的贮箱热应力分布 在弹性支撑约束条件下,进出口内壁面在径向可以有一定的位移。要计算径向位移,就需要给定弹性支撑的刚度(N/m3),即支撑方向单位位移所产生的应力。假设与内壁接触的是外径为400mm、壁厚为5mm的不锈钢管,使用ANSYS的静态结构分析模块,在给定管路外壁径向位移为-1mm的条件下进行应力分析,得到外壁的径向压应力为28.776MPa,因此贮箱进、出口弹性支撑的刚度为28.776GN/m3。
将以上得到的刚度数值输入贮箱结构分析的弹性支撑约束条件中,得到进、出口有径向弹性支撑时箱体壁面最大热应力随时间的变化情况,发现其变化趋势与进、出口有径向刚性约束条件时的情况相同。与进、出口有径向刚性约束的情况相比,由于允许进、出口产生一定的径向位移,因此进、出口处的局部变形得到缓解,箱体壁面的最大应力明显降低,由温差导致的变形逐渐稳定后,壁面的最大vonMises等效应力稳定在78.19MPa,最大切应力稳定在42.12MPa。弹性支撑条件下进、出口内壁面径向位移的变化趋势与无径向约束条件下的相同,径向位移量最大值分别为0.526和0.521mm,小于无径向约束条件下对应的数值(0.654和0.648mm),直观地体现出了弹性支撑的径向约束作用。
参考不锈钢管弹性支撑的刚度数值,分别减小和增大10个量级,将弹性支撑的刚度分别设定为1(刚度很小)和1020(刚度很大),再进行贮箱热应力分析,得到的箱体壁面变形及应力分布分别与无径向约束及有径向刚性约束条件下的结果相同,说明无径向约束和有径向刚性约束分别是弹性支撑的2种极端情况,证明了约束条件设置的合理性。
3.2 考虑箱内压力的贮箱综合应力分析
在低温气体加注过程中,贮箱内逐渐形成稳定的压力场,由于箱内充满了低密度气体,不同位置的压力相差不大,因此进行应力分析时可以认为贮箱不同位置所受的压力均为出口压力。将不同分析时刻的出口压力施加到贮箱内壁,在贮箱外壁施加1个大气压,结合不同时刻的温度数据对贮箱进行结构分析,得到了贮箱壁面最大等效应力随时间的变化情况,如图15所示。为了分析热应力对贮箱总应力的影响,将由压力单独引起的壁面最大应力也示于图中,下角标t表示综合应力,p表示压力产生的应力。在外载应力的基础上考虑热应力时,壁面最大等效应力从323.64增加到378.36MPa,增加了16.91%;最大切应力的变化趋势与等效应力的变化趋势相同,数值从167.56增加到189.43MPa,增加了13.05%。

图15 进出口有径向弹性支撑时贮箱综合等效应力及外载等效应力的变化曲线
4 结 论
本文使用ANSYS软件进行了饱和氢气加注过程中低温贮箱降温过程的数值模拟,并对箱体壁面的热应力进行了有限元分析,得到以下结论。
(1)在文中给定的加注流量(2kg/s)下,低温贮箱降温过程经历了3个阶段,不同的流场特性导致了不同的壁面降温特性:第1阶段箱内流场主要由入口强制对流决定,壁面温度从上到下逐渐升高;第2阶段箱内流场主要由壁面自然对流决定,壁面温度从下到上逐渐升高;第3阶段箱内流场由入口强制对流和壁面自然对流共同决定,排气口附近温度最低,其他壁面区域温度从下到上逐渐升高。
(2)在3种不同的进出口约束条件下,箱体壁面的最大热应力均出现在加注口和排气口处。在进、出口无径向约束条件下,最大热应力随时间先增大后降低;在进、出口有径向刚性约束及弹性约束条件下,最大热应力随时间先增大而后逐渐稳定。在无径向约束条件下,进、出口的径向位移最大而热应力最小;在有径向刚性约束条件下,进、出口无径向位移且热应力最大;在有径向弹性约束条件下,进、出口的径向位移和热应力均处于前述2种约束条件的结果之间。在实际情况下贮箱进、出口会受到径向弹性支撑,进、出口无径向约束和有径向刚性约束是2种极端约束情况。
(3)在文中给定的进、出口径向弹性支撑条件下,箱体壁面中的最大热应力占相应位置处贮箱总应力的15%左右。
[1] 丁昌, 汪荣顺. ANSYS在低温压力容器应力分析与优化设计中的应用 [J]. 低温与超导, 2007, 35(6): 455-457. DING Chang, WANG Rongshun. Application of ANSYS in stress analysis and optimization design of cryogenic pressure vessels [J]. Cryogenics and Superconductivity, 2007, 35(6): 455-457.
[2] 刘占生, 顾卫东, 朱自民, 等. 超临界汽轮机高压缸有限元热应力分析 [J]. 汽轮机技术, 2002(2): 23-25. LIU Zhansheng, GU Weidong, ZHU Zimin, et al. Thermal stress analysis of finite element method of high pressure cylinder of supercritical 600 MW turbine [J]. Turbine Technology, 2002(2): 23-25.
[3] 朱鸿梅, 徐烈, 孙恒, 等. 低温粘接技术的应用及热应力分析 [J]. 低温与超导, 2004, 32(2): 29-30. ZHU Hongmei, XU Lie, SUN Heng, et al. The application and thermal stress analysis of cryogenic adhesive bonding technology [J]. Cryogenics and Superconductivity, 2004, 32(2): 29-30.
[4] ZHU Hongmei, SUN Heng, XU Lie, et al. Transient thermal stress analysis of threaded-adhesive joints applied in non-magnetic Dewar [J]. International Journal of Adhesion & Adhesives, 2007, 27(8): 621-628.
[5] KIM M G, KANG S G, KIM C G, et al. Thermally induced stress analysis of composite/aluminum ring specimens at cryogenic temperature [J]. Composites Science and Technology, 2008, 68(3): 1080-1087.
[6] KANG S G, KIM M G, KIM C G, et al. Thermo elastic analysis of a type 3 cryogenic tank considering curing temperature and autofrettage pressure [J]. Journal of Reinforced Plastics and Composites, 2008, 27(5): 459-471.
[7] 杨世铭, 陶文铨. 传热学 [M]. 北京: 高等教育出版社, 2006: 269-270.
[8] HATCH J E. Aluminum: properties and physical metallurgy [M]. Metals Park, Ohio, USA: American Society for Metals, 1984: 6.
[9] DAVIS J R. Aluminum and aluminum alloys [M]. Geauga County, Ohio, USA: ASM International, 1993: 69.
[10]秦叔经. 应力分类概念在压力容器设计中的应用 [J]. 化工设备与管道, 2001, 38(5): 5-11. QIN Shujing. The application of stress classification in the design of pressure vessels [J]. Process Equipment and Piping, 2001, 38(5): 5-11.
(编辑 葛赵青 荆树蓉)
InvestigationonCool-DownBehaviorandThermalStressofCryogenicTankDuringSaturatedHydrogenGasFillingProcess
ZHU Kang1,LI Yanzhong1,2,WANG Lei1,WEN Jian1,LI Cui1
(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028, China)
A numerical study is performed on the cool-down behavior and thermal stress of a cryogenic tank during the saturated hydrogen gas filling process. CFD simulation is carried out to obtain the flow and temperature distributions inside the tank and the temperature distribution of the tank wall under a specific filling rate. Then the flow and cooling characteristics of the tank during the filling process are analyzed. The thermal stress in the tank wall under three different constraints of the inlet and outlet is calculated with unidirectional fluid-solid coupling method, and the spatial distribution and transient behavior of the thermal stress are revealed. In addition, the rationality of applying elastic supports to the inlet and outlet is demonstrated, and the integrated stress in the tank wall is calculated with the pressure variation in the tank taken into account. Numerical results show that the filling process can be divided into three steps, where the flow and temperature distributions inside the tank are governed by the forced convection from the inlet or the natural convection near the wall in the first and second steps, and by both of them in the third step. The maximum thermal stress appears at the inlet and outlet of the tank under any of the three constraints. For radial elastic support on the inlet and outlet, the maximum thermal stress increases gradually to a steady value and takes up about 15% of the maximum integrated stress in steady state.
liquid rocket; cryogenic tank; saturated hydrogen gas; cryogenic filling; cool-down behavior; thermal stress
10.7652/xjtuxb201405001
2013-11-21。 作者简介: 朱康(1990—),男,博士生;厉彦忠(通信作者),男,教授,博士生导师。 基金项目: 国家自然科学基金资助项目(51376142);教育部高等学校博士学科点专项科研基金资助项目(20100201110012);航天低温推进剂技术国家重点实验室基金资助项目(SKLTSCP1213);中国博士后科学基金资助项目(2013M532041)。
时间: 2014-03-05 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140305.1118.004.html
TK121
:A
:0253-987X(2014)05-0001-07

