拓展目标量测集合分割算法

闫小喜,韩崇昭,李威,连峰

(1.江苏大学电气信息工程学院, 212013, 江苏镇江; 2.西安交通大学电子与信息工程学院, 710049, 西安)

拓展目标量测集合分割算法

闫小喜1,韩崇昭2,李威2,连峰2

(1.江苏大学电气信息工程学院, 212013, 江苏镇江; 2.西安交通大学电子与信息工程学院, 710049, 西安)

针对拓展目标概率假设密度滤波器采用的量测集合所有可能分割方式在实际中几乎不能够实现的问题,提出了一种采用有限混合模型的量测集合近似分割算法,对所有可能分割方式进行近似处理。算法利用有限混合模型拟合量测集合以实现对量测集合的分割,首先利用期望极大化算法极大似然估计混合参数,然后利用量测来源的条件概率分割量测集合,最后以二维场景为例进行了仿真实验。仿真结果表明:新算法在所有时刻上的最优子模式分配和混合分量数目均小于现有的典型量测集合分割算法;在拓展目标跟踪性能上,新算法具有更好的多拓展目标跟踪性能。

拓展目标跟踪;概率假设密度;量测集合分割;有限混合模型

目标跟踪主要解决从目标量测和杂波中估计目标数目和目标状态的问题。目前,绝大多数目标跟踪算法是在“每个目标在一个时刻至多产生一个量测”的前提假设下建立起来的,即把目标简化为一个质点[1-3]。已有点目标跟踪算法大部分是基于数据关联的,需要建立起目标与量测的对应关系,此类方法是利用分散策略解决目标跟踪问题。近几年出现了利用整体策略的跟踪算法,即概率假设密度点目标跟踪算法[4-12]。然而,随着现代雷达系统分辨率的不断提高,尤其是高分辨率雷达和相控阵雷达的出现,雷达距离向分辨单元一般小于目标尺寸,一个雷达目标通常具有多个散射中心,该多散射中心特性体现在量测上为“每个目标在每个时刻产生多个量测”。因此,基于“每个目标在一个时刻至多产生一个量测”的点目标跟踪算法不再适合现代雷达系统,在“每个目标在每个时刻产生多个量测”情况下的目标跟踪应当视为拓展目标跟踪[13]。对于特定约束条件下的单拓展目标,已有粗略的序贯蒙特卡罗实现方法[14-15]和Bayesian实现方法[16-17]。对于一般情况下的拓展目标跟踪问题,一直缺乏严密的解决策略,直到拓展目标概率假设密度滤波器的出现[18]。拓展目标概率假设密度滤波器从概率假设密度的整体角度解决拓展目标状态估计问题,避免了数据关联环节。在拓展目标线性高斯假设下,可以利用加权高斯混合分量实现拓展目标概率假设密度滤波器[19]。

在拓展目标概率假设密度滤波器的高斯混合实现的步骤中,对量测集合的分割步占据着重要的地位,决定了整个实现算法的混合分量数目,从而决定了整个实现算法的拓展目标状态估计性能。然而,拓展目标概率假设密度滤波器用到的是量测集合的所有可能分割方式,在实际应用时,所有可能分割方式几乎是不能够实现的,需要对其进行近似处理。针对该问题,提出了一种基于有限混合模型的量测集合近似分割算法。

1 问题描述

拓展目标概率假设密度滤波器的预测步为

(1)

式中:vk|k-1是时刻k预测目标强度;pS,k是存活概率;fk|k-1是状态转移密度;vk-1是时刻k-1目标强度;βk|k-1是衍生转移密度;γk是出生强度。

拓展目标概率假设密度滤波器更新步[18]为

vk|k(x)=LZk(x)vk|k-1(x)

(2)

伪量测似然

LZk(x)=1-(1-e-λ(x))PD(x)+

(3)

式中:λ(x)是拓展目标期望量测数;PD是检测概率;p∠Zk是对量测集合Zk的分割;ωp是量测集合方式p在所有可能分割方式中所占的比重;W是量测分割单元;|W|是分割单元W中量测的数目;φz(x)=φ(z|x)是单量测似然;λc是期望杂波数目;ck(z)是杂波分布;分割单元因子

dW=δ|W|,1+

(4)

其中δ是Kronecker delta函数。

预测目标强度vk|k-1关于函数h(x)的复合强度函数定义为

(5)

与点目标概率假设密度滤波器高斯混合实现算法类似[11],拓展目标概率假设密度滤波器在拓展目标线性高斯假设条件下具有高斯混合实现形式,该实现形式利用高斯混合近似拓展目标概率假设密度[19]。该高斯混合实现算法主要包括预测高斯混合实现步、量测集合分割步、更新高斯混合实现步、混合分量删减步和状态提取步。式(3)对拓展目标概率假设密度的更新分为3个层次来实现:第1层次是量测集合分割层p∠Zk;第2层次是量测集合分割单元层W∈p;第3层次是单独量测层z∈W。其中,第1层次p∠Zk所表示的对量测集合Zk的分割,决定着第2层次和第3层次,是整个高斯混合实现算法中至关重要的一步,决定了整个高斯混合实现算法的混合分量数目、算法精度和时间开销。从式(3)关于p∠Zk的求和运算可以看出,此步是利用量测集合Zk的所有可能分割方式更新拓展目标概率假设密度。由于所有可能分割方式数目随着量测数目的增长而呈组合爆炸式增长,所以在具体实现中很难实现所有可能分割方式,即使对量测数目较少的量测集合Zk勉强实现所有可能分割方式,也会引入数目众多的混合分量,导致较大的时间开销,使整个高斯混合实现算法失去意义。因此,在拓展目标概率假设密度滤波器高斯混合实现中,需要对量测集合的所有可能分割方式进行近似处理,使得整个算法具有可行性。

2 算 法

如问题描述部分所述,我们的目的是对量测集合Z进行近似分割(为了简单,此部分省略量测集合Zk的下标k)。首先明确此处对拓展目标量测集合Z分割的基本要求:

(1)每一量测集合分割方式p∠Z中量测分割单元W非空;

(2)每一量测集合分割方式p∠Z中量测z所归属量测分割单元W唯一;

(3)每一量测集合分割方式p∠Z中量测分割单元W内量测z无序。

所提基于有限混合模型的量测集合近似分割算法,依据拓展目标的一个基本事实:每个拓展目标所产生的多量测分布在拓展目标附近,属于同一拓展目标的量测在空间上相距较近,不属于同一个拓展目标的量测在空间上相距较远。以此基本事实为出发点,所提算法利用有限混合模型拟合拓展目标量测集合以实现对量测集合的分割,使由同一拓展目标所产生的多个量测能够分割在同一量测分割单元中。具体来说,有限混合模型的拟合过程为量测集合的分割过程,拟合后每个混合分量对应一个量测分割单元,即拟合后混合分量数目等于量测集合分割单元数。每个量测根据其来自于混合分量的来源指示条件概率判断其量测分割单元的归属:选择量测的最大来源指示条件概率所对应的混合分量作为该量测的归属分割单元。

对量测集合Z={z1,…,zn},利用具有m混合分量的有限混合模型p(z|θ)进行拟合。该有限混合模型为

(6)

式中:πj表示分量j的混合权重;θj={μj,Cj}表示由均值μj和方差Cj构成的分量j的参数集合;θ={π1,…,πm,θ1,…,θm}表示整个有限混合模型的参数集合,有限混合模型的混合权重π1,…,πm满足

(7)

量测集合Z={z1,…,zn}的对数似然

(8)

所提算法采用极大似然方式分割量测集合,极大似然估计混合模型参数为

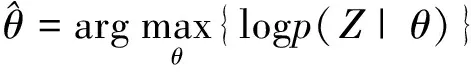
(9)

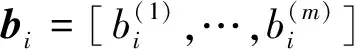
(10)

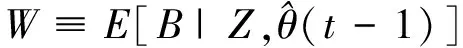
(11)

式中:t为期望极大化算法的迭代次数。W插入完全对数似然logp(Z,B|θ)后所构成的品质函数为

(12)

式中条件期望W的元素

(13)

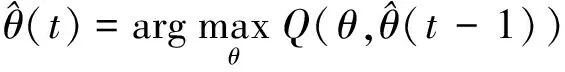
(14)

式(14)对有限混合模型参数的更新包括对混合权重的更新、对分量均值的更新和对分量方差的更新。关于混合权重的更新,算法采用与文献[20]类似的更新方式

(15)

式中:N表示用于描述每个混合分量的参数元素数目。在式(15)中,通过混合权重的置零操作来实现对具有负混合权重的混合分量的删减。对经式(15)更新后的所有非零混合权重进行正规化,调整量测集合Z={z1,…,zn}在各混合分量间的证据分配。经式(15)更新后,非零混合权重所对应的混合分量的均值μj和方差Cj的更新方式为

(16)

(17)

此处混合分量均值和方差的更新方式与文献[21]类似。

在算法起始步,需用较多数目的混合分量初始化有限混合模型(即初始化时混合分量数目m较大),以提高有限混合模型对量测集合的覆盖程度。

3 仿真实验

下面,以二维场景[-1000,1000]×[-1000,1000]为例来证明所提基于有限混合模型的量测集合分割算法的优势。拓展目标运动模型为

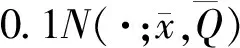
拓展目标单量测方程为

式中:量测噪声[w1,k,w2,k]T是零均值高斯白噪声,其分量标准差σw1=σw2=20m。与文献[19]中针对高分辨率雷达的拓展目标跟踪方法所取参数一致,每个拓展目标在每个时刻产生的量测数目服从参数为10的泊松分布,杂波数目服从参数为50的泊松分布,杂波在跟踪场景内均匀分布,检测概率为0.99。

算法在有限混合模型初始化时,取混合分量数目为50,混合参数迭代估计过程的终止条件为完全对数似然的相对变化率低于10-4。

在一次蒙特卡罗实验中,x坐标和y坐标的拓展目标真实值和算法估计值分别显示在图1和图2中。结果表明,所提量测集合分割算法在拓展目标高斯混合实现中能够正确估计多拓展目标状态,并能够识别拓展目标的出生和衍生。

图1 x坐标的估计值与真实值

图2 y坐标的估计值与真实值

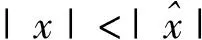
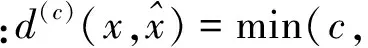
两种算法混合分量数目的对比如图4所示,可以看出,所提量测集合分割算法的混合分量数目小于典型量测集合分割算法的数目。

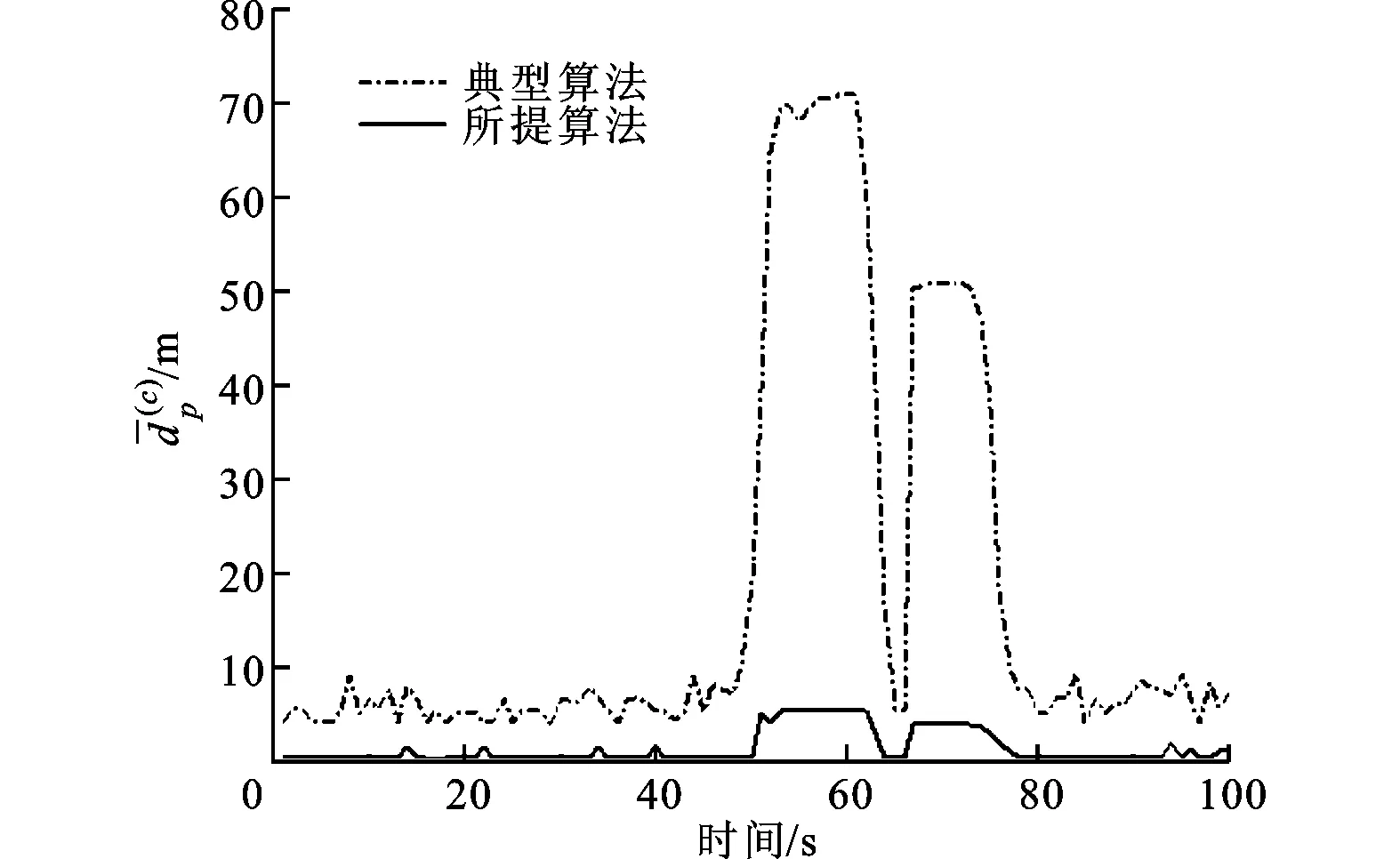
图3 50次蒙特卡罗的OSPA

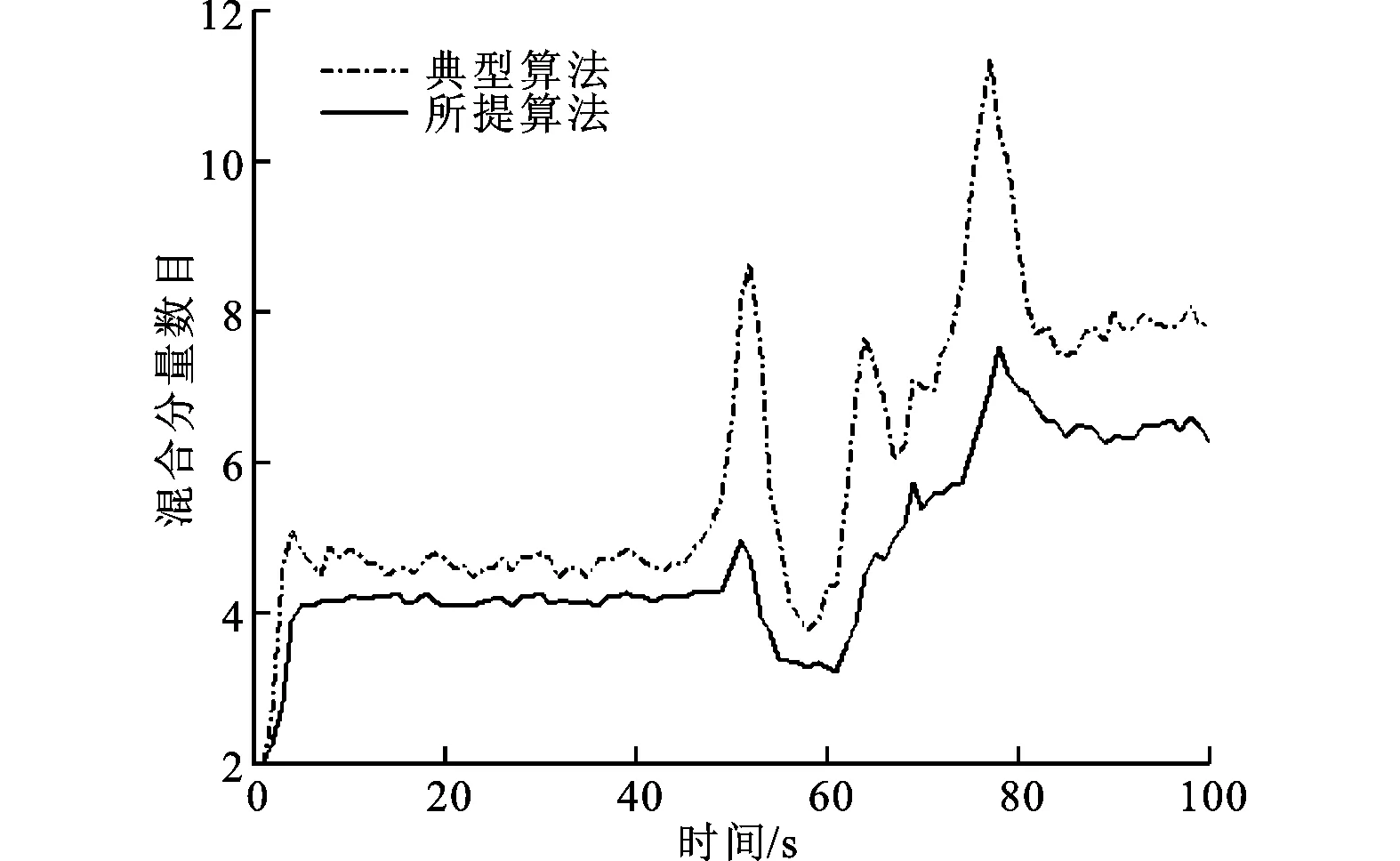
图4 两种算法的混合分量数目对比

4 结 论

针对拓展目标概率假设密度滤波器高斯混合实现中的关键量测集合分割问题,提出了基于有限混合模型的量测集合分割算法,对量测集合的所有可能分割方式进行近似。算法依据拓展目标的多量测分布在拓展目标附近的事实,把量测集合的近似分割问题归结为有限混合模型的极大似然估计问题。实验结果表明,所提基于有限混合模型的量测集合分割算法具有更好的多拓展目标跟踪性能。

[1] PULFORD G E. Taxonomy of multiple target tracking methods [J]. IET Proceeding of Radar, Sonar and Navigation, 2005, 152(2): 291-304.

[2] BLACKMAN S, POPOLI R. Design and analysis of modern tracking systems [M]. Norwood, USA: Artech House, 1999.

[3] BAR S Y, LI Xiaorong. Multitarget-multisensor tracking: principles and techniques [M]. Storrs, USA: YBS Publishing, 1995.

[4] MAHLER R. Multi-target Bayes filtering via first-order multi-target moments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[5] MAHLER R. PHD filters of higher order in target number [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.

[6] MAHLER R. Statistical multisource-multitarget information fusion [M]. Norwood, USA: Artech House, 2007.

[7] MAHLER R, VO B T, VO B N. Forward-backward probability hypothesis density smoothing [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 707-728.

[8] VO B N, VO B T, MAHLER R. Closed-form solutions to forward-backward smoothing [J]. IEEE Transactions on Signal Processing, 2012, 60(1): 2-17.

[9] 闫小喜, 韩崇昭. 应用Dirichlet分布的概率假设密度多目标跟踪 [J]. 西安交通大学学报, 2011, 45(2): 6-10.

YAN Xiaoxi, HAN Chongzhao. Multiple target tracking by probability hypothesis density based on Dirichlet distribution [J]. Journal of Xi’an Jiaotong University, 2011, 45(2): 6-10.

[10]VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multi-target filtering with random finite sets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.

[11]VO B N, MA Wing-kin. The Gaussian mixture probability hypothesis density filter [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.

[12]VO B T, VO B N, CANTONI A. Analytic implementations of the cardinalized probability hypothesis density filter [J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.

[13]GILHOLM K, SALMOND D. Spatial distribution for tracking extended objects [J]. IEEE Proceedings of Radar, Sonar and Navigation, 2005, 152(5): 364-371.

[14]VERMAAK J, IKOMA N, GODSILL S J. Sequential Monte Carlo framework for extended object tracking [J]. IEEE Proceedings of Radar, Sonar and Navigation, 2005, 152(3): 353-363.

[15]ANGELOVA D, MIHAYLOYA L. Extended object tracking using Monte Carlo methods [J]. IEEE Transactions on Signal Processing, 2008, 56(2): 825-832.

[16]KOCH J W. Bayesian approach to extended object and cluster tracing using random matrices [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.

[17]VO B T, VO B N, CANTONI A. Bayesian filtering with random finite set observations [J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1313-1326.

[18]MAHLER R. PHD filters for nonstandard targets: I extended object [C]∥The 12th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2009: 915-921.

[19]GRANSTROM K, LUNDQUIST C, ORGUNER O. Extended target tracking using a Gaussian-mixture PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.

[20]FIGUEIREDO M, JAIN A K. Unsupervised learning of finite mixture models [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2002, 24(3): 381-396.

[21]ZIVKOVIC Z, HEIJDEN F V. Recursive unsupervised learning of finite mixture models [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2004, 26(5): 651-656.

[22]HOFFMAN J, MAHLER R. Multitarget miss distance via optimal assignment [J]. IEEE Transactions on Systems, Man and Cybernetics: Part A, 2004, 34(3): 327-336.

[23]SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters [J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.

(编辑 赵炜)

APartitionAlgorithmofMeasurementSetsforExtendedObjects

YAN Xiaoxi1,HAN Chongzhao2,LI Wei2,LIAN Feng2

(1. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China;2. School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

An approximate partition algorithm of measurement sets is proposed to overcome the problem that it is impossible to implement all the possible partitions of a measurement set in density filters with extended object probability hypothesis, and the algorithm bases on a finite mixture model. The finite mixture model is used to fit the measurement set and then the partition of the measurement set is implemented. The expectation maximization algorithm is employed to obtain the maximum likelihood estimation of mixture parameters. Then, the conditional probability of the measurement source is applied in partitioning the measurement set. Simulation results show that the proposed algorithm is superior to typical partition algorithm of measurement sets in extended object tracking.

extended object tracking; probability hypothesis density; measurement set partition; finite mixture model

2014-03-08。

闫小喜(1981—),男,博士,讲师。

国家自然科学基金资助项目(61304261);江苏大学高级人才启动基金资助项目(12JDG076)。

时间:2014-07-02

10.7652/xjtuxb201409004

TP274

:A

:0253-987X(2014)09-0019-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140702.1107.002.html