自适应量子交叉克隆选择算法
戴红伟,杨玉,王永泉,李存华
(1.淮海工学院智能信息系统研究所, 222005, 江苏连云港; 2.曼彻斯特大学控制系统中心,M139PL, 英国曼彻斯特; 3.西安交通大学机械工程学院, 710049, 西安)
自适应量子交叉克隆选择算法
戴红伟1,2,杨玉1,王永泉3,李存华1
(1.淮海工学院智能信息系统研究所, 222005, 江苏连云港; 2.曼彻斯特大学控制系统中心,M139PL, 英国曼彻斯特; 3.西安交通大学机械工程学院, 710049, 西安)
为克服传统克隆选择算法易于陷入局部最优的缺点,提出了自适应量子交叉免疫算法。自适应量子交叉算子在算法演化初期通过高适配度抗体对低适配度抗体的影响,加速收敛过程,而在算法演化后期,利用低适配度抗体对高适配度抗体的扰动,增加算法跳出局部最优的概率。对旅行商问题、单目标和多目标孔群加工路径优化问题所做的计算,结果表明:自适应量子克隆选择算法能有效平衡全局搜索和局部挖掘能力,在收敛速度和稳定性上优于同类克隆选择算法和其他启发式算法。
自适应量子交叉;孔群加工路径优化;多目标优化
孔群加工作为数控加工中的典型过程,加工路径选择的合理性将直接影响加工效率和加工成本。以缩短刀具移动距离、减少刀具更换次数和刀具逆向变换次数为目标的孔群加工路径优化问题(HMPOP)成为孔群加工的关键问题。
孔群加工路径优化本质上属于组合优化问题,随着问题规模的增大,其解空间存在的“组合爆炸”现象使得传统的数学规划方法难以有效实施。文献[1-2]分别采用简单遗传算法和基于联赛选择算子与模拟退火交叉算子的改进遗传算法对HMPOP问题进行了优化。也有研究者将蚁群算法、微粒群算法和人工鱼群算法应用于HMPOP问题[3-5]。然而,上述算法都是将HMPOP简化为只考虑刀具移动成本的单目标优化问题。人工免疫系统、模拟生物免疫系统固有的自主学习、免疫记忆和分布并行处理能力等信息处理机制,为解决工程问题提供了新颖的方法和手段[6-7]。文献[8]采用人工免疫算法对HMPOP问题进行求解,该算法虽然针对刀具移动距离和刀具逆序变换次数两项指标进行多目标优化,但在单目标优化求解中其性能仍不如改进遗传算法和鱼群算法的性能,未能体现人工免疫算法在求解优化问题中的优势。
基于量子重叠与牵连原理的量子计算为有效解决复杂优化问题提供了新的思路[9]。为克服传统克隆选择算法易陷入局部最优的缺点,受电子双向跃迁物理现象的启发,本文针对多目标孔群加工路径优化问题提出了自适应量子交叉免疫算法,该算法能有效平衡全局搜索和局部挖掘能力,在收敛速度和稳定性上优于同类启发式算法。
1 量子交叉算子
受量子机制的启发,Narayanan提出了全干扰交叉算子[10],文献[11]将该算子引入克隆选择算法,较好地解决了受限多播路由问题。然而,该算子采取基于位置信息的被动选择策略,不能有效解决旅行商问题。为克服经典全干扰交叉算子的局限性,提出了自适应量子交叉算子。
1.1 释能交叉算子
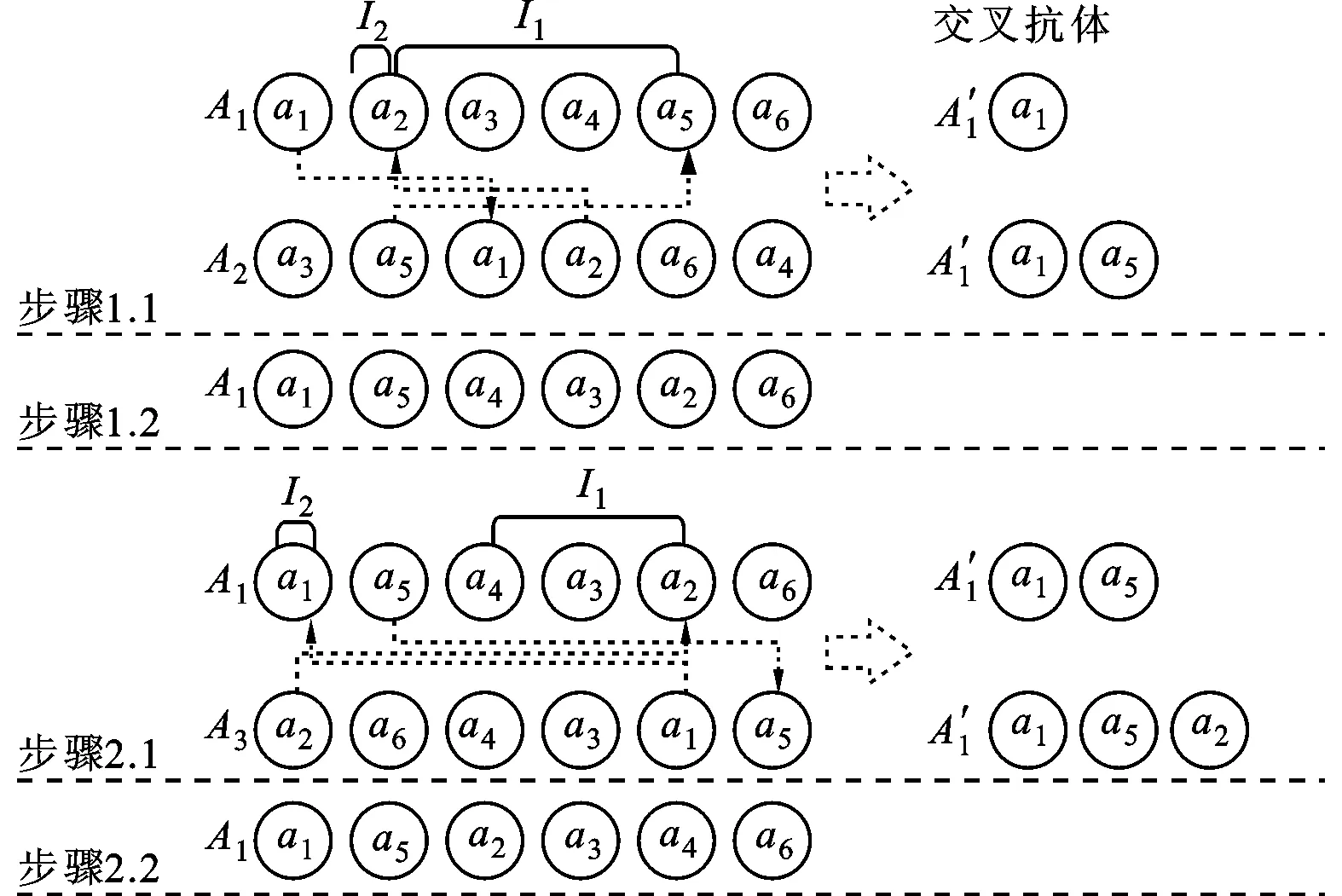
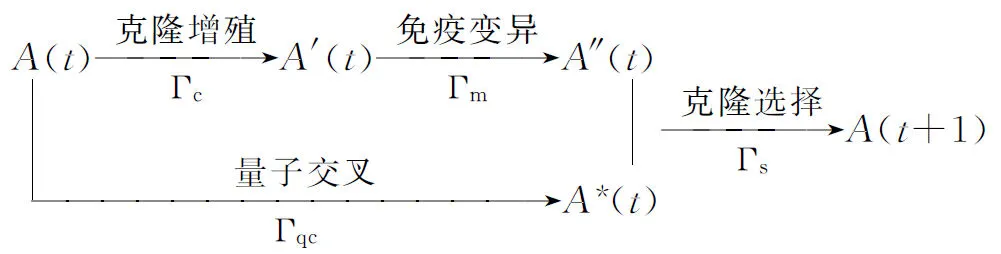
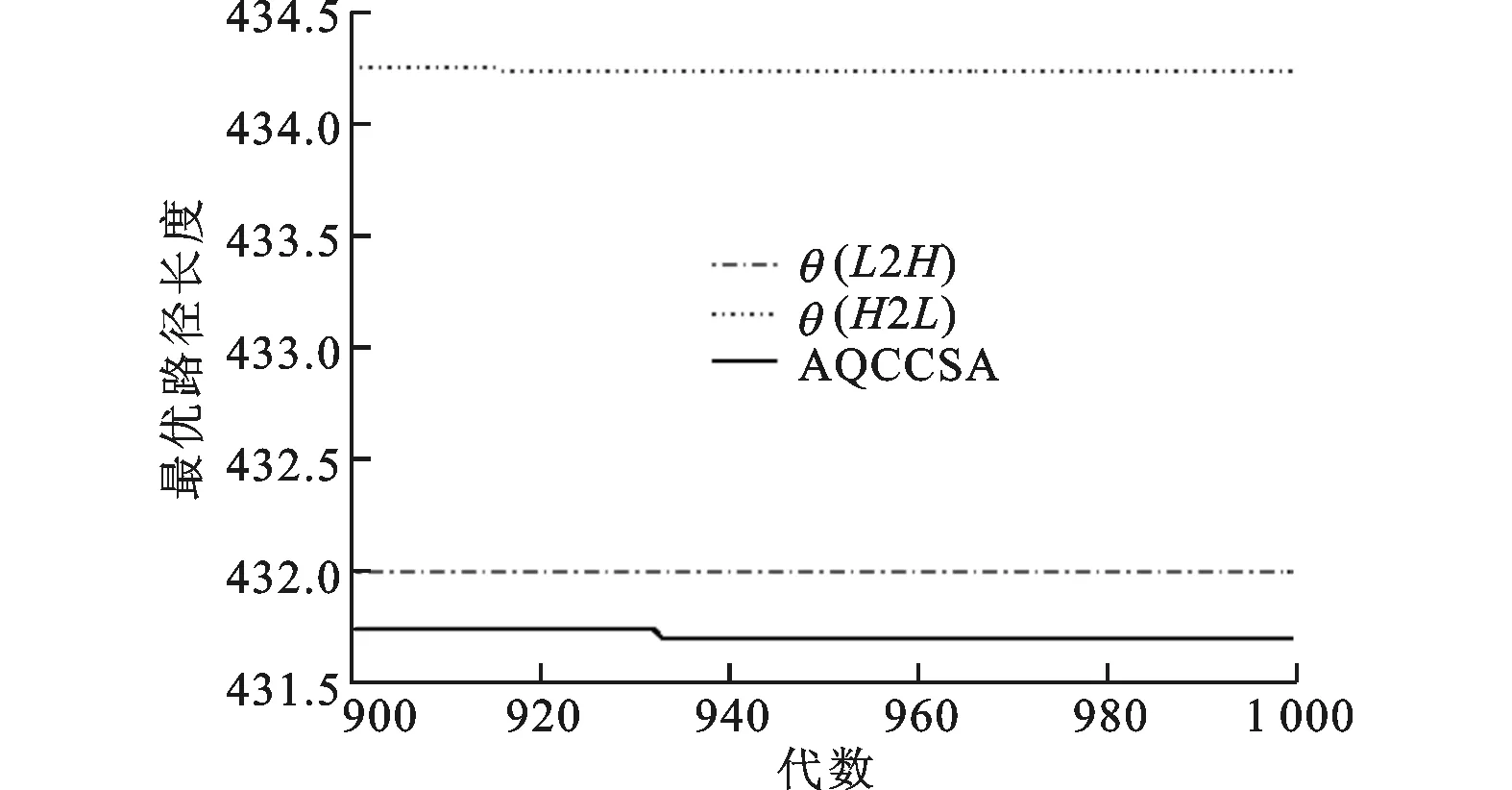
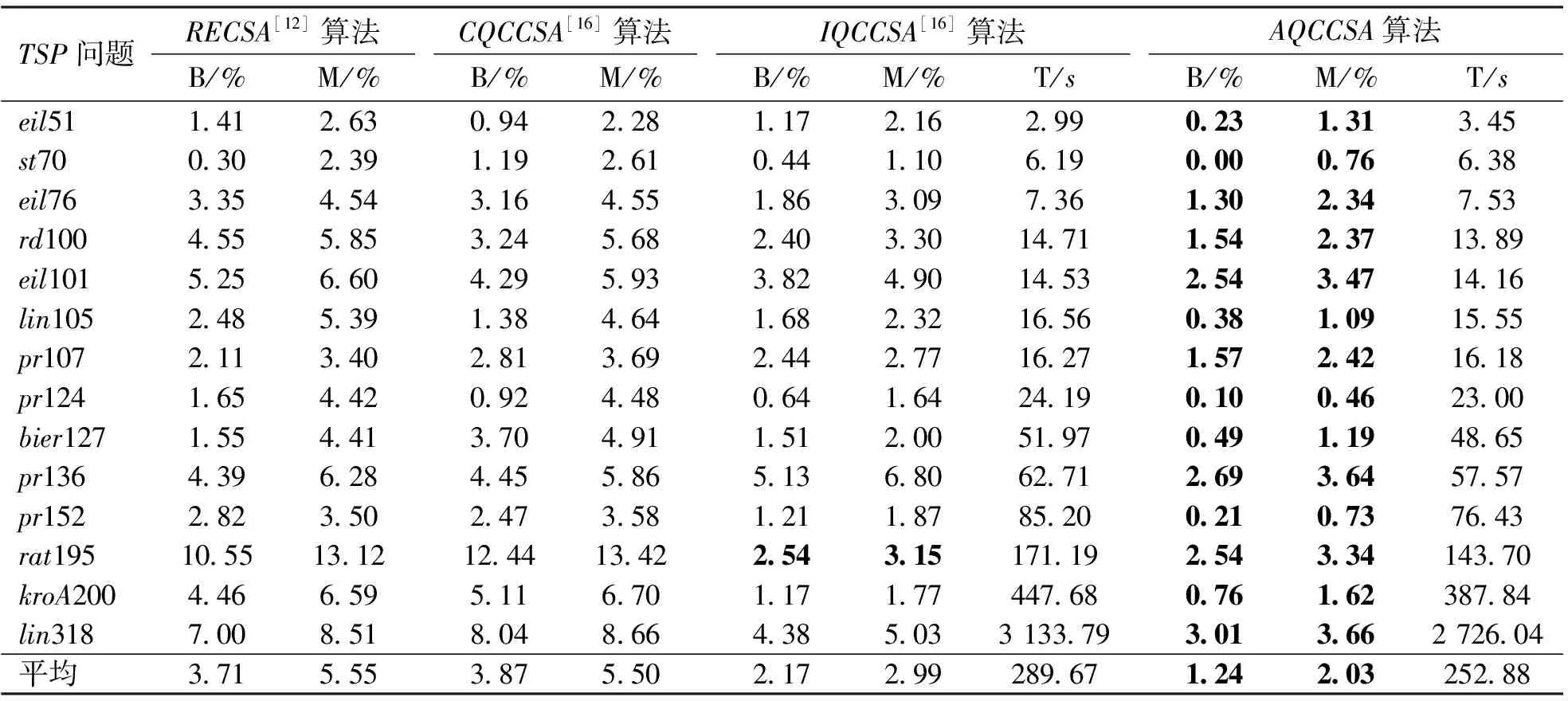
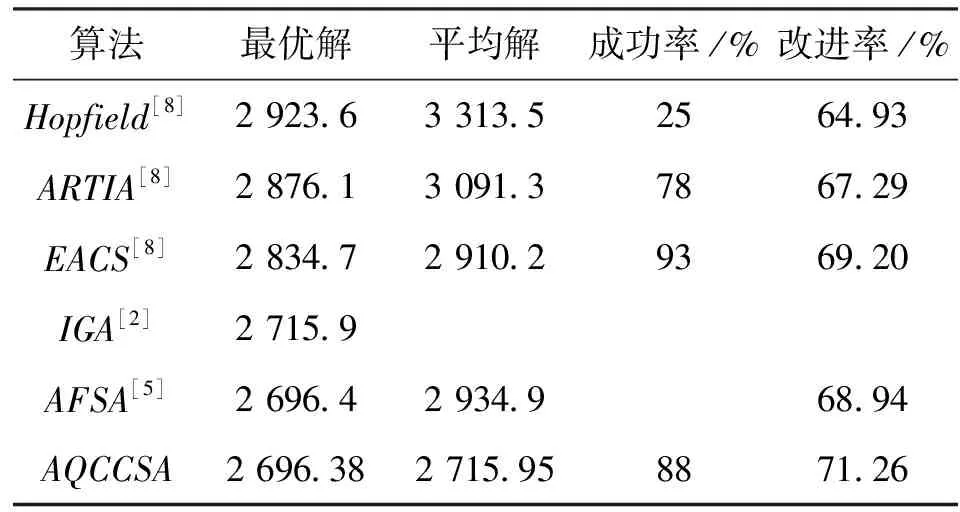
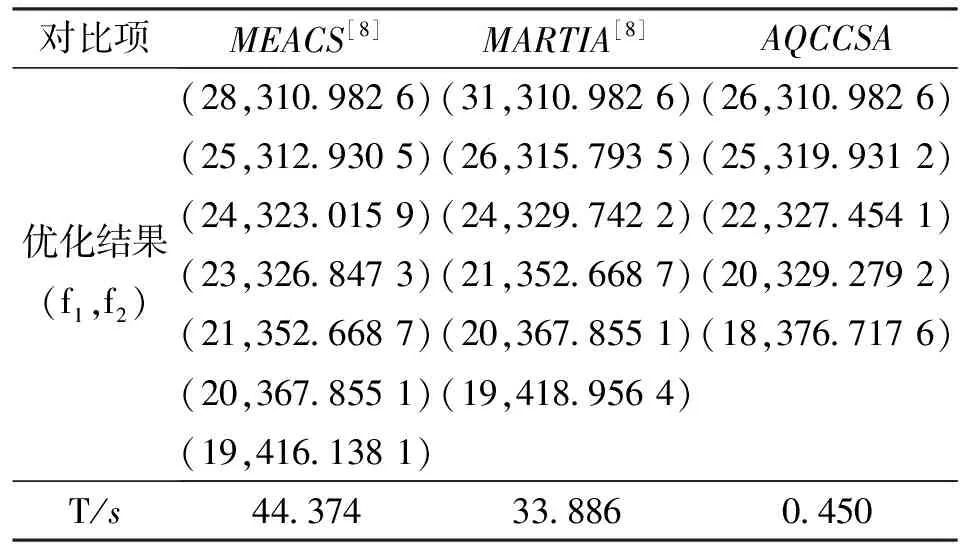
释能交叉算子θ(H2L)模拟电子通过释放能量完成从高能态到低能态的跃迁,描述了从高适配度抗体到低适配度抗体构造交叉解的过程。如图1所示,该过程为:从抗体A1中随机选取一城市,比如a1,然后跃迁至抗体A2;比较A2中与城市a1相邻的两个城市a2、a5到a1的距离,如果Dis(a5,a1) 图1 释能交叉算子θ(H2L)模拟过程示意图 1.2 吸能交叉算子 吸能交叉算子θ(L2H)模拟电子从低能轨道跃迁至高能轨道吸收能量的过程,如图2所示。不同于释能交叉算子θ(H2L),在吸能交叉算子θ(L2H)中增加了低适配度抗体对高适配度抗体的影响。 图2 吸能交叉算子θ(L2H)模拟过程示意图 步骤1.1:从A1中随机选取一城市,比如a1,跃迁至A2,确定A2中a1的左右相邻城市为a5、a2;在A1中执行反转操作I1和I2,I1为反转子片段a2-a3-a4-a5,使得a1与a5相连,I2为反转子片段a2-a2;假设反转操作I1能产生更短的巡回路径,则选择a5作为交叉抗体的当前城市。 步骤1.2:动态更新抗体A1。 步骤2.1:跃迁至抗体A3,根据a5在A3中相邻城市的信息a1、a2,在A1中执行反转操作I1和I2,即反转子片段a1-a1与子片段a4-a3-a2;如果反转操作I2能产生更短的巡回路径,则选择a2作为交叉抗体的当前城市。 步骤2.2:动态更新抗体A1。 依次类推,直到构成一个可行解。 1.3 自适应量子交叉算子 对比释能交叉算子θ(H2L)与吸能交叉算子θ(L2H)可以发现:θ(H2L)体现了高适配度抗体对低适配度抗体的影响,促使算法可以更快速地向优质解聚集,提高收敛速度;θ(L2H)体现了低适配度抗体对高适配度抗体的影响,虽然从低适配度抗体获取的信息有可能会破坏高适配度抗体的优质模式,但是这种扰动却可以提高算法跳出局部最优的概率。自适应量子交叉算子AQC的伪代码描述如下 fort=0:T QJP=(T-t)/T if rand( ) θ(H2L) else θ(L2H) end if end for 式中:QJP为量子跃迁概率控制因子;T为总代数,t为当前代数;rand()为随机函数。 2.1 自适应量子交叉克隆选择算法 克隆选择算法是基于克隆选择学说而形成的一种免疫计算方法,其主要过程包括克隆增殖、免疫变异和免疫选择3个环节[11],量子交叉克隆选择算法可表示为如下的免疫进化过程 假设种群规模为N,即A={A1,A2,…,AN},其中Ai(i=1,2,…,N)为适配度从高到低排列的N个抗体,则免疫进化的主要步骤可描述如下。 (1)克隆增殖Γc:对抗体Ai进行规模为pi的克隆增殖,假设M为克隆增益因子,则pi可表示为 (1) 经过克隆增殖之后,种群变为 (2) (2)免疫变异Γm:针对克隆后的种群进行超变异和受体编辑操作[12],免疫变异不影响种群规模,变异后的种群为 (3) (4) (4)克隆选择Γs:依据适配度从当前种群中挑选N个优质抗体产生下一代种群A(t+1)。 重复以上过程,直到满足终止的条件,输出最终结果。 2.2 算法的收敛性分析 本文采用随机过程中的鞅理论方法对算法的收敛性进行分析。首先给出鞅列与下鞅的定义[13]。 定义1(鞅列) 如果对∀n,E(|Yn|)<∞,且对∀m有 (5) 则随机序列Yn为鞅列。如果Xn为(Yn)可知的,且对∀n,E(|Xn|)<∞,∀m有 (6) 则称Xn为(Yn)鞅列。由条件期望的性质可知,如果Xn是(Yn)鞅列,则Xn也是鞅列。 定义2(下鞅) 将式(5)、(6)中的“=” 改为“≥”,则对应的随机序列称为下鞅列。 利用鞅的性质,文献[13]已经证明了遗传算法的收敛性。其证明思路为:将算法的收敛性问题中的序列转化为某一个下鞅列或鞅序列,然后证明该序列满足鞅收敛定理的条件,获得鞅序列的收敛性,再转化为原来序列的收敛性。 基于2.1节算法实现过程的描述,克隆选择算法的目的在于生成一列种群(解){A(t),t≥0},且该列种群包含有概率分布倾向于具有最佳适配度函数的候选解。若以种群的平均适配度作为指导原则,则当且仅当种群中每个抗体适配度达到全局最大时种群的平均适配度达到最大,因此可以利用平均适配度函数的收敛性来研究克隆选择算法的收敛性。同时,每次迭代后,如果新种群的平均适配度关于当前种群的条件期望不低于当前种群的平均适配度,就可以把平均适配度函数fav(A(t))转化为一个下鞅来考察算法的收敛性,即算法保证通过各种免疫算子的作用使得下一代种群的平均适配度不低于当前种群的平均适配度。 自适应克隆选择算法中克隆增殖算子Γc完全复制父代抗体,免疫变异算子Γm在保留父代抗体信息的基础上进行小概率免疫变异,量子交叉算子Γqc在综合父代优质抗体信息的基础上产生更优质抗体,而克隆选择算子Γs确保用高适配度抗体更新父代低适配度抗体,因此自适应克隆选择算法(AQCCSA)可以保证子代种群的平均适配度不低于父代种群的平均适配度,即fav(A(t+1))≥fav(A(t))。 定理1[14]假设时刻t算法得到的种群序列为{A(t),t≥0},Φt=Φ(A(1),A(2),…,A(t))为A(1),A(2),…,A(t)可测的最小σ代数,则fav(A(t))关于Φt为下鞅,即 (7) 在定理1的条件下,设B*为全局最优解,f*为最优适应度,当种群状态有限时,有如下结论 由以上结论知,在满足定理1的条件时,自适应克隆选择算法所产生的种群的适应度必趋于最优值,算法将以概率1确保在有限迭代次数内达到问题的最优解,算法必然收敛。 2.3 算法复杂度分析 O(MNa)+O(NqcNa)= 2.4 旅行商问题 TSP是典型的NP难问题,可简单描述为:给定N个城市坐标,找出一条经过所有城市一次且仅一次的距离最短的最优路径。 本文提出的自适应交叉算子本质上是由θ(H2L)和θ(L2H)组成的混合算子,但是两种算子特性各异且具有互补性。为比较各个交叉算子的性能,本文进行了对比实验,表1给出了5个TSP问题的仿真结果,所有结果均为50次独立运行结果的平均值。从运算结果可以看出,自适应量子交叉算子(AQC)性能优于单独的θ(H2L)或θ(L2H)交叉算子。 表1 不同量子交叉算子的性能比较 注:W表示最差解对于最优解偏差的百分比;M表示平均解对于最优解偏差的百分比;B表示最好解对于最优解偏差的百分比。 为进一步分析自适应交叉算子的性能,本文采用了文献[12]所使用的群体多样性Dpop的定义 Dpop=Dsum/(N-1) (8) 式中:Dsum为群体内抗体与最优抗体差异度的和,即 (9) 其中X(Ao,Aj)表示抗体Ao、Aj包含相同边的数量。 作为群体算法,能否维持良好的群体多样性是反映算法性能的重要指标之一。根据文献[15],理想的群体多样性为前高后低,即在进化前期,较高的多样性有利于算法在更广的范围展开搜索,而在搜索的后期,较低的多样性有利于在局部空间进行开发,增加了找到全局最优解的可能性。 图3a、3b分别给出求解eil51问题的群体多样性变化和算法收敛过程(50次独立运行平均结果),图3c为最后100代的收敛过程。 (a)群体多样性变化趋势 (b)迭代收敛过程 (c)最后100代收敛过程 从图3中可以看出,几种交叉算子的群体多样性都随着迭代的进行而逐渐减小,然而自适应交叉算子却有着不同于其他交叉算子的平台期,即在某个特定时期内,群体多样性维持较为稳定的高位水平,使得算法有机会在更大的范围内进行搜索,而不至于过早陷入局部最优。针对其他TSP问题的计算结果也验证了平台期的存在及其对算法性能的有效提升。 表2给出了不同免疫算法求解TSP问题的对比结果,其中RECSA为融合受体编辑的经典克隆选择算法[12],CQCCSA、IQCCSA分别为基于经典量子干扰交叉算子和基于距离比较的量子交叉克隆选择算法[16]。城市数目在51~124之间的问题迭代1 000次,城市数目在127~195之间的问题迭代2000次,kroA200问题迭代5000次,lin318问题迭代10000次。黑体数据为几种算法中的最优值。由仿真结果可得,自适应量子交叉克隆选择算法在几乎所有TSP问题中性能优于其他算法。 为验证算法性能,本节针对机械加工中的孔群路径优化问题(HMPOP)进行求解,并与已有算法进行比较。 3.1 单目标HMPOP问题 HMPOP问题的目标就是选择合理的加工顺序,使总加工成本最小。为保证与其他算法比较的公平性,本文采用最小化刀具行进成本为优化目标,抽象为一个典型的TSP问题。优化对象为一注塑模上模,具体尺寸见文献[1]。 表2 不同算法求解TSP问题计算结果对比 注:T为运行时间。 表3为不同算法求解单目标HMPOP问题的结果对比,其中Hopfield、ARTIA(人工免疫算法)、EACS(蚁群算法)数据来自文献[8],IGA为改进遗传算法[2],AFSA为人工鱼群算法[5],AQCCSA为本文所提算法。虽然人工鱼群算法能找到已知最优解,但平均解的质量远不如本算法的质量。 表3 不同算法求解结果对比 3.2 多目标HMPOP问题 k∈{2,3,…,n-1},j∈{1,2,…,l} 则问题的目标函数为 (10) 刀具的行进成本可以表示为 (11) 同时,要求逆序变向次数和刀具行进距离均为最小,该问题为多目标优化问题。 为解决多目标优化问题,本文采用快速双目标非支配排序算法[17],表4给出了不同方法求解上述多目标孔群加工路径优化问题的计算结果,其中种群规模为100,克隆增益因子为1,进化代数为3。从对比结果可以看出,AQCCSA解的质量明显好于另外两种算法。 表4 多目标孔群加工路径优化结果对比 为克服传统克隆选择算法易于陷入局部最优的缺点,本文针对多目标孔群加工路径优化问题提出自适应量子交叉免疫算法。自适应交叉算子模拟了物理学中电子双向跃迁的现象,即电子既可以从高能轨道通过释放能量跃迁至低能轨道,也可以通过吸收能量从低能轨道跃迁至高能轨道。该算子在算法演化初期通过高适配抗体对低适配抗体的影响,加速收敛过程,而在算法演化后期,利用低适配度抗体对高适配度抗体的扰动,增加算法跳出局部最优的概率。不同于其他交叉算子,自适应交叉算子在某个特定时期内存在平台期的现象,使群体多样性维持较稳定的高位水平,算法有更多的机会在更大的范围内进行搜索,而不至于过早陷入局部最优。该算法能有效平衡全局搜索和局部挖掘能力,在收敛速度和稳定性上优于同类启发式算法。 [1] 周正武, 丁同梅. 基于TSP和GA孔群加工路径优化问题的研究 [J]. 组合机床与自动化加工技术, 2007(7): 30-32. ZHOU Zhengwu, DING Tongmei. Research on holes machining path planning optimization with TSP and GA [J]. Modular Machine Tool & Automatic Manufacturing Technique, 2007(7): 30-32. [2] 凌玲, 胡于进, 王青青, 等. 基于改进遗传算法的孔群加工路径优化 [J]. 华中科技大学学报, 2009, 37(8): 88-91. LING Ling, HU Yujin, WANG Qingqing, et al. Holes machining path optimization using the improved genetic algorithm [J]. Journal of Huazhong University of Science and Technology, 2009, 37(8): 88-91. [3] ABBAS A, ALY M, HAMZA K. Optimum drilling path planning for a rectangular matrix of holes using ant colony optimisation [J]. International Journal of Production Research, 2011, 49(19): 5877-5891. [4] ZHU Guangyu, ZHANG Weibo. Drilling path optimization by the particle swarm optimization algorithm with global convergence characteristics [J]. International Journal of Production Research, 2008, 46(8): 2299-2311. [5] 蔡云, 周立炜. 人工鱼群算法在孔群加工路径优化中的应用研究 [J]. 武汉科技大学学报, 2011, 34(3): 182-185. CAI Yun, ZHOU Liwei. Holes machining path optimization using an artificial fish swarm algorithm [J]. Journal of Wuhan University of Science and Technology, 2011, 34(3): 182-185. [6] 焦李成, 杜海峰, 刘芳, 等. 免疫优化:计算、学习与识别 [M]. 北京: 科学出版社, 2006. [7] JIAO Licheng, LI Yangyang, GONG Maoguo, et al. Quantum-inspired immune clonal algorithm for global optimization [J]. IEEE Transactions on System, Man and Cybernetics: Part B, 2008, 38(5): 1234-1253. [8] 肖人彬, 陶振武. 孔群加工路径规划问题的进化求解 [J]. 计算机集成制造系统, 2005, 11(5): 682-689. XIAO Renbin, TAO Zhenwu. Solution to holes machining path planning by evolutionary methods [J]. Computer Integrated Manufacturing System, 2005, 11(5): 682-689. [9] LI Yangyang, XIANG Rongrong, JIAO Licheng, et al. An improved cooperative quantum-behaved particle swarm optimization [J]. Soft Computing, 2012, 16(6): 1061-1069. [10]NARAYANAN A, MOORE M. Quantum-inspired genetic algorithm [C]∥Proceedings of IEEE International Conference on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1996: 61-66. [11]李阳阳, 焦李成. 量子克隆多播路由算法 [J]. 软件学报, 2007, 18(9): 2063-2069. LI Yangyang, JIAO Licheng. Quantum clonal algorithm for multicast routing problem [J]. Journal of Software, 2007, 18(9): 2063-2069. [12]GAO Shangce, DAI Hongwei, YANG Gang, et al. A novel clonal selection algorithm and its application to traveling salesman problems [J]. IEICE Transaction on Fundamentals of Electronics, Communications and Computer Sciences, 2007, 90(10): 2318-2325. [13]徐宗本, 张讲社, 郑亚林. 计算智能中的仿生学: 理论与算法 [M]. 北京: 科学出版社, 2003. [14]洪露, 纪志成, 龚成龙. 一种改进型克隆选择算法及其几乎处处强收敛性研究 [J]. 控制与决策, 2010, 25(5): 725-729. HONG Lu, JI Zhicheng, GONG Chenglong. On an improved clonal selection algorithm and its almost sure strong convergence [J]. Control and Decision, 2010, 25(5): 725-729. [15]CHANG Pei-Chann, HUANG Wei-Hsiu, TING Ching-Jung. Dynamic diversity control in genetic algorithm for mining unsearched solution space in TSP problems [J]. Expert Systems with Applications, 2010, 37(4): 1863-1878. [16]DAI Hongwei, YANG Yu, LI Cunhua, et al. Quantum interference crossover-based clonal selection algorithm and its application to traveling salesman problem [J]. IEICE Transaction on Information & System, 2009, 92(1): 78-85. [17]刘敏, 曾文华, 赵建峰. 一种快速的双目标非支配排序算法 [J]. 模式识别与人工智能, 2011, 24(4): 538-547. LIU Min, ZENG Wenhua, ZHAO Jianfeng. A fast biobjective non-dominated sorting algorithm [J]. Pattren Recognition and Artificial Intelligence, 2011, 24(4): 538-547. [本刊相关文献链接] 任茂栋,梁晋,唐正宗,等.数字图像相关法中的优化插值滤波器.2014,48(7):65-70.[doi:10.7652/xjtuxb201407012] 靳峰,冯大政.利用空间序列描述子的快速准确的图像配准算法.2014,48(6):19-24.[doi:10.7652/xjtuxb201406004] 吴仁斌,姚敏立,贾维敏,等.采用幅度响应约束的鲁棒自适应波束形成算法.2014,48(4):109-114.[doi:10.7652/xjtuxb201404019] 李彬,宋立明,李军,等.长叶片透平级多学科多目标优化设计.2014,48(1):1-6.[doi:10.7652/xjtuxb201401001] 郝红侠,刘芳,焦李成,等.采用结构自适应窗的非局部均值图像去噪算法.2013,47(12):71-76.[doi:10.7652/xjtuxb 201312013] 李帝辰,席光,孙中国.无网格粒子法中复杂二维形状的均布离散方法.2013,47(11):120-126.[doi:10.7652/xjtuxb201311021] 刘光辉,任庆昌,孟月波,等.自适应先验马尔可夫随机场模型的图像分割算法.2013,47(10):62-67.[doi:10.7652/xjtuxb201310011] 侯兴松,张兰,肖琳.合成孔径雷达图像的贝叶斯压缩感知重构算法.2013,47(8):74-79.[doi:10.7652/xjtuxb201308013] (编辑 赵炜) AdaptivveQuantumCrossoverClonalSelectionAlgorithm DAI Hongwei1,2,YANG Yu1,WANG Yongquan3,LI Cunhua1 (1. Institute of Intelligent Information System, Huaihai Institute of Technology, Lianyungang, Jiangsu 222005, China;2. Control System Centre, University of Manchester, Manchester M139PL, UK; 3. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China) A clonal selection algorithm with adaptive quantum crossover (AQCCSA) is proposed to overcome the premature convergence drawback of traditional clonal selection algorithms (CSA) and to solve the holes machining path optimization problems (HMPOP). The effect of high affinity antibodies on low affinity antibodies is used to accelerate the convergence process in the first half evolution process. Then the disturbance effect of low affinity antibodies on high affinity antibodies is used to help the algorithm escaping from local optimum in the last half evolution process. Experimental results on traveling salesman problems (TSP), single-objective and multi-objective HMPOP show that the proposed algorithm achieves a good balance between global searches and local mining, and the convergence speed and robustness of the algorithm are better than those of other CSAs and heuristic algorithms. adaptive quantum crossover; holes machining path planning;multi-objective optimization 2014-03-19。 戴红伟(1975—),男,副教授。 国家自然科学基金资助项目(61203325,51375367);江苏省自然科学基金资助项目(BK2012663)。 时间:2014-07-03 10.7652/xjtuxb201409002 TP399;TP301.6 :A :0253-987X(2014)09-0006-07 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140703.1130.003.html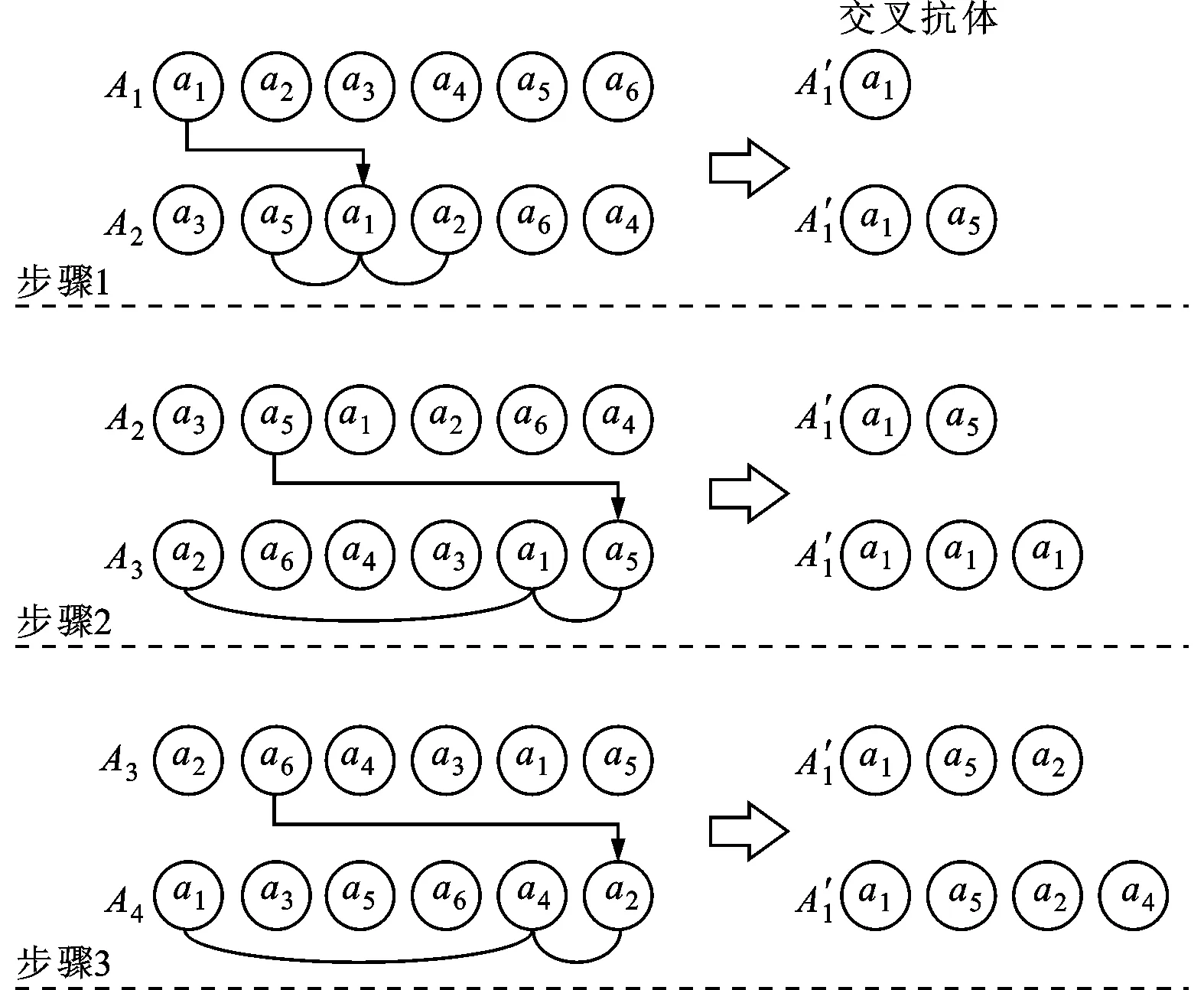
2 量子交叉免疫克隆算法及其验证
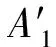
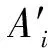
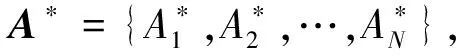

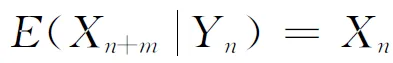
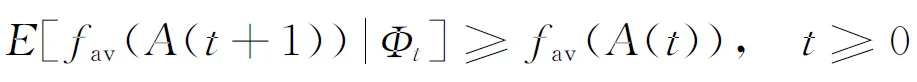
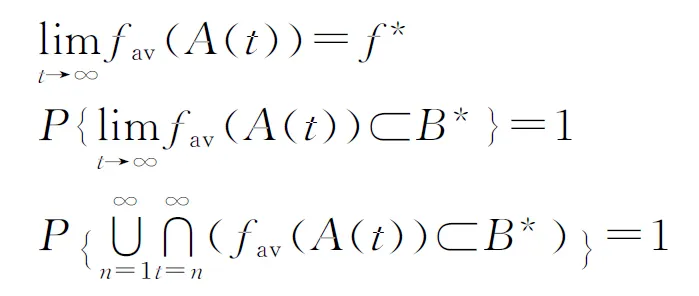
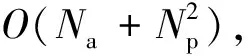
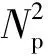



3 孔群加工路径优化问题


4 结 论

