单级压力调节阀的阻尼孔射流响应特性分析

闵为,冀宏,王峥嵘,王金林

(1.兰州理工大学能源与动力工程学院,730050,兰州; 2.甘肃省液压气动工程技术研究中心,730050,兰州)

单级压力调节阀的阻尼孔射流响应特性分析

闵为1,2,冀宏1,2,王峥嵘1,2,王金林1,2

(1.兰州理工大学能源与动力工程学院,730050,兰州; 2.甘肃省液压气动工程技术研究中心,730050,兰州)

为揭示带阻尼孔的压力调节阀的稳定性机理,运用流固耦合方法计算了阶跃和周期性流量脉动信号激励下阀芯的响应过程,得出了不同阀腔结构条件下阀芯的轴向振动特征和阀口前端阀芯表面压力分布及其变化规律。研究发现,阀内阻尼孔射流流束冲击阀芯表面,使得阀口前端阀芯表面呈现射流冲击区和静压区两部分,阀芯的轴向振动幅值主要取决于射流冲击区和静压区二者液压力的相位差,当静压区和射流冲击区的液压力相位差趋于180°时,阀芯及其轴向振动幅值将大幅减小。研究结果为压力调节阀的设计提供了新思路。

压力调节阀;阻尼孔射流;流固耦合;轴向振动;稳定性机理

压力调节阀是各种液压系统中不可缺少的元件之一,工作时阀口开度小、阀口前后压差大,油液流经阀口时处于高速喷流状态。多级压力调节阀的导阀(单级压力调节阀)阻尼系数较小,在液压泵或其他元件产生的流量变化及脉动的影响下,极易引起阀芯甚至是整个压力调节阀处于不稳定状态[1]。因此,研究带阻尼孔的单级压力调节阀(导阀)在扰动射流作用下的响应特性,对于研究压力调节阀的稳定性具有重要意义。

关于压力调节阀的静、动态特性和稳定性,许多研究人员开展了细致的研究工作。Oshima通过半剖模型对不同结构的锥阀进行了实验研究[2],但主要是针对固定开口条件下的稳态流场;文献[3-4]采用数学建模的方法对压力调节阀的静、动态特性和稳定性进行了研究;Tsukiji采用流场仿真的方法研究了影响阀芯轴向运动的关键因素[5];Erhard通过仿真分析了不同结构压力调节阀的性能差异[6];文献[7]指出:Green的实验研究表明,阀口流动从层流到湍流的过渡过程、压力调节阀与液压系统中其他元件的耦合动作、系统供油压力的波动,都会导致阀芯出现轴向振动和不稳定现象;Waldling研究了出口管路对阀芯稳定性的影响,结果表明,弹簧动力学特性和出口管路长度对阀芯稳定性的影响远大于阀腔容积的影响[8];Kasai研究了进、出口管路对阀芯稳定性的影响,指出外部周期性扰动是导致锥阀出现不稳定现象的主要原因[9-10]。

上述仿真和实验研究都是从结构参数或实验现象的角度来阐述影响压力调节阀的调节特性和稳定性的因素,并未从理论上揭示影响压力调节阀静、动态特性和轴向振动的机理。

本文针对作为导阀使用的带阻尼孔的单级压力调节阀,运用流固耦合方法描述了不同阀腔结构的阀芯轴向动态运动过程,得出了阶跃和周期性流量脉动信号作用下阀芯位移及阀口前腔流场参数的瞬态变化特征,分析了瞬态流场下阀口前腔阀芯表面压力分布及变化特征对压力调节阀阀芯轴向运动特性的影响,揭示了影响压力调节阀静、动态特性和稳定性的主要因素。该研究结果为压力调节阀的设计提供了新思路。

1 计算模型及条件

本文采用comsol多场耦合软件对压力调节阀阀芯-流场进行了多场耦合建模。通过调用微机电模块中的流固耦合计算模式,运用ale移动网格,以阀芯为固体域、阀芯前后流场为流体域,对阀芯的轴向运动过程进行了直接流固耦合计算。其中,弹簧力以集中载荷的形式施加于阀芯尾部,阀芯表面所受流场的作用力通过流场中的压力对阀芯表面积分求得。阀芯在轴向可自由运动,其力平衡方程如下

(1)

式中:A为阀芯表面积;z为阀芯位移(由流固耦合计算得出);z0为弹簧预压缩量。

不同阀腔结构的压力调节阀计算模型(a、b、c)如图1所示。为减小计算量,将模型简化为二维轴对称结构且忽略阻尼孔前端容积,外界的一切扰动因素归结为压力调节阀的进口流量脉动。

图1中1点～4点分别表示阻尼孔进口中心点、阀口前腔中心点、阀芯前端平面中心点、阀芯前端平面边缘点,L1为射流冲击长度(阻尼孔出口至阀芯前端面的距离),D2、L2分别为模型b中增加阀腔体积时对应的阀腔直径和相关长度。

(a)常用阀腔(模型a)

(b)增加阀腔直径(模型b)

(c)增加阀腔长度(模型c)

模型的主要结构参数为:阀座直径d1=4 mm;阻尼孔直径d2=1.2 mm;阻尼孔长度l=10mm;阀芯前端面直径d3=2.2 mm;阀芯质量m=3.5 g;调压弹簧刚度k=60N/mm;阀芯半锥角α1=10°;阀座半锥角α2=60°。锥阀阀口前腔结构参数如表1所示。

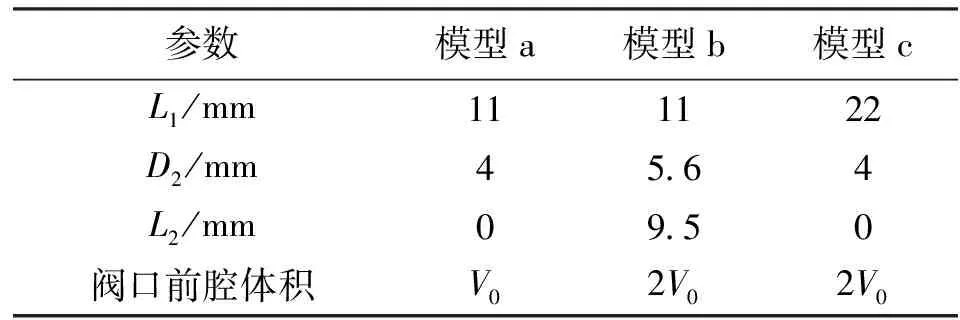
表1 锥阀阀口前腔结构参数

不考虑温度变化对黏度和密度影响时的流场参数为:油液动力黏度μ=0.04 Pa·s。流场控制方程采用弱可压缩性纳维-斯托克斯方程,其中密度为压力的函数,即

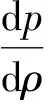
(2)

式中:K为弹性模量,取1.1 GPa;p为流场压力;ρ为油液密度。

对式(2)积分得

ρ=e(p+C)/K

(3)

将初始条件p=101 kPa、ρ=900kg/m3代入式(3),可求得积分常数C=7.48×109。

计算边界条件为:阻尼孔的前端面为进口边界,流量为输入值;阀芯后端的流场边界为出口边界,压力为恒定值101 kPa;阀腔内壁为固定无滑移边界;阀芯表面为移动壁面,速度为固体域的流固耦合运动速度;流体域和固体域的对称轴为轴对称边界。计算初始条件为:流场初始压力为101 kPa;弹簧预压缩量z0=3 mm;初始阀口开度为0.1 mm。

采用上述参数和条件,可保证阀芯前后流场的连续性。

2 计算结果及分析

2.1 阶跃激励信号

为准确反映压力调节阀的静、动态特性,在模拟压力调节阀突变输入信号下的瞬态调节过程中,首先模拟进口边界输入流量q=1.41 L/min时的流固耦合过程,当流场作用力与弹簧力达到平衡状态,且在t=4 ms输入流量q=1.93 L/min时,阀芯从一个平衡状态跃迁到另一个平衡状态,阶跃响应过程如图2所示。

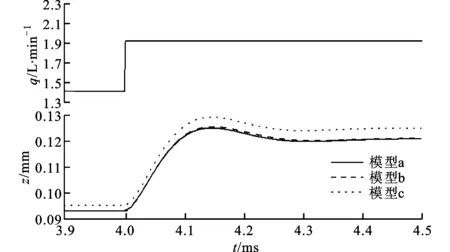
图2 不同阀腔结构下锥阀的阶跃响应曲线

从图2中看出:当输入流量q=1.41 L/min时,模型a、b的阀芯位移均为0.094 mm,模型c的阀芯位移为0.095 5 mm;当输入流量q=1.93 L/min时,模型a、b的阀芯位移均为0.12 mm,模型c的阀芯位移为0.125 mm;在阶跃响应过程中,模型a的超调量为4.3%,模型b的超调量为4.7%,模型c的超调量为3.4%,调节时间均为0.4 ms。可见,模型a、b的静、动态特性基本一致,而模型c在阀芯位移增大时超调量减小。

阀芯运动达到稳定状态(t=5 ms、q=1.93 L/min)时,阀口前端阀芯表面的压力随阀芯半径r的变化如图3所示。由于液压油的部分动能转换为压力势能,使得阀芯表面正对阻尼孔的区域压力升高;由于阀芯锥面部分的通流面积减小,使得液压油动能增加,根据伯努利方程可知,阀芯锥面部分压力逐渐降低。从图3中看出,在r>0.6 mm的区域(除阻尼孔正对阀芯表面以外的区域),模型c的阀芯表面压力均大于模型a、b。

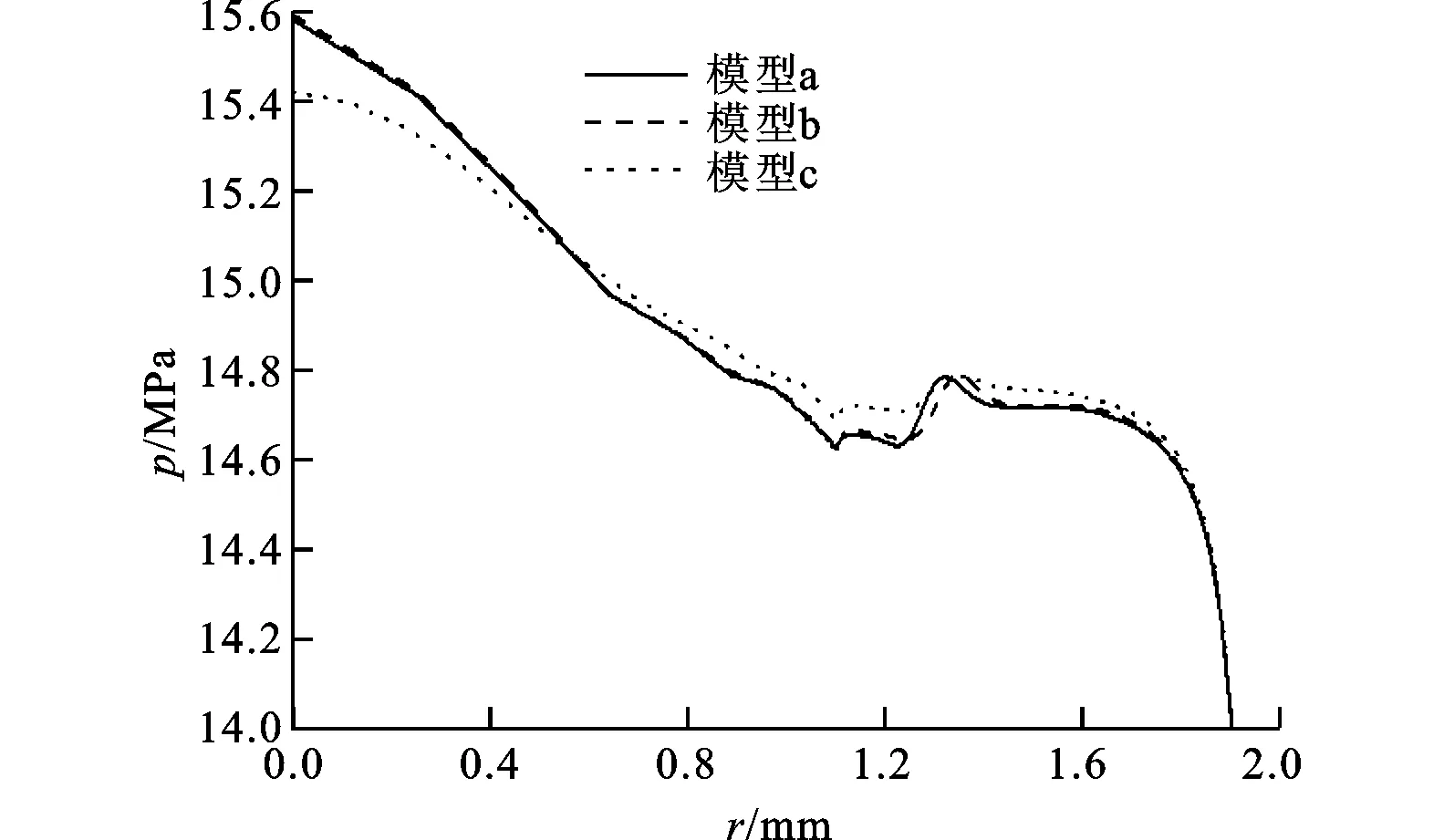
图3 t=5 ms时阀口前端阀芯表面的压力随阀芯半径的变化

2.2 周期激励信号

仅从锥阀的角度来看,浸没在液压油中的阀芯(弹簧振动系统)必然是稳定和收敛的。事实上,压力调节阀在液压泵或系统中其他元件的影响下极易发生轴向高频振荡,产生尖锐的啸叫声。为模拟压力调节阀在流量脉动作用下的瞬态工作过程,对进口边界输入周期性流量脉动信号时的流固耦合过程进行了计算。

假设提供油源的是齿数为12、转速为1 500r/min的外啮合齿轮泵,其流量脉动率为18%,为便于分析,将流量脉动信号简化为标准的正弦周期信号q=1.41+0.13sin(ωt),由此计算了时间t为0～8 ms时阀芯在流量脉动作用下的动态响应过程。

2.2.1 阀口前端阀芯表面的压力分布与相位特性模型a在定周期流量脉动信号下的阀芯位移和流场特征参数曲线如图4所示。从图4中看出,阀芯位移和各特征参数曲线均为定周期的正弦曲线,但各曲线之间存在明显的相位差。

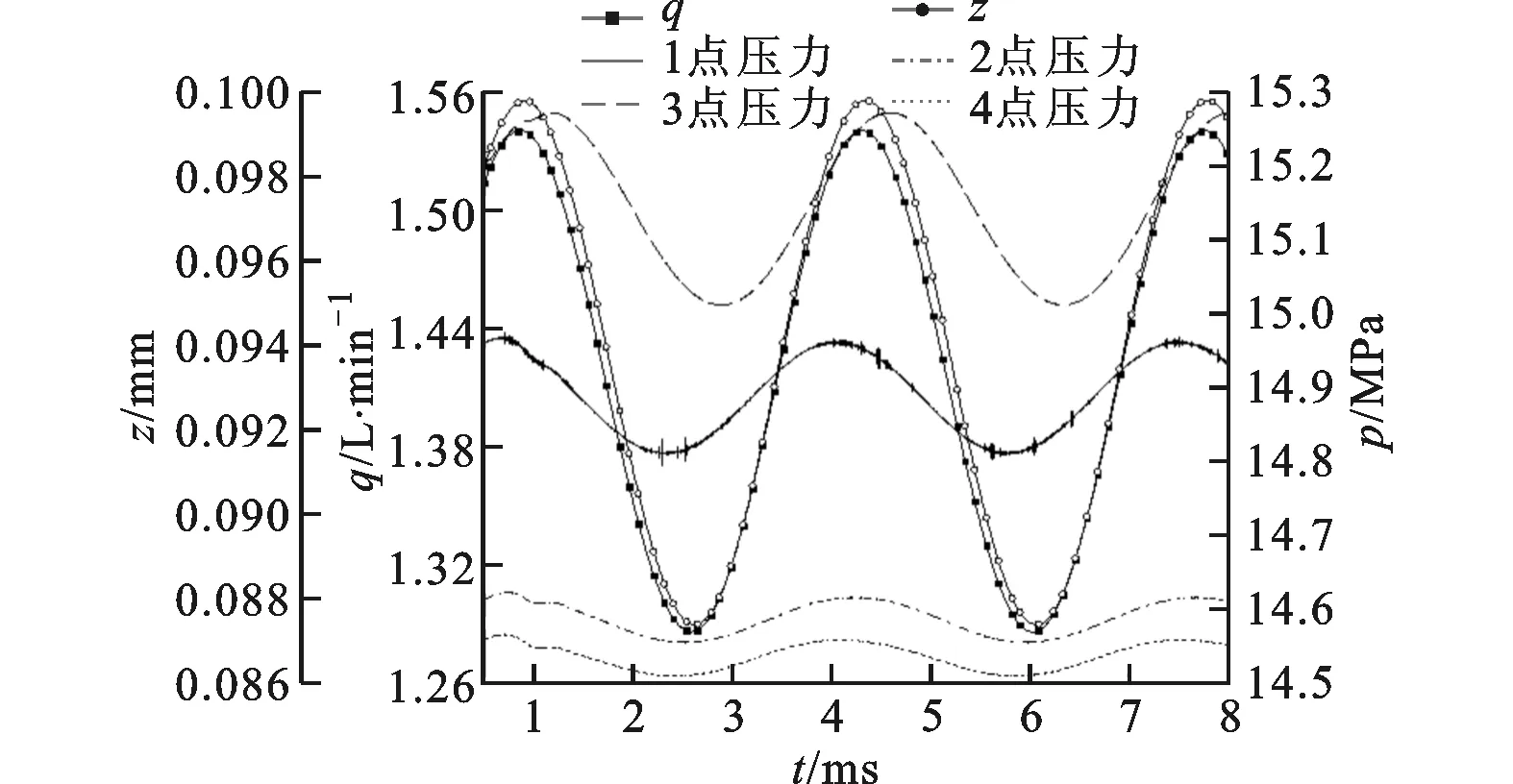
图4 模型a在定周期流量脉动信号下的阀芯位移和流场特征参数曲线

由于流固耦合计算过程中瞬态求解器采用变时间步长的求解方法,其所得数据为非等间距数据,所以通过插值法可将该数据转换为定周期的采样数据,然后通过傅里叶变换得到各周期信号的频率与相位特性。表2为模型a的流场特征参数及其频率ω与相位φ特性。

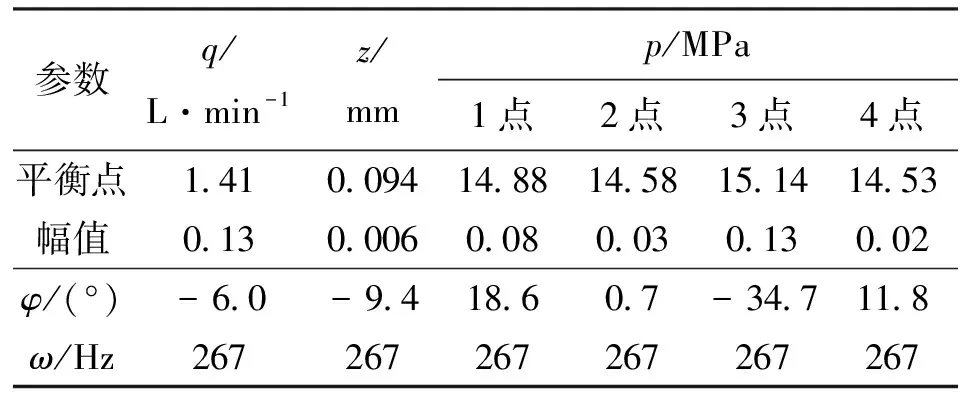
表2 模型a的流场特征参数及其频率与相位特性

根据表2中的数据,从平衡点压力来看,1点压力高于2、4点压力,低于3点压力,这是由于阻尼孔中的射流冲击阀芯表面后的一部分动能转化为静压能,使3点所在区域的压力升高(见图5);从压力幅值来看,3点压力幅值大于1点,幅值比可达1.625,这是由于阀芯运动致使射流产生的动压发生了较大波动,3点的压力变化滞后于阀芯位移和进口压力,相对于阀芯位移的最大滞后相位角达25.3°,相对于进口压力的最大滞后相位角达53.3°。

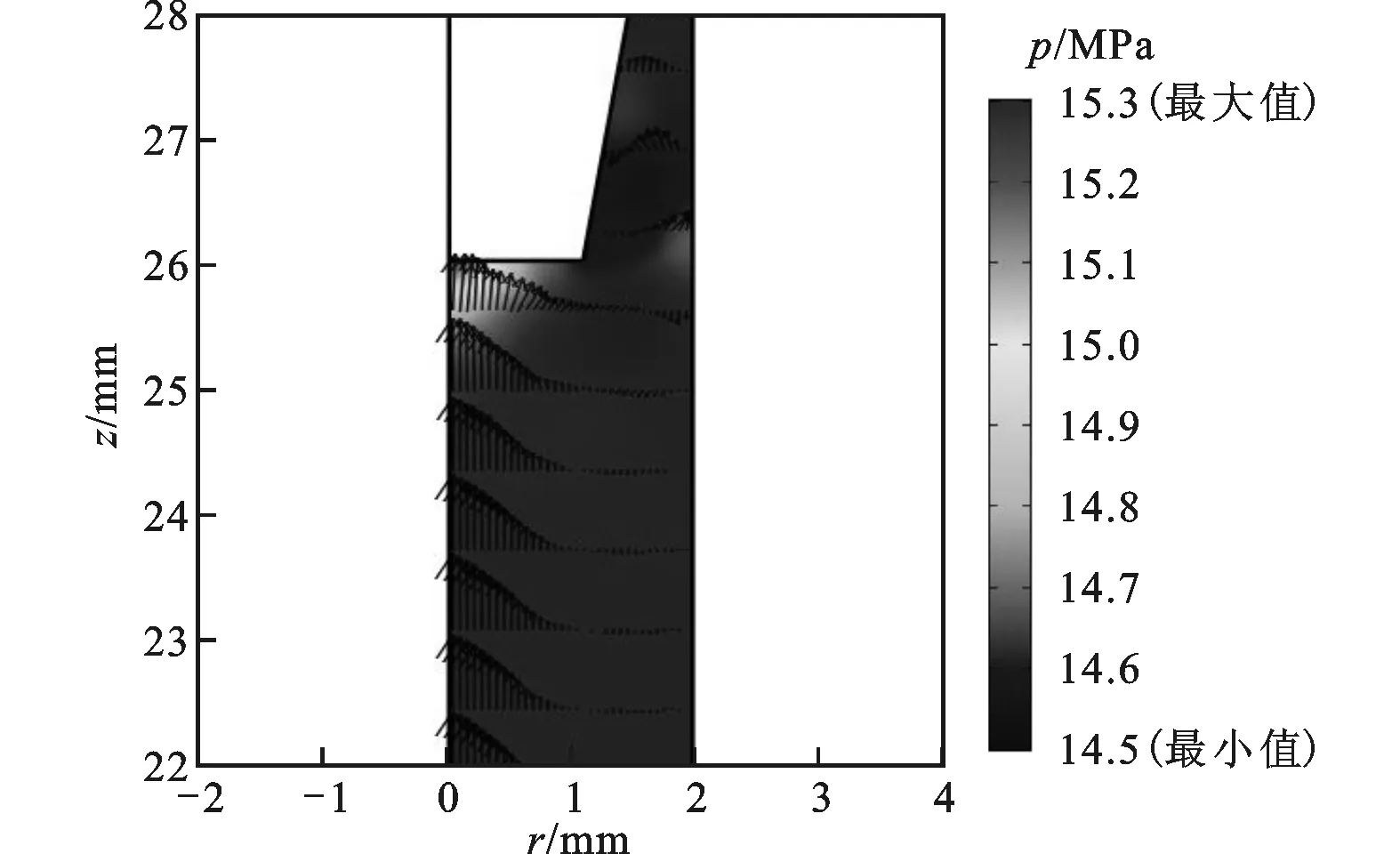
图5 t=8 ms时模型a在阀口前端的流场速度矢量和阀芯表面的压力分布

t=8 ms时模型a在阀口前端的流场速度矢量和阀芯表面的压力分布如图5所示。图中平行于对称轴的箭头表示阻尼孔中流出的淹没射流,作用在阀芯顶端的一个圆形区域,该区域的压力明显升高,且压力的相位滞后于阀芯位移的相位,本文将此区域称为射流冲击区。模型a中射流冲击区为阀芯前端平面r<0.8 mm的区域,在射流冲击区中随着r的增大,冲击作用逐渐减弱,压力及其幅值逐渐降低,压力相对于阀芯位移的相位滞后角逐渐减小(见图3和图6)。除阀口前端射流冲击区以外的阀芯表面(包括阀芯锥面)称为静压区,该区域的压力相位角超前于阀芯位移相位角(见图6)。

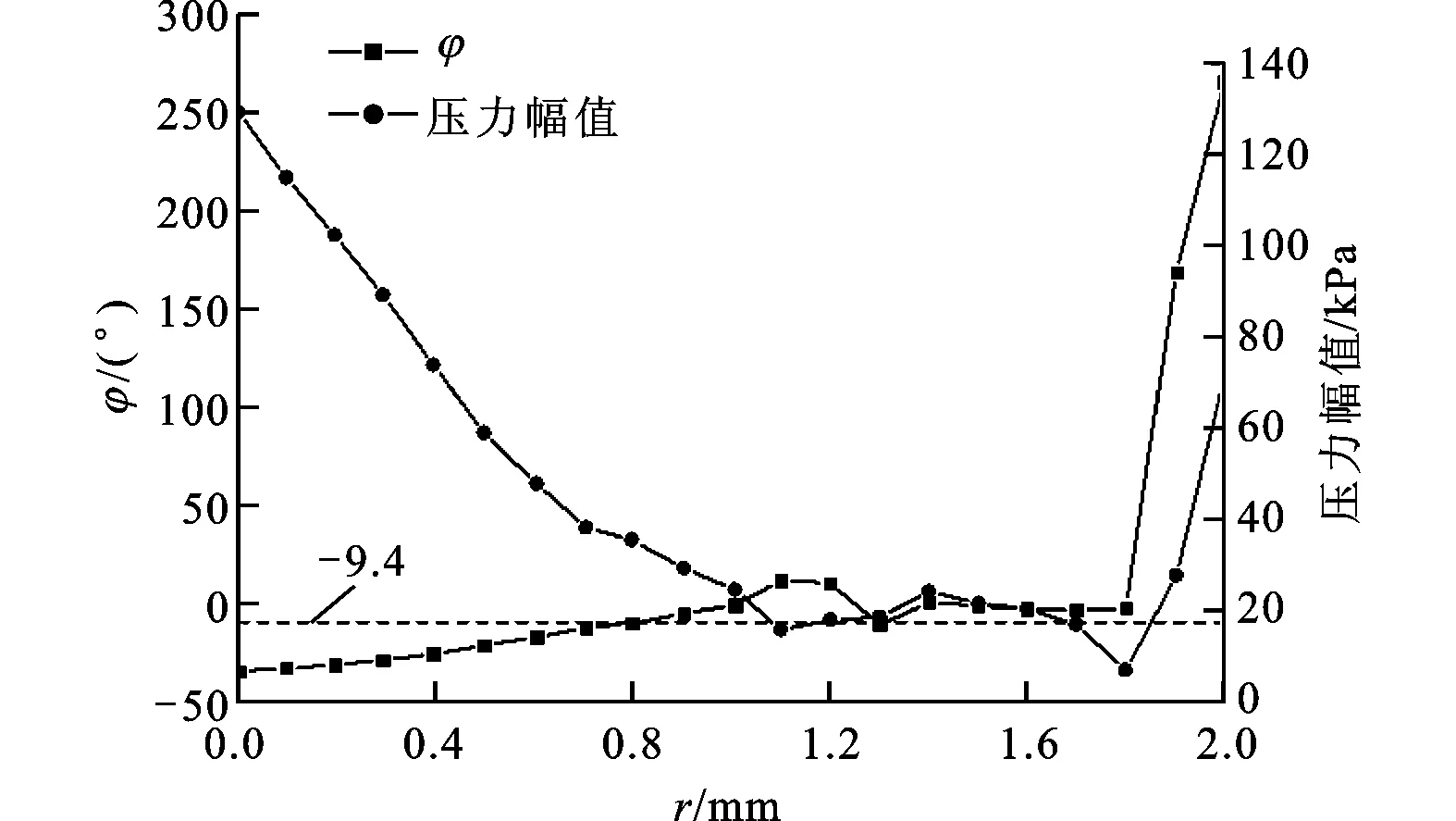
图6 模型a阀口前端阀芯表面的压力相位角与压力幅值变化

采用同样的方法可得到模型b、c的流场特征参数及频率特性,如表3、4所示。

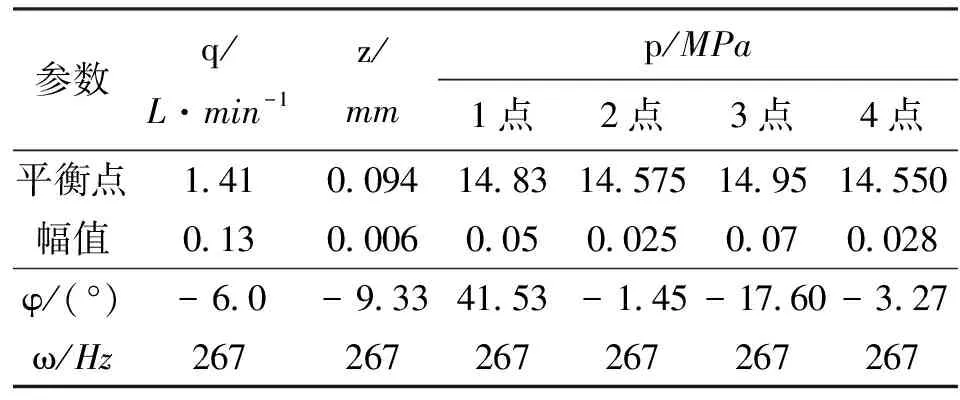
表3 模型b的流场特征参数及其频率与相位特性

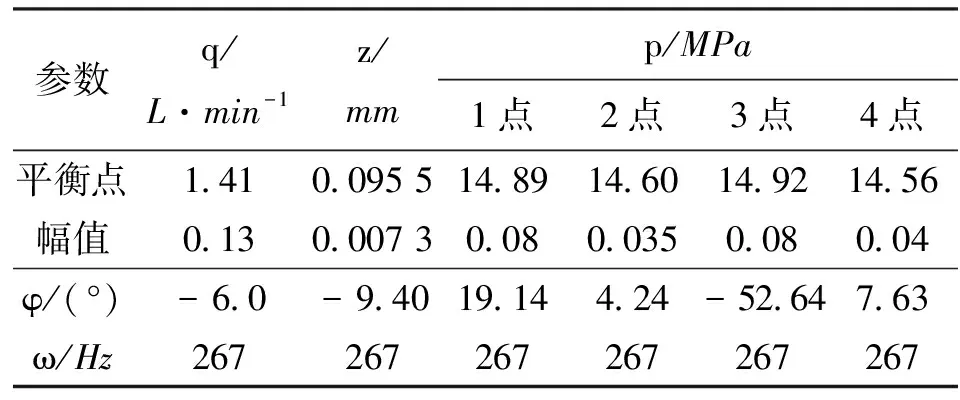
表4 模型c的流场特征参数及其频率与相位特性

比较表2、3中的动态特性和图3中的稳态压力分布可知,虽然模型b的阀腔体积相对模型a增大了一倍,但由于射流冲击长度不变,所以图3中阀口前端阀芯表面的压力分布与图1中阀芯位移阶跃响应曲线基本相同,且表2、3中阀芯位移平衡点均为0.094 mm,位移幅值均为0.006 mm。因此,当射流冲击长度不变,阀口前端至阻尼孔之间的容腔体积增加一倍时,压力调节阀的静、动态特性并不会发生明显变化。

比较表2、4中的动态特性和图3中的稳态压力分布可知:由于模型c中射流冲击长度比模型a增加了一倍,阻尼孔淹没射流中液压油的掺混作用增强,所以图3中模型c的阀芯表面的压力分布更加平缓,整个阀口前端阀芯表面的压力略有增加,使得稳态时模型c的阀芯位移增大了3.6%(见图2);与瞬态时模型a相比,模型c射流冲击区压力相对于阀芯位移的相位滞后角增大,但射流冲击区的压力幅值减小,射流冲击区的面积增大,模型c中射流冲击区为r<0.86 mm的区域(见图7)。

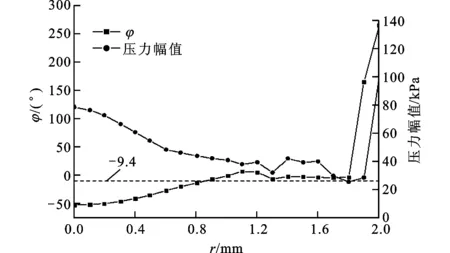
图7 模型c阀口前端阀芯表面的压力相位角与压力幅值变化

2.2.2 阀口前端阀芯表面的液压作用力 对阀口前端阀芯表面射流冲击区和静压区的压力分别进行积分,得到阻尼孔扰动射流作用下阀口前腔阀芯表面的液压作用力,如图8、9所示。

图8中射流冲击区液压力的相位为-21.58°,滞后于阀芯位移;静压区液压力的相位为141.84°,超前于阀芯位移。两区域液压力的相位差为163.42°,近似于反相位,两区域液压力叠加后使得阀口前端阀芯表面的液压力幅值大大减小。图9中射流冲击区液压力的相位为-31.02°,静压区液压力的相位为64.23°。相位差为95.25°时,两区域液压力叠加后使得阀口前端阀芯表面的液压力幅值略有增大。从表2、4中的阀芯位移幅值来看,模型c的阀芯位移幅值相比模型a增大了21.7%,即在相同的流量脉动下,当静压区与射流冲击区的液压力得到补偿时,阀芯的轴向振动幅值大大减小,阀芯轴向运动的稳定性得以提高,文献[11]的实验结果也证明了模型a的稳定性优于模型c。

从图8、9中看出,阀口前端阀芯表面的液压力幅值主要取决于射流冲击区与静压区液压力的相位关系。因此,要减小扰动射流作用下阀芯的轴向振动幅值,可合理配置射流冲击区和静压区液压力的相位和幅值,通过静压区液压力补偿射流冲击区液压力,可提高压力调节阀的轴向运动稳定性。

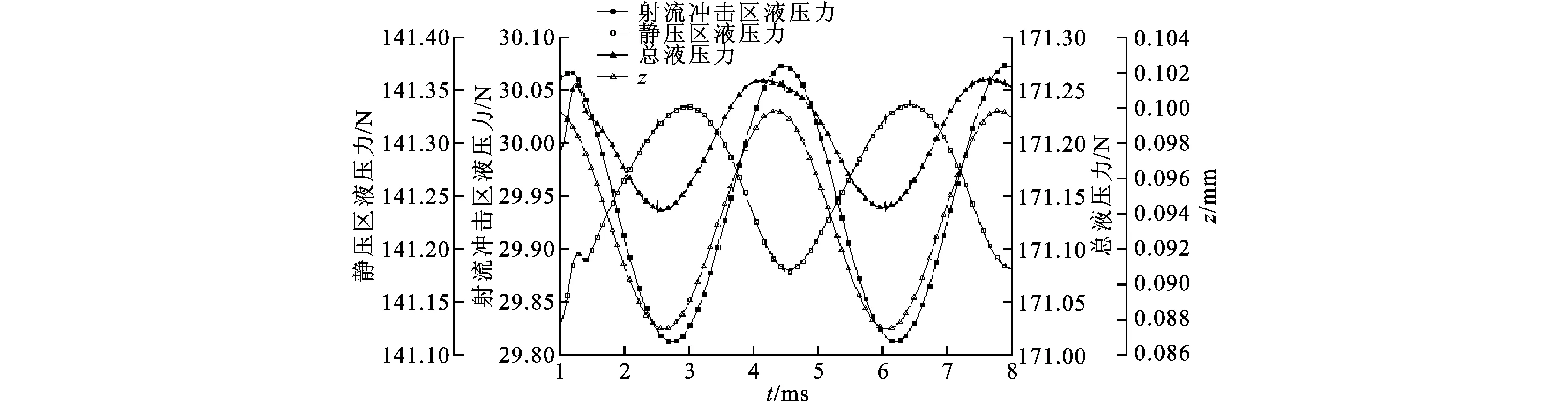
图8 模型a阀口前端阀芯表面的液压作用力

图9 模型c阀口前端阀芯表面的液压作用力

3 结 论

在不同阀腔结构下,通过对带阻尼孔的压力调节阀进行流-固耦合计算,运用分布式参数的相位分析方法,可得出如下结论。

(1)带阻尼孔的压力调节阀的阀口前端阀芯表面可分为射流冲击区和静压区两部分。两区域的面积及压力的相位和幅值均与射流冲击长度密切相关。

(2)阀芯的轴向振动幅值主要取决于射流冲击区与静压区液压力的相位差。当射流冲击区与静压区液压力的相位差趋于180°时,阀芯的轴向振动幅值减小,阀芯轴向运动的稳定性提高。

(3)带阻尼孔的压力调节阀的静、动态特性与阀口前腔容积大小基本无关。当射流冲击长度不变,阀腔容积增加一倍时,阀芯振动幅值基本不变,这与文献[8]的实验结论一致。

[1] 任玉婷.浅析溢流阀高频噪声的产生原因及其控制 [J].液压与气动,2001,7: 34-35.

REN Yuting.On reason and control high-frequency noise of the relief valve [J].Chinese Hydraulics & Pneumatics,2001,7: 34-35.

[2] OSHIMA S,ICHIKAWA T.Cavitation phenomena and performance of oil hydraulic poppet valve: 1st report Mechanism of generation of cavitation and flow performance [J].Bulletin of JSME,1985,28(244): 2264-2271.

[3] 贺小峰,何海洋,刘银水,等.先导式水压溢流阀动态特性的仿真 [J].机械工程学报,2006,42(1): 75-80.

HE Xiaofeng,HE Haiyang,LIU Yinshui,et al.Numerical simulation on the dynamic characteristics of a two-stage water hydraulic relief valve [J].Chinese Journal of Mechanical Engineering,2006,42(1): 75-80.

[4] 张康智,陈加胜.纯水溢流阀的工作稳定性研究 [J].机床与液压,2007,35(9): 165-167.

ZHANG Kangzhi,CHEN Jiasheng.The research on operation stability of the water hydraulic relief valve [J].Machine Tool & Hydraulics,2007,35(9): 165-167.

[5] TSUKIJI T,SUZUKI Y.Numerical simulation of an unsteady axisymmetric flow in a poppet valve using a vortex method [C]∥Proceedings of ESAIM.Les Ulis Cedex A,France: EDP Sciences,1996: 415-427.

[6] ERHARD M,KIREEV V,BONANNO A,et al.Simulation-based design of a direct-operated proportional pressure relief valve[C/CD]∥8th International Fluid Power Conference.Dresden,Germany: Institute of Fluid Power,2012: Group A1

[7] STAORU HAYASHI.Instability of poppet valve circuit [J].JSME International Journal,1995,38(3): 357-366.

[8] WANDLING D E,JOHNSON B L.Hydraulic poppet valve stability [J].SAE Trans,1972,81(4): 2358.

[9] KASAI K.On the stability of a poppet valve with an elastic support: 1st report Considering the effect of the inlet piping system [J].Bulletin of JSME,1968,48(11): 1068-1083.

[10]KASAI K.On the stability of a poppet valve with an elastic support: 2nd report Considering the effect of the outlet piping system [J].Bulletin of JSME,1968,48(11): 1084-1103.

[11]JORGENSEN J E.Dynamic stability of hydraulic poppet valves [D].Cambridge,MA,USA: Massachusetts Institute of Technology,1963.

[本刊相关文献链接]

史文库,毛阳,姜雪,等.发动机半主动液压悬置的动态特性及参数影响分析.2014,48(1):42-47.[doi:10.7652/xjtuxb 201401008]

于立娟,王小东,张学成.轴向柱塞泵流量脉动主动控制方法及仿真研究.2013,47(11):43-47.[doi:10.7652/xjtuxb2013 11008]

章云,梅雪松,胡振邦,等.注液式高速切削主轴动平衡装置设计及其性能研究.2013,47(3):13-17.[doi:10.7652/xjtuxb201303003]

王健健,张建富,冯平法,等.楔式动力卡盘静态夹持精度建模与综合.2013,47(3):90-95.[doi:10.7652/xjtuxb201303 017]

沈楚敬,苑士华,魏超,等.液压压紧式牵引传动装置传动效率研究.2012,46(7):32-37.[doi:10.7652/xjtuxb201207007]

张慧贤,寇子明,吴娟,等.液压激波作用下管道流固耦合的动力学建模.2012,46(3):94-99.[doi:10.7652/xjtuxb2012 03017]

于安才,姜继海.液压混合动力挖掘机回转装置控制方式的研究.2011,45(7):30-33.[doi:10.7652/xjtuxb201107006]

卢为,成永红,王增彬,等.环氧及其复合材料在变压器油中的快脉冲闪络特性.2010,44(10):83-87.[doi:10.7652/xjtuxb201010016]

任燕,阮健,贾文昂.2D阀控电液激振器偏置控制的特性分析.2010,44(9):82-86.[doi:10.7652/xjtuxb201009017]

华成,张庆,徐光华,等.具有小世界特性的复杂液压系统故障源搜索方法.2010,44(7):79-84.[doi:10.7652/xjtuxb 201007018]

江小霞.三向地震模拟平台控制系统的研究.2009,43(10):16-21.[doi:10.7652/xjtuxb200910004]

魏树国,赵升吨,张立军,等.直驱泵控式液压机液压系统的动态特性仿真及优化.2009,43(7):79-82.[doi:10.7652/xjtuxb200907017]

(编辑 苗凌)

OrificeJetResponseCharactersinPressureRegulatingValve

MIN Wei1,2,JI Hong1,2,WANG Zhengrong1,2,WANG Jinlin1,2

(1.School of Energy and Power Engineering,Lanzhou University of Technology,Lanzhou 730050,China;2.Hydraulic & Pneumatic Engineering Research Center in Gansu Province,Lanzhou 730050,China)

To reveal the stability essence of pressure regulating valve with orifice,the response process of a poppet under the action of step and periodic excitation signal was simulated with fluid structure interaction algorithm.The axial vibration character of the poppet,the surface pressure distribution and varying rule of the poppet in front of valve port of different valve chamber structures were analyzed.It is found that the jet shock to the poppet divides poppet surface in front of valve port into jet impingement area and static pressure area,the vibration amplitude of the poppet depends on phase difference of the fluid force in jet impingement area and static pressure area,and is greatly reduced while the phase difference approaches to 180°.

pressure regulating valve; orifice jet; fluid structure interaction; axial vibration;stability mechanism

2013-07-08。

闵为(1978—),男,博士生;冀宏(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51075194);甘肃省自然科学基金资助项目(1112RJ2A026)。

时间:2014-04-03

10.7652/xjtuxb201406014

TH137.52

:A

:0253-987X(2014)06-0080-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140403.1516.001.html